
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еліптичні орбіти в атомі водню і їх квантування
При русі електрона по колу змінюється тільки одна координата – азимут φ або пройдений шлях
(1.33)
Рис. 1.11 Залежність υта r представлена графіком, тут же на осях υта r відмічені квантові значення υта r, одержувані згідно теорії Бора для атома водню з урахуванням його другого і третього постулату, коли
Отже квантові умови другого постулату Бору
виділяють з неперервної нескінченої множини можливих колових орбіт руху електрона дискретну нескінченну множину. Проте електрон може рухатися не тільки по колу, але і по еліптичній орбіті, в одному з фокусів якої буде ядро (1-й закон Кеплера). В цьому випадку змінними є два параметри - азимут φ і відстань електрона до ядра – r (тобто дві степені свободи), а траєкторія руху характеризується двома постійними параметрами - малою (b) і великою (a) піввісями еліпса, які згідно класичній механіці можуть приймати будь-які значення: 0 < b < ∞ та 0 < а < ∞.
Отже, сукупність можливих рухів - двояко-нескінченна неперервна множина. При цьому класична механіка вимагає виконання двох законів Кеплера
Чи можна узагальнити другий постулат Бора і проквантувати еліптичні орбіти електрона в одноелектронних системах, тобто виділити з двояко-нескінченної неперервної множини деяку двояко-нескінченну, але дискретну множину? Однієї квантової умови недостатньо, дійсно, спробуємо використати лише умову, що
Цій умові задовольняє різноманіття орбіт, для яких (1.38) встановлює тільки залежні від п зв'язки між а і b еліпса, тобто b = fn(a), але величина а може бути довільною. Тобто в системі з f степенями свободи квантування вимагає f квантових умов. Опишемо таку систему узагальненими координатами gi і узагальненими імпульсами pi, де (і = 1,2,3... f). Якщо позначити К (gі, ġі) - кінетичну енергію, тоді
Умова квантування атома по Зоммерфельду вимагає, щоб інтеграли рухів(величини, не змінні з часом) для стаціонарних квантових рухів мали дискретні значення, кратні постійній Планка
інтегрування в межах (від 0 до 2π або від min до max). Коло на інтегралі означає, що інтегрування по координаті gі треба проводити по всьому циклу її зміні.
Вираз (2-39) і виділяє з неперервної нескінченої множини рухів, можливих по класичній механіці, деяку дискретну множину. Наприклад, для колового руху єдиною узагальненою координатою буде азимут φ; g1 = φ, тоді кінетична енергія через узагальнену швидкість
тобто просто момент кількості руху, який повинен бути квантований, умова Зоммерфельда запишеться у вигляді:
але згідно другому закону Кеплера mrv = const, тоді (2-40) має вигляд:
Виходить, що другий постулат Бору є окремий випадок застосування умов квантування Зоммерфельда. При русі електрона по еліптичній орбіті за узагальнені координати треба взяти r і φ. Тоді його повна кінетична енергія має значення
тоді умови Зоммерфельда запишуться:
Де nr та nφ радіальні та азимутальні квантові числа. Враховуючи, що mrυ=const маємо:
Тобто, як і для руху по колу, але тут rn = rn(t) і vn=vn(t). (1.43) визначає момент кількості руху електрона в атомі. Використовуючи рівняння (1.41) і (1.42) з врахуванням законів Кеплера можна визначити значення великих та малих піввісей еліпса та повну енергію системи Enφ,nr, які відповідають певним парам значень nφ nr. Дані величини мають вигляд:
Тут Враховуючи, що a
При b=0 - еліпс вироджується в пряму, яка проходить через ядро,що неможливо. Отже,
В рівняння входить сума n=1,2,3… k=1,2,3…n, але
З врахуванням позначень n і k для a, b і E маємо:
Розглянемо можливі орбіти руху електрона, для певних значень головного квантового числа, в залежності від величини азимутального квантового числа квантового числа k, наведені в таблиці 2. Таблиця 2.
Форми траєкторій руху відповідні значенню =3 і =1, 2, 3 наведені на рис.
Рис. 1.12 А діаграма енергетичних рівнів для одноелектронної системи буде мати наступний вигляд:
Рис.1.13 Стани з різним k позначаються: S, P, D, F… Із діаграми видно, що хоча число квантових типів руху електрона зросло, але число рівнів енергії залишилось, а це зрозуміло з (2.50), адже Слід відмітити, що є рух при якому періоди зміни координат r і 1. Електрон рухається в чисто Кулонівському полі, коли 2. При постійній масі електрона. Але з врахуванням залежності маси електрона від швидкості розрахунки Зоммерфельда показали, що періоди зміни r і Тоді для значення енергії атома в даному стані зі значенням квантових чисел
де По (1.51)
Рис. 1.14 Отже, перша лінія Бальмера повинна складатися з групи шести близько розташованих ліній, але в експерименті завжди спостерігається менше ліній. Аналіз спектрів показав, що в них є тільки ті лінії, які відповідають переходам між рівнями, для яких виконується умова:
Всі решта переходів малоймовірні. Тоді для першої лінії Бальмера залишаться тільки три лінії, які відповідають переходам:
1). 2). 3). Правило переходів між рівнями яке визначається виразом (1.52) і називається правилом добору.
Просторове квантування Рух електрона в просторі і його положення характеризується трьома координатами, і є рухом з трьома степенями вільності. В сферичній системі координат (
Тут
Рис. 1.15
Тут Якщо на систему не діють зовнішні сили, то орбіта руху електрона буде нерухомою і плоскою. Визначимо величини інтегралів руху, які входять в рівняння (2.54). Вираз для кінетичної енергії має вигляд (для сферичної системи координат):
А повна енергія буде як сума кінетичної і потенціальної:
Тоді для величин імпульсів маємо:
Враховуючи, що без дії зовнішніх сил, повна енергія системи визначається головним квантовим числом, то отримаємо: n=nr+nθ+nψ=nr+nφ (1.58) nθ+nψ=nφ В вираз повної енергії системи координата
Тоді на основі третьої умови квантування в (1.54) маємо:
Величина Враховуючи, що
тобто
Накладання магнітного поля знімає виродження по
Рис.1.16
Магнетон Бора Електрон, що рухається по орбіті, еквівалентний контуру зі струмом. Сила цього струму і рівна заряду електрона е, помноженому на число його обертів в 1 секунду
А площа, охоплена струмом і, рівна площі еліпса S. Для моменту кількості руху
Звідси Але за другим законом Кеплера секторіальна швидкість Тоді:
Магнітний момент контуру зі струмом дорівнює: Підставляючи отримані значення i та S маємо:
Це магнетон Бора – елементарний магнітний момент. Магнітні моменти атомів, обумовлені орбітальним рухом електрона, повинні бути кратні елементарному магнітному моменту. Для перевірки висновків теорії просторового квантування і експериментального визначення величини магнетона Бора був проведений дослід Штерна і Герлаха (1922р.).
Рис. 1.17 Ідея досліду. Якщо в неоднорідному магнітному полі напрямленому по осі х, розміщений магнітний диполь довжиною l, вісь якого утворює кут
Де
Цей вираз буде справедливий і тоді, коли магнітний момент створюється не тільки «магнітними масами», а і струмом, який протікає по контуру, чи рухом електрона по орбіті атома.
Схема пристрою наступна. У вакуумному балоні з пічки п випаровувалися атоми срібла. Частина атомів пролітала через діафрагми D1 і D2 без зіткнень по прямій лінії, далі через магнітне поле. Якщо поля немає, то вони конденсуються вузькою смужкою на пластинці М ( випадок а згідно рис1.18 .). При наявності поля (неоднорідного) відбувалося відхилення атомного пучка. Згідно класичним уявленням відхилення будуть любі по (1.67), де Рис.1.18 (випадок б).
Рис.1.19 По квантовій теорії площини орбіт атомів срібла, основним станом яких є S – стан, якому відповідає K=1, можуть орієнтуватися по відношенню до напрямку магнітного поля тільки трьома способами (m=-1;0;+1) і відповідно пучок повинен розпадатися на три окремих (випадок в). Експеримент дав тільки дві (випадок г) смужки, середньої смужки не було. Але наявність цих двох смужок чітко підтвердила правильність висновків теорії просторового квантування. Виміривши величину
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.42 (0.059 с.) |
 , тобто є одна ступінь свободи. Такий рух характеризується одним постійним параметром - радіусом r = const, який в класичній механіці може мати будь-яке значення 0 < r < ∞, відповідно будь-яке значення можуть мати інші параметри, що характеризують рух (енергія Е, момент кількості руху і т.д.) Встановлена раніше умова механічної стійкості (
, тобто є одна ступінь свободи. Такий рух характеризується одним постійним параметром - радіусом r = const, який в класичній механіці може мати будь-яке значення 0 < r < ∞, відповідно будь-яке значення можуть мати інші параметри, що характеризують рух (енергія Е, момент кількості руху і т.д.) Встановлена раніше умова механічної стійкості ( ) дає тільки певний зв'язок між різними параметрами:
) дає тільки певний зв'язок між різними параметрами:

 (1.34)
(1.34) (1.35)
(1.35) (1.36)
(1.36) (1.37)
(1.37)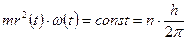 (1.38)
(1.38) , тут
, тут  =
=  - узагальнена швидкість.
- узагальнена швидкість. (1.39)
(1.39) = 0, ± 1; ± 2…
= 0, ± 1; ± 2…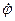 приймає значення
приймає значення  , а спряженний з координатою узагальнений імпульс буде
, а спряженний з координатою узагальнений імпульс буде ,
, (1.40)
(1.40) або
або 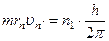 , де
, де  = 1,2,3…
= 1,2,3… , а спряжені імпульси будуть визначатись як
, а спряжені імпульси будуть визначатись як і
і 
 (1.41)
(1.41) (1.42)
(1.42) (1.43)
(1.43) (1.44)
(1.44) (1.45)
(1.45) (1.46)
(1.46) - радіус першої Боровської колової орбіти і Ui – іонізаційний потенціал даної системи.
- радіус першої Боровської колової орбіти і Ui – іонізаційний потенціал даної системи. b, то з (1.44) і (1.45) випливає, що
b, то з (1.44) і (1.45) випливає, що 
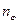 або
або 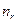
 = n – головне квантове число, а азимутальне число
= n – головне квантове число, а азимутальне число  (1.49)
(1.49) ;
;  ;
;  (1.50)
(1.50)
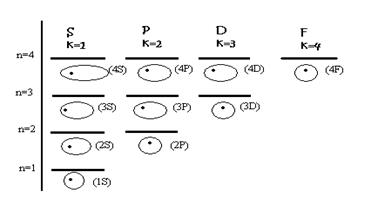
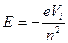 і не залежить від азимутального числа
і не залежить від азимутального числа  однакові, тобто еліпс нерухомий в просторі, як показав Зоммерфельд це можливо при виконанні двох умов:
однакові, тобто еліпс нерухомий в просторі, як показав Зоммерфельд це можливо при виконанні двох умов: ≈
≈  .
. , (1.51)
, (1.51) - постійна тонкої структури
- постійна тонкої структури залежить від n і k, тобто виродження по азимутальному квантовому числу вже ліквідовано. Але така ліквідація виродження має приводити до ускладнення спектра випромінювання атома водню, так як одному енергетичному рівню з головним квантовим числом n будуть відповідати різні енергії, які визначаються різними значеннями
залежить від n і k, тобто виродження по азимутальному квантовому числу вже ліквідовано. Але така ліквідація виродження має приводити до ускладнення спектра випромінювання атома водню, так як одному енергетичному рівню з головним квантовим числом n будуть відповідати різні енергії, які визначаються різними значеннями 
 (1.52),
(1.52), ,
,  ,
,  ) відповідно до умов Зоммерфельда ми отримаємо три рівняння, які описуватимуть рух з трьома степенями вільності:
) відповідно до умов Зоммерфельда ми отримаємо три рівняння, які описуватимуть рух з трьома степенями вільності:
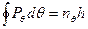
 (1.54)
(1.54) - екваторіальне квантове число
- екваторіальне квантове число - широтне квантове число
- широтне квантове число
 з площиною (XOY).
з площиною (XOY). (1.55)
(1.55) (1.56)
(1.56) (1.57)
(1.57) або
або 
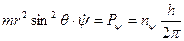 (1.59)
(1.59)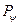 являє собою проекцію повного моменту кількості руху електрона
являє собою проекцію повного моменту кількості руху електрона  на вісь Z. Позначимо
на вісь Z. Позначимо  , тоді
, тоді  ;
; 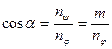
 та nθ+nψ=nφ, то значення квантового числа
та nθ+nψ=nφ, то значення квантового числа 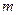 може бути в межах:
може бути в межах:
 (1.60)
(1.60)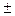 1;
1; 


 (1.61)
(1.61) , який може бути визначений добутком маси електрона на подвоєну секторну швидкість
, який може бути визначений добутком маси електрона на подвоєну секторну швидкість  , повинна виконуватись умова:
, повинна виконуватись умова: (1.62)
(1.62) , К – азимут кв. число.
, К – азимут кв. число. =const =
=const =  ,
, (1.63)
(1.63)
 (1.64), (1.65)
(1.64), (1.65)
 (1.66)
(1.66) - величина «магнітної маси», яка зосереджена на кожному з полюсів диполя, але
- величина «магнітної маси», яка зосереджена на кожному з полюсів диполя, але  , і тоді заміняючи
, і тоді заміняючи  маємо:
маємо: (1.67)
(1.67)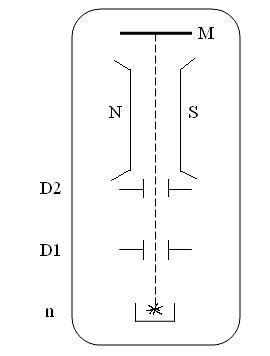 Отже, якщо пропускати через таке неоднорідне поле атоми речовини, то вони повинні відхилятися від напрямку свого початкового руху, і це відхилення буде проходити по різним закономірностям з точки зору класичних і квантових уявлень.
Отже, якщо пропускати через таке неоднорідне поле атоми речовини, то вони повинні відхилятися від напрямку свого початкового руху, і це відхилення буде проходити по різним закономірностям з точки зору класичних і квантових уявлень. , тобто на пластинці повинна бути розмита широка смужка (суцільна і неперервна)
, тобто на пластинці повинна бути розмита широка смужка (суцільна і неперервна)
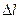 відхилення, знаючи
відхилення, знаючи  і геометрію пристрою, υ та m атомів можна вирахувати
і геометрію пристрою, υ та m атомів можна вирахувати  .
.


