
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предикаты и логические операции над ними
Для формализации естественного языка часто недостаточно высказываний. Это хорошо видно на таком классическом примере.
Каждый человек смертен. Так как Сократ человек, то он смертен». Это утверждение можно представить формулой алгебры высказываний
где
Построим таблицу истинности этой формулы:
Отсюда вывод: формула алгебры высказываний не общезначимая, а значить высказывание Таким образом, необходимо было усовершенствовать логику высказываний, что и привело к созданию алгебры предикатов. Дадим определение предиката. Пусть
называется одноместным предикатом и обозначается Так как, отображение можно рассматривать как функцию, то одноместный предикат можно рассматривать как произвольную функцию с областью определения Множество Множество
называется областью истинности предиката
Если Пусть множество
называется n-местным предикатом Количество аргументов предиката называется его порядком. Высказывания логики высказываний можно интерпретировать как 0-местные предикаты. Пример 1 1) Истинное высказывания «11 – простое число» – 0-местный предикат. 2) Утверждение « 3) Утверждение «Число Предметная область
Множество истинности предиката 4) Утверждение «
Так как предикаты могут принимать два значения Конъюнкцией двух предикатов
Дизъюнкцией предикатов
Отрицанием предиката
– разницей множеств Импликацией предикатов
Пример 2 На множестве
заданы предикаты Выполнение.
Пусть предикат Пример 3 На множестве Выполнение. Таблица истинности предикатов на множестве
Область истинности предиката Таблица истинности предикатов на множестве
Область истинности предиката Таблица истинности предикатов на множестве
Область истинности предиката Пример 4 Даны два двухместных предиката на множестве
Является ли один из предикатов логическим выводом другого? Выполнение. Область определения и область истинности предиката
Рис 1.1. Область определения и область истинности предиката Область определения и область истинности предиката
Рис.1.2. Область определения и область истинности предиката Видно, что КВАНТОРНЫЕ ОПЕРАЦИИ Пусть Высказывание Кванторы Пример 1 Пусть на множестве
Пусть множество
Итак, кванторные операции Переменная Кванторные операции применяются и к многоместным предикатам. Применение кванторных операций к двухместному предикату К двухместным предикатам можно применять кванторные операции и по двум переменным. В результате получим восемь высказываний:
ФОРМУЛЫ АЛГЕБРЫ ПРЕДИКАТОВ Формулы алгебры предикатов строятся из атомарных формул (атомов). Для записи атомов алгебры предикатов используются: · символы истинностных значений ( · символы переменных высказываний ( · символы предметных переменных () · символы предметных констант (элементов предметной области); · символы предикатов; · функциональные символы; · символы логических операций; · символы кванторных операций; · вспомогательные символы: скобки, запятые. Аргументы n -местного предиката называются термами. Терм рекурсивно определяется следующим образом: · предметные переменные и предметные константы – термы; · если Формулой алгебры предикатов называют любое выражение, содержащее символику 1-7 и удовлетворяющее таким условиям:
· атом – формула; · если · если · если Все предметные переменные атомных формул свободны. Следовательно, всякая формула алгебры высказываний есть также формула алгебры предикатов. Пусть Подслово формулы В алгебре предикатов под интерпретацией понимают присвоение атомам истинностных значений. В логике предикатов интерпретация формул имеет расширенный смысл. Интерпретация формулы После уточнения интерпретации в логике предикатов, такие понятия как общезначимость, противоречивость, осуществимость, нейтральность (не общезначимость) формул и логическое следствие могут быть определены так же, как и в алгебре предикатов. Пример 1 Которые из приведенных ниже слов являются формулами алгебры предикатов? 1) 2) 3) Выполнение. 1) 2. 3. Пример 2 Пусть двухместный предикат
· · · · Вычислить значения формул алгебры предикатов: a) b) Выполнение. a) o o В итоге:
(число
o o o Число
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.219.217 (0.089 с.) |
 ,
, : «Каждый человек смертен»,
: «Каждый человек смертен»,  : «Сократ – человек»,
: «Сократ – человек»,  : «Сократ – смертен», или соответствующей формулой алгебры высказываний
: «Сократ – смертен», или соответствующей формулой алгебры высказываний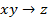 .
. .
.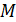 – произвольное множество. Отображение
– произвольное множество. Отображение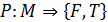
 ,
, 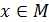 .
. и областью значений
и областью значений  .
.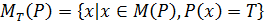
 .
. , то предикат
, то предикат  (пустому множеству) – тождественно ложный.
(пустому множеству) – тождественно ложный. . Отображение (функция)
. Отображение (функция) ,
, 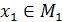 ,
,  , …,
, …,  .
. – простое число» – одноместный предикат
– простое число» – одноместный предикат 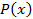 . Предметная область этого предиката – множество натуральных чисел (
. Предметная область этого предиката – множество натуральных чисел ( ).
). 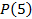 – истинное высказывание,
– истинное высказывание, 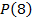 – ложное высказывание. Область истинности этого предиката – множество простых чисел:
– ложное высказывание. Область истинности этого предиката – множество простых чисел:  .
. больше числа
больше числа  » – двухместный предикат
» – двухместный предикат  .
. .
. – одноместный предикат, определен на множестве
– одноместный предикат, определен на множестве  (тождественно ложный предикат).
(тождественно ложный предикат).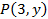 – одноместный предикат, определен на множестве
– одноместный предикат, определен на множестве  .
. – ложное высказывание (0-местный предикат).
– ложное высказывание (0-местный предикат). .
. » – одноместный предикат
» – одноместный предикат  – множество корней квадратного уравнения. ∎
– множество корней квадратного уравнения. ∎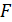 и
и  , то над ними можно выполнять все логические операции логики высказываний.
, то над ними можно выполнять все логические операции логики высказываний. , определенных на множестве
, определенных на множестве  , называют предикат
, называют предикат  с областью истинности
с областью истинности
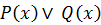 с множеством истинности
с множеством истинности
 с областью истинности
с областью истинности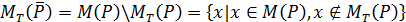
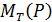 (дополнение множества
(дополнение множества  с областью истинности
с областью истинности .
.
 «
« «
«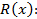 «
« : «
: « ,
,  ,
, 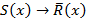 .
. ,
,  ,
, ,
,  .
. ,
, .
. ,
, ,
, ,
, ,
,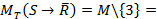
 . ∎
. ∎ . Предикат
. Предикат  . Предикаты
. Предикаты  ), если
), если 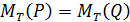 .
. определены два предиката:
определены два предиката:  : «
: « и
и  ?
? :
:

 , область истинности предиката
, область истинности предиката  . Эти области совпадают и поэтому предикаты на множестве
. Эти области совпадают и поэтому предикаты на множестве 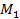 :
: , область истинности предиката
, область истинности предиката  . Эти области не совпадают и поэтому предикаты на множестве
. Эти области не совпадают и поэтому предикаты на множестве  , то
, то  :
: , область истинности предиката
, область истинности предиката  . Эти области не совпадают и поэтому предикаты на множестве
. Эти области не совпадают и поэтому предикаты на множестве  , то
, то 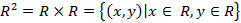 (
( – множество действительных чисел):
– множество действительных чисел): »,
»,  : «
: « ».
». (на рис.1.1 – заштрихованая),
(на рис.1.1 – заштрихованая), (на рис.1.2 – жирная линия)
(на рис.1.2 – жирная линия)

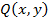 (рис. 1.2):
(рис. 1.2): ,
,
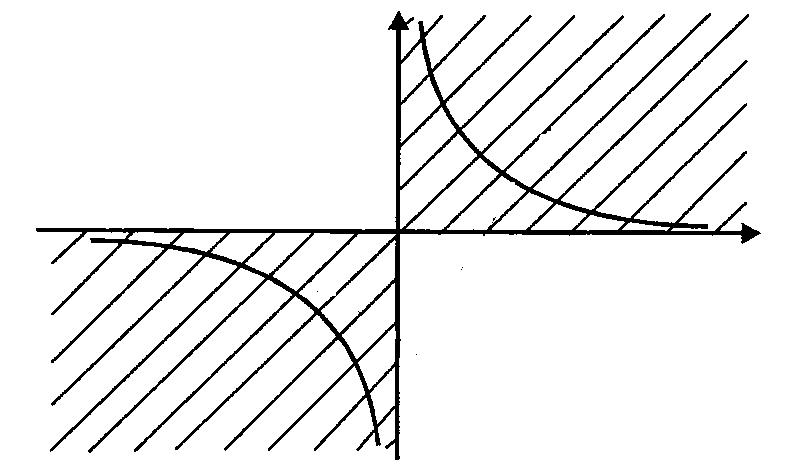
 , то есть
, то есть  – это высказывание, которое истинно, если предикат
– это высказывание, которое истинно, если предикат 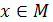 предикат
предикат  – истинный предикат (
– истинный предикат ( )». Знак
)». Знак  называется квантором всеобщности.
называется квантором всеобщности. – это высказывание, которое истинно, если существует такое
– это высказывание, которое истинно, если существует такое  называется квантором существования.
называется квантором существования. определены предикаты
определены предикаты  ложно;
ложно;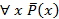 ложно;
ложно; истинно;
истинно; истинно;
истинно;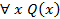 ложно;
ложно; истинно. ∎
истинно. ∎ конечно. Тогда
конечно. Тогда

 предиката
предиката 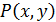 по переменной
по переменной 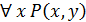 или
или  , который зависит от
, который зависит от 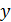 , и не зависит от
, и не зависит от 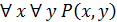 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; …);
…); -местный предикат и
-местный предикат и  – термы, то
– термы, то  также терм.
также терм. и
и  – формулы, то
– формулы, то  ,
, 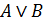 ,
,  тоже формулы при условии, что одна и та же предметная переменная не есть в
тоже формулы при условии, что одна и та же предметная переменная не есть в  – формула;
– формула;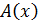 – формула, что содержит предметную переменную
– формула, что содержит предметную переменную  и
и 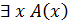 – формулы, причем, если в
– формулы, причем, если в  или
или  .
. ;
; ;
; ;
; не является формулой, потому что квантор существования
не является формулой, потому что квантор существования  употребляется для связанной переменной, что недопустимо;
употребляется для связанной переменной, что недопустимо; – символ переменной высказывания,
– символ переменной высказывания,  – символ логической операции,
– символ логической операции, 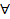 – символ кванторной операции,
– символ кванторной операции, 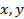 – символы предметных переменных,
– символы предметных переменных,  – предикатный символ, скобки и запятая – вспомогательные символы.
– предикатный символ, скобки и запятая – вспомогательные символы.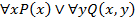 – не является формулой, потому что предметная переменная
– не является формулой, потому что предметная переменная  : «число n делится на число m». Предметная область этого предиката – область натуральных чисел. Тогда одноместный предикат:
: «число n делится на число m». Предметная область этого предиката – область натуральных чисел. Тогда одноместный предикат: : «число n делится на 3»;
: «число n делится на 3»; : «число n делится на 2»;
: «число n делится на 2»; : «число n делится на 4»;
: «число n делится на 4»; : «число n делится на 6»,
: «число n делится на 6»,  : «число n делится на 12».
: «число n делится на 12». ;
; .
. :
: : «Число n делится на 2 и на 3, то есть, делится на 6»;
: «Число n делится на 2 и на 3, то есть, делится на 6»; : «Если число n делится на 6, то оно делится на 12».
: «Если число n делится на 6, то оно делится на 12». ,
, делится на 6, но не делится на 12).
делится на 6, но не делится на 12). :
: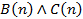 : «Число n делится на 2 и на 4, то есть, оно делится на 4»;
: «Число n делится на 2 и на 4, то есть, оно делится на 4»; : «Число n не делится на 6».
: «Число n не делится на 6». : «Если число n делится на 4, то оно не делится на 6».
: «Если число n делится на 4, то оно не делится на 6». делится на 4, но не делится на 6. Поэтому
делится на 4, но не делится на 6. Поэтому . ∎
. ∎


