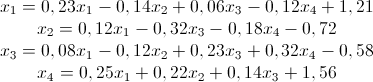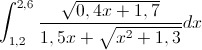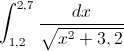Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
На тему «нахождение значения многочлена по схеме Горнера»Стр 1 из 4Следующая ⇒
Курсовая работа На тему «Нахождение значения многочлена по схеме Горнера»
Исполнитель Студент группы ЭМА-10 Каргаполов А.В. Руководитель Миронова Л.И.
Екатеринбург
Введение.. 4 1. Схема Горнера.. 5 1.1 Теоретическое описание схемы Горнера. 5 1.2 Пошаговый алгоритм нахождение значение многочлена по схеме Горнера. 7 1.3 Код программы, реализующей схему Горнера. 7 1.4 Описание контрольного примера. 8 1.5 Скриншот решения контрольного примера. 9 1.6 Описание примера №2. 10 1.7 Скриншот примера №2. 10 2. Презентационные материалы по методу «Схема Горнера». 11 3. Вычислительный практикум... 15 3.1 Отделение изолированных корней уравнения с помощью компьютерной программы 15 3.1.1 Пример №1. 15 3.1.2 Пример №2. 16 3.2 Уточнение корней с заданной точностью методом дихотомии. 17 3.2.1 Пример №1. 17 3.2.2 Пример №2. 18 3.3 Уточнение корней с заданной точностью методом хорд. 20 3.3.1 Пример №1. 20 3.3.2 Пример №2. 21 3.4 Уточнение корней с заданной точностью объединенным методом.. 23 3.4.1 Пример №1. 23 3.4.2 Пример №2. 24 3.5 Уточнение значения изолированного корня методом касательных. 26 3.5.1 Пример №1. 26 3.5.2 Пример №2. 27 3.6 Уточнение значения изолированного корня методом простых итераций. 29 3.6.1 Пример №1. 29 3.6.2 Пример №2. 30 3.7 Решение систем линейных уравнений методом Гаусса. 32 3.7.1 Пример №1. 32 3.8 Обращение матриц методом Гаусса. 33 3.8.1 Пример №1. 33 3.8.2 Пример №2. 34 3.9 Решение систем линейных уравнений методом простых итераций. 35 3.9.1 Пример №1. 35 3.9.2 Пример №2. 36 3.10 Интерполирование функций. 37 3.10.1 Пример №1. 37 3.11 Численное интегрирование. 38 3.11.1 Формула левых прямоугольников. 38 Пример №1. 38 3.11.2 Формула правых прямоугольников. 39 Пример №1. 39 3.11.3 Формула средних прямоугольников. 40 Пример №1. 40 3.11.4 Формула трапеций. 41 Пример №1. 41 Заключение.. 42 Список литературы... 43
Теоретическое описание схемы Горнера Схема Горнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида
Пусть задан многочлен:
Пусть требуется вычислить значение данного многочлена при фиксированном значении
Определим следующую последовательность:
…
…
Искомое значение Р(x0)=b0 . Покажем, что это так. В полученную форму записи Р(x0) подставим х=x0 и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через
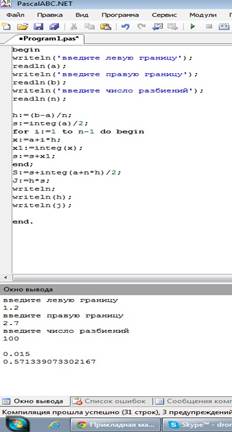
Begin {Вводим степень многочлена и значение х0} writeln('введите степень многочлена'); readln(n); writeln('введите аргумент'); readln(x0); {Цикл заполнения массива} For i:=1 to n+1 do begin writeln('введите коэффициент при степени ',n+1-i); readln(a[i]); b[i]:=a[i]; end; b[1]:=a[1]; {считаем значения b[i]} for i:=2 to n+1 do begin b[i]:=a[i]+b[i-1]*x0; end; {вывод ответов} For i:=1 to n+1 do begin writeln; writeln('степень: ',n+1-i); writeln('коэффициент при степени ',n+1-i,' = ',a[i]); writeln('элемент последовательности = ',b[i]); end;
{вывод итогового ответа} writeln; writeln('Ответ = ',b[n+1]); end. 1.4 Описание контрольного примера Найти значение многочлена по схеме Горнера в заданной точке х=х0:
Ответ: 1.5 Скриншот решения контрольного примера
1.6 Описание примера №2 Найти значение выражения по схеме Горнера:
при заданном многочлене:
1.7 Скриншот примера №2
Вычислительный практикум Вариант 14 Пример №1 Отделить изолированные корни следующего уравнения с помощью компьютерной программы:
Найдем ООФ: подкоренное выражение должно быть строго больше нуля 0.
Отсюда ООФ: любые числа строго большие -1.75. Примем интервал [-1.75;150]; подставим значения в программу:
Рис. 1. Скриншот решения примера №1
Ответ: на интервале [-1.75;150] содержится 2 корней, на интервалах:
Пример №2 Отделить изолированные корни следующего уравнения с помощью компьютерной программы на интервале [-10;10]: Подставим имеющиеся данные в программу:
Рис. 3. Скриншот решения примера №2
Ответ: на интервале [-10;10] содержится 8 корней, на интервалах:
Пример №1 Решить следующее уравнение методом дихотомии:
Рис. 1. Графики функций -0,5x и х2-3
Исходя из графиков, интервалы будут: [-2;0] и [0;2]. Подставим данные в программу:
Рис. 2. Скриншоты решения примера №1 Ответ: уравнение имеет 2 корня на интервалах:
Пример №2 Решить следующее уравнение методом дихотомии:
Рис. 3 Графики функций x2 и 1/2x Интервалы с корнями будут: [-3;-1] и [0;2]. Подставим полученные данные в программу:
Рис. 4. Скриншот решения примера №2 Ответ: уравнение имеет 2 корня на интервалах:
Пример №1 Для уравнения Производная равна: Решим квадратное уравнение:
Корни уравнения: x1=0; x2= -0.5; x3= 0.5;
Сузим интервалы:
Интервалы будут следующими: [-2;-0,5] и [0,5;2]. Подставим данные в программу:
Рис. 1. Скриншоты решения примера №1 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Пример №2 Для уравнения Производная равна: Решим квадратное уравнение:
Корни этого квадратного уравнения: x1=0; x2= -4; x3= 1.
Сузим интервалы:
Интервалы будут следующими: [-6;-4] и [1,4]. Подставим данные в программу:
Рис. 2. Скриншоты решения примера №2 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Пример №1 Решить уравнение объединенным методом
Рис. 1. Графики функций 0.5x-3 = (х+2)2 Интервал для нахождения корней: [-2;1]. Подставим полученные значения в программу:
Рис. 2. Скриншот решения примера №1 Ответ: на интервале [-2;1] уравнение имеет корень х1 = -1.644 Пример №2 Решить уравнение объединенным методом
Рис. 3 Графики функций x2– 3 и -0.5x Выделим 2 интервала, содержащих корни: [-2;0] и [0;2]. Подставим полученные значения в программу:
Рис. 4. Скриншот решения примера №2 Ответ: на интервале [-2;0] уравнение имеет корень х1 = -0.999; интервале [0;2] уравнение имеет корень х2 = 1.637
Пример №1 Для уравнения Производная равна: Решим квадратное уравнение:
Корни этого квадратного уравнения: x1=0; x2= -4; x3= 1.
Сузим интервалы:
Интервалы будут следующими: [-6;-4] и [1,4]. Подставим данные в программу:
Рис. 1. Скриншоты решения примера №1 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Пример №2 Для уравнения Производная равна: Решим квадратное уравнение:
Корни уравнения: x1=0; x2= -0.5; x3= 0.5;
Сузим интервалы:
Интервалы будут следующими: [-2;-0,5] и [0,5;2]. Подставим данные в программу:
Рис. 2. Скриншоты решения примера №2 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Пример №1 Решить следующее уравнение методом простых итераций:
Построим графики функций и отделим интервалы с корнями:
Рис. 1. Графики функций (х-1)2 и ех/2 Как видно из графиков, интервал, содержащий корень, только один: [0;2]. Подставим полученные данные в программу:
Рис. 2. Скриншот решения примера №1 Ответ: на интервале [0;2] уравнение имеет корень х = 0.231; Пример №2 Решить следующее уравнение методом простых итераций (при х>0):
Построим графики функций и отделим интервалы с корнями:
Рис. 3. Графики функций sin(0.5x)+1 и x2 Как видно из графиков, 2 интервала, содержащих корень: [-1;-0.5] и [1;1.5]. По условию необходимо взять х>0 => берем интервал [1;1.5]. Подставим значения в программу:
Рис. 4. Скриншот решения примера №2 Ответ: на интервале [1;1.5] корень уравнения х = 1.260 Пример №1 Решить систему линейных уравнений методом Гаусса:
Подставим коэффициенты при неизвестных и свободные члены в программу:
Рис. 1. Скриншот решения примера №1 Ответ: невязки уравнений близки по значению к 0, корни данной СЛУ равны:
Пример №1 Найти для заданной матрицы обратную методом Гаусса:
Подставим элементы матрицы в программу:
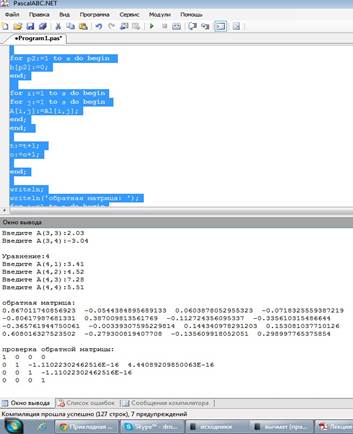
Рис. 1. Скриншот решения примера №1 Ответ: для заданной матрицы получена обратная, проверка перемножением дала единичную матрицу. Полученная обратная матрица:
Пример №2 Найти для заданной матрицы обратную методом Гаусса:
Подставим элементы матрицы в программу:
Рис. 2. Скриншот решения примера №2 Ответ: для заданной матрицы получена обратная, проверка перемножением дала единичную матрицу. Полученная обратная матрица:
Пример №1 Решить систему линейных уравнений методом простых итераций:
Подставим коэффициенты в программу:
Рис. 1. Скриншот решения примера №1 Ответ: решения данной СЛУ найдены на 27 шаге итерации, полученные значения корней равны:
Пример №2 Решить систему линейных уравнений методом простых итераций:
Подставим коэффициенты в программу:
Рис. 2. Скриншот решения примера №2 Ответ: решения данной СЛУ найдены на 27 шаге итерации, полученные значения корней равны:
Интерполирование функций Пример №1 Построить интерполяционный полином Лагранжа и вычислить с помощью него приближенное значение функции:
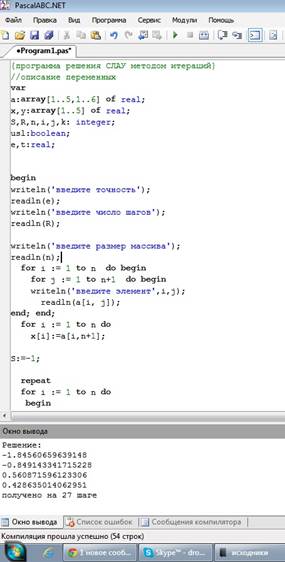
Вычислите значение функции у(х), при х = 0,445; 0,639; 0,702. Подставим данные в программу:
Рис. 1. Скриншоты решений примера №1 Ответ: y(0.445) = 1.664; y(0.639) = 2.078; y(0.702) = 2.234 Численное интегрирование Пример №1 Численно проинтегрировать выражение при помощи формулы левых прямоугольников:
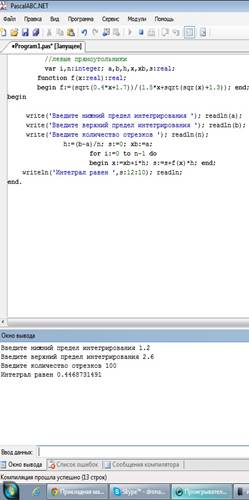
Рис. 1. Скриншот решения примера №1 Ответ: значение данного интеграла численно равно 0.447
Пример №1 Численно проинтегрировать выражение при помощи формулы правых прямоугольников:
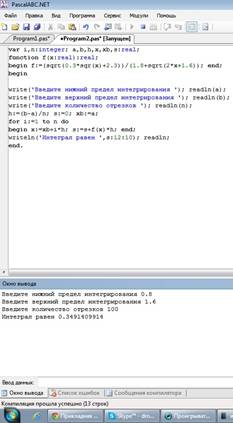
Рис. 1. Скриншот решения примера №1 Ответ: значение данного интеграла численно равно 0.349 Пример №1 Численно проинтегрировать выражение при помощи формулы средних прямоугольников:
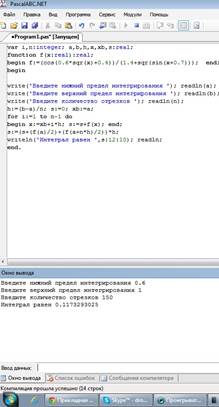
Рис. 1. Скриншот решения примера №1 Ответ: значение данного интеграла численно равно 0.117
Формула трапеций Пример №1 Численно проинтегрировать выражение при помощи формулы трапеций:
Рис. 1. Скриншот решения примера №1 Ответ: значение данного интеграла численно равно 0.571
Заключение Курсовая работа на тему «Нахождение значения многочлена по схеме Горнера»
Исполнитель Студент группы ЭМА-10 Каргаполов А.В. Руководитель Миронова Л.И.
Екатеринбург
Введение.. 4 1. Схема Горнера.. 5 1.1 Теоретическое описание схемы Горнера. 5 1.2 Пошаговый алгоритм нахождение значение многочлена по схеме Горнера. 7 1.3 Код программы, реализующей схему Горнера. 7 1.4 Описание контрольного примера. 8 1.5 Скриншот решения контрольного примера. 9 1.6 Описание примера №2. 10 1.7 Скриншот примера №2. 10 2. Презентационные материалы по методу «Схема Горнера». 11 3. Вычислительный практикум... 15 3.1 Отделение изолированных корней уравнения с помощью компьютерной программы 15 3.1.1 Пример №1. 15 3.1.2 Пример №2. 16 3.2 Уточнение корней с заданной точностью методом дихотомии. 17 3.2.1 Пример №1. 17 3.2.2 Пример №2. 18 3.3 Уточнение корней с заданной точностью методом хорд. 20 3.3.1 Пример №1. 20 3.3.2 Пример №2. 21 3.4 Уточнение корней с заданной точностью объединенным методом.. 23 3.4.1 Пример №1. 23 3.4.2 Пример №2. 24 3.5 Уточнение значения изолированного корня методом касательных. 26 3.5.1 Пример №1. 26 3.5.2 Пример №2. 27 3.6 Уточнение значения изолированного корня методом простых итераций. 29 3.6.1 Пример №1. 29 3.6.2 Пример №2. 30 3.7 Решение систем линейных уравнений методом Гаусса. 32 3.7.1 Пример №1. 32 3.8 Обращение матриц методом Гаусса. 33 3.8.1 Пример №1. 33 3.8.2 Пример №2. 34 3.9 Решение систем линейных уравнений методом простых итераций. 35 3.9.1 Пример №1. 35 3.9.2 Пример №2. 36 3.10 Интерполирование функций. 37 3.10.1 Пример №1. 37 3.11 Численное интегрирование. 38 3.11.1 Формула левых прямоугольников. 38 Пример №1. 38 3.11.2 Формула правых прямоугольников. 39 Пример №1. 39 3.11.3 Формула средних прямоугольников. 40 Пример №1. 40 3.11.4 Формула трапеций. 41 Пример №1. 41 Заключение.. 42 Список литературы... 43
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.39.16 (0.159 с.) |
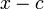 . Метод назван в честь Уильяма Джорджа Горнера.
. Метод назван в честь Уильяма Джорджа Горнера. .
.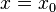 . Представим многочлен
. Представим многочлен  в следующем виде:
в следующем виде: .
.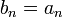



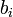 :
:



 ,
,





















 уточнить значение корня методом хорд.
уточнить значение корня методом хорд.




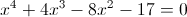 уточнить значение корня методом хорд.
уточнить значение корня методом хорд.