
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод деления отрезка пополам решения алгебраических уравнений.Стр 1 из 3Следующая ⇒
Метод деления отрезка пополам решения алгебраических уравнений. Другие названия: метод бисекции (bisectionmethod), метод дихотомии. Метод половинного деления – простейший численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [xL; xR], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие: f(xL) * f(xR) < 0. С непрерывности функции f(x) следует, что на интервале [xL; xR] существует, по крайней мере, один корень уравнения (если их несколько, то метод находит один из них). Выберем точку – середину интервала: xM = (xR + xL) / 2. Если f(xM) = 0, то корень найден. Если f(x)≠0, то разобьем этот интервал на два: [xL; xM] и [xM; xR]. Теперь найдем новый интервал, на котором функция изменяет знак. Повторим описанную процедуру до тех пор, пока не получим требуемую точность или превысим максимально допустимое количество итераций. Геометрическая интерпретация метода:
{ if (Helpers.Function(expression, Left) * Helpers.Function(expression, Right) >= 0) { throw new ArgumentException("F(a) and f(b) should have opposite signs."); }
intiterationCount = 0; double c;
do { c = (Left + Right) / 2; if (Helpers.Function(expression, Left) * Helpers.Function(expression, c) < 0) { Right = c; } else { Left = c; }
if (Math.Abs(Helpers.Function(expression, c)) <= epsilon || (Right - Left) <= epsilon || iterationCount == 1000) { break; }
iterationCount++; } while (true); return c; }
Метод простой итерации решения алгебраических уравнений. Уравнение f(x)=0 с помощью некоторых преобразований необходимо переписать в виде x=f(x). Уравнение f(x)=0 эквивалентно уравнению x=x+λ(x)f(x) для любой функции λ(x)≠0. Возьмем f(x)=x-λ(x)f(x) и выберем функцию (или переменную) λ(x)≠0 так, чтобы функция φ(x) удовлетворяла необходимым условиям. Для нахождения корня уравнения x=φ(x) выберем некоторое начальное значение x0, которое должно находиться как можно ближе к корню уравнения. Дальше с помощью итерационной формулы xn+1=φ(xn) будем находить каждое следующее приближение корня уравнения. Пример: x2-5x+6=0 Преобразования в вид x=f(x): x2-5x=-6, x*(x-5)=-6, x=-6/(x-5)=f(x). Реализация метода на C#: public static double SimpleIterations(string expression, double xa, double epsilon = 0.00001){double x = 0.0;doublexPrev = xa; variter = 0;do { x = Helpers.Function(expression, xPrev); if (Math.Abs(x - xPrev) <= epsilon || iter == 1000){break; }xPrev = x;iter++; }while (true);return x;}
4.Метод наименьших квадратов аппроксимации функций. Аппроксимация - приближенное выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов. При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости. Поэтому важно считывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. Численное решение обыкновенных дифференциальных уравнений. Метод Коши Численное решение уравнения Пуассона ПУАССОНА УРАВНЕНИЕ
численные методы решения - методы, заменяющие исходную краевую задачу для уравнения Пуассона ∆u (x) ≡ системой из Nлинейных алгебраич. решение к-рой В зависимости от способа сравнения решений исходной задачи (1) и дискретной задачи (2) определяются такие важнейшие понятия, как погрешность численного метода и оценка погрешности (точности). Другими характеристиками численных методов служат алгебраич. свойства систем (2) (дискретных аналогов краевых задач), связанные с устойчивостью их решений (корректностью дискретных задач) и возможностью отыскания точных или приближенных решений (2) теми или иными прямыми или итерационными методами при выполнении соответствующей вычислительной работы и соответствующих требованиях на объем используемой памяти ЭВМ (см. Минимизация вычислительной работы).
Важность численного решения краевых задач для П. у. определяется не только тем, что эти задачи часто возникают в разнообразных областях науки и техники, но и тем, что они нередко служат и средством решения более общих краевых задач как для уравнений и систем уравнений эллиптич. типа, так и различных нестационарных систем. Основными численными методами для решения рассматриваемых краевых задач являются проекционные методы и разностные методы.
12. Численное решение обыкновенных дифференциальных уравнений. Метод последовательных приближений Пикара. Этот метод позволяет получить решение дифференциального уравнения (1) в виде функции, представленной аналитически. Пусть в условиях теоремы существования требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части Очевидно, решение интегрального уравнения (5) будет удовлетворять дифференциальному уравнению (1) и начальному условию (2).
Действительно, при x=x0получим:. вместе с тем интегральное уравнение (5) позволяет применить метод последовательных приближений. Положим y=y0 и получим из (5) первое
приближение:. Интеграл в правой части содержит только переменную х; после нахождения этого интеграла будет получено аналитическое выражение приближения y1(x) как функции переменной х. Заменим теперь в уравнении (5) у найденным значением y1(x) и получим второе
приближение: и т.д. В общем случае итерационная формула имеет вид:
Циклическое применение формулы (6) дает последовательность функций
Так как функция f непрерывна в области G, то она ограниченна в некоторой области G??? G, содержащей точку (x0,y0), то есть
Применяя к уравнению (6) в условиях теоремы существования принцип сжимающих отображений, нетрудно показать, что последовательность (7) сходится. Ее предел является решением интегрального уравнения (1) с начальными условиями (2). Это озночает, что k- ый член последовательности (7) является приближением к точному решению уравнения (1) с определенной степенью точности. Оценка погрешности k -го приближения дается формулой:
Где М - константа Липшица (4), N - верхняя грань модуля функции f из неравенства (8), а величина d для определения окрестности
Сеток метод собирательное название группы приближённых методов решения дифференциальных, интегральных и интегро-дифференциальных уравнений. Применительно к дифференциальным уравнениям с частными производными термин «С. м.» используется в качестве синонима терминов «метод конечных разностей» и «разностный метод». С, м. — один из наиболее распространённых приближённых методов решения задач, связанных с дифференциальными уравнениями. Широкое применение С. м. объясняется его большой универсальностью и сравнительной простотой реализации на ЭВМ. Суть С. м. состоит в следующем: область непрерывного изменения аргументов, в которой ищется решение уравнения, дополненного, если необходимо, краевыми и начальными условиями, заменяется дискретным множеством точек (узлов), называемым сеткой; вместо функций непрерывного аргумента рассматриваются функции дискретного аргумента, определяемые в узлах сетки и называемые сеточными функциями; производные, входящие в уравнение, краевые и начальные условия, аппроксимируются разностными отношениями; интегралы аппроксимируются квадратурными формулами; при этом исходное уравнение (задача) заменяется системой (линейных, если исходная задача была линейной) алгебраических уравнений (системой сеточных уравнений, а применительно к дифференциальным уравнениям — разностной схемой).
Если полученная таким образом система сеточных уравнений разрешима, по крайней мере, на достаточно мелкой сетке, т. е. сетке с густым расположением узлов, и её решение при неограниченном измельчании сетки приближается (сходится) к решению исходного уравнения (задачи), то полученное на любой фиксированной сетке решение и принимается за приближённое решение исходного уравнения (задачи).
Метод деления отрезка пополам решения алгебраических уравнений. Другие названия: метод бисекции (bisectionmethod), метод дихотомии. Метод половинного деления – простейший численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [xL; xR], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие: f(xL) * f(xR) < 0. С непрерывности функции f(x) следует, что на интервале [xL; xR] существует, по крайней мере, один корень уравнения (если их несколько, то метод находит один из них). Выберем точку – середину интервала: xM = (xR + xL) / 2. Если f(xM) = 0, то корень найден. Если f(x)≠0, то разобьем этот интервал на два: [xL; xM] и [xM; xR]. Теперь найдем новый интервал, на котором функция изменяет знак. Повторим описанную процедуру до тех пор, пока не получим требуемую точность или превысим максимально допустимое количество итераций. Геометрическая интерпретация метода:
{ if (Helpers.Function(expression, Left) * Helpers.Function(expression, Right) >= 0) { throw new ArgumentException("F(a) and f(b) should have opposite signs."); }
intiterationCount = 0; double c;
do { c = (Left + Right) / 2; if (Helpers.Function(expression, Left) * Helpers.Function(expression, c) < 0) { Right = c; } else { Left = c; }
if (Math.Abs(Helpers.Function(expression, c)) <= epsilon || (Right - Left) <= epsilon || iterationCount == 1000) { break; }
iterationCount++; } while (true); return c; }
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.029 с.) |

 (1)
(1)
 ≡(
≡( ,
,  позволяет построить нек-рую аппроксимацию Pn Un для решения исходной задачи,N→∞.
позволяет построить нек-рую аппроксимацию Pn Un для решения исходной задачи,N→∞. уравнения (1) от x0 до х:
уравнения (1) от x0 до х:  ,
,
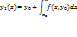

 (6).
(6). (7).
(7). (8).
(8).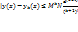 , (9)
, (9) вычисляется по формуле
вычисляется по формуле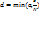 (10)
(10) 


