
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Код із кількістю одиниць у комбінації, кратною трьом⇐ ПредыдущаяСтр 12 из 12
Цей код можна утворити або додаванням до кожної комбінації початкового коду r = 2 перевірних елементів, або зменшенням кількості дозволених комбінацій початкового коду з накладанням додаткової умови: кількість одиниць у кожній комбінації має бути кратною трьом. У першому випадку до початкової кодової комбінації додаються два перевірних розряди, які мають такі значення, що сума одиниць у кодовій комбінації стає кратною трьом. Так, якщо початкова кодова комбінація має дві або п'ять одиниць, то для здобуття ваги w = 3 або 6 кодової комбінації треба доповнити її двома перевірними елементами 10. Якщо ж у початковій комбінації є одна або чотири одиниці, то вона доповнюється двома перевірними елементами 11. Так, комбінація 01010 початкового коду, закодована кодом із кількістю одиниць, кратною трьом, матиме вигляд 0101010, а 10000 → 1000011, 0110 → n011010, 101100 → 10110000, 110110 → 11011011, 0111011 → 011101110 тощо. У другому випадку з усіх комбінацій початкового коду вибирають тільки ті, які мають вагу w = 3 та 6. Решту комбінацій використовувати не можна. Код дає змогу виявити всі поодинокі помилки та деякі помилки більшої кратності, що призводять до порушення умови w = 3 або 6, де w - кількість одиниць у кодовій комбінації. Здатність коду виявляти помилкові комбінації майже така сама, як і коду зі сталою вагою. Надмірність коду з доповненням до необхідної кількості одиниць визначається виразом
а коду, що утворюється відбором із загальної кількості комбінацій з відповідною кількістю одиниць (3 або 6), - виразом
Коди, що виправляють помилки Коди, що виправляють помилки (або коректувальні коди) повинні мати мінімальну кодову відстань dmin ≥ 3. Її зростання досягається збільшенням кількості n розрядів коду або зменшенням кількості N д дозволених кодових комбінацій, які використовуються для передачі повідомлень, тобто підвищенням надмірності коду. Найбільшого поширення серед двійкових коректувальних кодів дістали систематичні та несистематичні блокові коди (вони, у свою чергу, поділяються на лінійні та нелінійні), а також рекурентні коди. З недвійкових кодів для захисту інформації від помилок застосовуються узагальнений код Хеммінга, ланцюговий та ітеративний коди.
Двійкові групові коди 8.1.1 Лінійний систематичний груповий (блоковий код) Застосувавши теорію лінійних просторів, можна дати таке визначення: лінійним систематичним груповим двійковим (n, k)- кодом називається код, у якого перевірні елементи bj (де j = 1... r) знаходяться як суми за модулем 2 обумовлених інформаційних елементів аі (де i = 1... k). У нелінійних двійкових (n, k)-кодах перевірні елементи знаходяться інакше. Таким чином, у лінійному коді перевірні елементи визначаються як
де ∑O - знак суми за модулем 2; αji - коефіцієнти, значення яких дорівнюють 0 або 1. Як випливає з (8.1), закон побудови лінійного коду визначається вибором kr коефіцієнтів αji. Одна з властивостей лінійних кодів полягає в тому, що сума за модулем 2 будь-яких двох дозволених кодових комбінацій також є дозволеною комбінацією цього коду. Нехай є дві дозволені кодові комбінації лінійного коду
перевірні символи яких визначаються відповідно виразами
При додаванні за модулем 2 комбінацій V (1) і V (2) дістанемо комбінацію V (3), яка також буде комбінацією цього коду:
де
тому що при додаванні за модулем 2 діють асоціативний, комутативний та дистрибутивний закони. Таким чином,
де
Така властивість дає можливість побудувати всі дозволені комбінації лінійного коду, маючи тільки обмежену кількість їх. При цьому побудова лінійного коду виконується на основі твірної (погоджувальної) матриці. Ця матриця будується так, щоб: 1) кількість початкових кодових комбінацій дорівнювала k, тобто кількості інформаційних елементів первинного коду; 2) всі початкові кодові комбінації були різними; 3) нульова комбінація не входила до складу початкових; 4) всі початкові комбінації були лінійно незалежними; 5) кількість одиниць в кожній початковій комбінації була не меншою ніж dmin;
Підібрані за цим правилом початкові комбінації записуються у вигляді твірної матриці G(n, k),яка містить k рядків і n стовпців:
Матрицю (8.2) можна подати також у вигляді двох підматриць: інформаційної Еk та перевірної С (r, k). Першу зручно записати в канонічній формі як одиничну підматрицю, що має k стовпців і стільки ж рядків:
Перевірна підматриця С (r, k) будується підбором r -розрядних комбінацій з кількістю одиниць в рядку не меншою від (dтіп - 1). При цьому необхідно враховувати, що сума за модулем 2 будь-яких розрядів повинна мати більш як (dтіп - 2) одиниць. Ураховуючи викладене, в межах теорії матриць можна дати таке визначення: лінійним систематичним груповим двійковим (n, k)- кодом називається код, у якого всі його (2 k - 1) ненульові комбінації можуть бути утворені як суми за модулем 2 рядків деякої матриці G (n, k), розміром k Розглянемо приклад побудови матриці систематичного групового коду, здатного виправляти однократну помилку (v вп = 1) при передачі 16 повідомлень (N д =16). Відомо, що N д = 2k, звідки k = 4 (N д= 16 = 24). Отже, кількість рядків твірної матриці G (n, k) дорівнює 4, а кількість стовпців - довжині п коду (n = k + r, де r = 3 для v вп = 1 і dтіп = 2 v вп + 1 = 3), тобто кількість стовпців підматриці G (r, k )становить 3. Кількість перевірних розрядів можна визначити, користуючись табл. 8.1.
Таблиця 8.1 – Визначення перевірних розрядів
Згідно з правилом побудови підматриці C (r, k )кількість одиниць в ній має бути не меншою ніж dтіп – 1 = 3 - 1 = 2. З триелементних комбінацій для підматриці C (r, k )вибираємо тільки ті, в яких кількість одиниць більша двох: 110, 101, 011, 111. Через те, що як інформаційна Еk використовується одинична підматриця, твірна матриця лінійного коду для розглядуваного прикладу, тобто коду, який виправляє одну помилку, остаточно має вигляд
Рядки в перевірній підматриці C (r, k )можна міняти місцями. При цьому дістанемо кілька варіантів твірних матриць для прикладу, що розглядається. Побудуємо за допомогою поданої раніше твірної матриці всі комбінації розглядуваного (7,4)-коду. Оскільки перша комбінація - нульова, друга - п'ята комбінації є рядками твірної матриці, решту 11 знайдемо підсумовуванням за модулем 2 всіх можливих комбінацій рядків твірної матриці. Всі 16 комбінацій (7, 4)-коду з цією матрицею матимуть такий вигляд: 1. 0000000; 9. 0110011 (3 2. 1000011; 10. 0101010 (3 3. 0100101; 11. 0011001 (4 4. 0010110; 12. 1110000 (2 5. 0001111; 13. 0111100 (3 6. 1100110 (2 7. 1010101 (2 8. 1001100 (2 При побудові комбінацій лінійного коду за твірною матрицею необхідно вміти знаходити перевірні розряди кодових комбінацій за інформаційними. Алгоритм утворення перевірних розрядів за допомогою твірної матриці G (n, k )за відомим інформаційним має вигляд
Система перевірок для кожної конкретної матриці G (n, k) формулюється так: у першу перевірку разом із перевірним розрядом b 1входять інформаційні розряди, що відповідають одиницям першого стовпця підматриці C (r, k );у другу - перевірний розряд b 2та інформаційні розряди, які відповідають одиницям другого стовпця під матриці C (r, k ) і т. д. Кількість перевірок дорівнює кількості перевірних розрядів коду, тобто кількості стовпців під матриці C (r, k ). Система перевірок для наведеної вище твірної матриці G (7, 4) має вигляд Опираючись на твірну матрицю, можна побудувати перевірну матрицю Н,яка містить r рядків, п стовпців і складається з двох підматриць: D (k, r ), що має k стовпців і r рядків, кожний рядок якої відповідає транспонованому стовпцю перевірних розрядів підматриці C (r, k ) твірної матриці G (n, k ); одиничної підматриці Еr:
Ця перевірна матриця дає змогу спростити операції кодування та декодування. Позиції, зайняті одиницями в i -му рядку підматриці D (k, r ),визначають ті інформаційні розряди, які мають брати участь у формуванні i -го перевірного розряду. Кількість розрядів кодового синдрому і, як наслідок, кількість перевірних елементів при виправленні однократних помилок визначається нерівністю 2 r - 1 ≥ п або 2 r - 1 ≥ С 1 п. Для виправлення не тільки однократних, а й помилок більшої кратності необхідно виконати умову
де v вп - кратність виправленої помилки. Як приклад перетворимо твірну матрицю (8.3) на перевірну
Перевірними елементами, що визначаються за допомогою матриці, будуть Методи виправлення помилок у систематичному груповому коді. Розрізняють два основних таких методи: за допомогою кодового синдрому та за допомогою кодів-супутників. Використання кодового синдрому. Перевірка кодової комбінації, що приймається, при цьому виконується зіставленням її перевірних розрядів з перевірними розрядами, які обчислюються на основі прийнятих інформаційних. Кодові комбінації, що передаються та приймаються, запишемо відповідно у вигляді
З метою виявлення помилки в кодовій комбінації, що приймається, зробимо перевірки
та порівняємо ці значення зі значеннями прийнятих перевірних елементів
Після підстановки (8.6) у (8.7) знайдемо значення кожного елемента Sj. в наборі (8.7):
Набір елементів (S 1,..., Sr) називається синдромом (пізнавачем) помилок. За відсутності помилки комбінація синдрому складається з одних нулів. Присутність хоча б одного ненульового елемента в комбінації синдрому вказує на спотворення елемента у прийнятій кодовій комбінації. Між комбінацією синдрому та помилковою комбінацією, що і причинила створення синдрому, немає взаємної однозначної відповідності, тому за кожним синдромом закріплюється така комбінація помилок, що виправляється, виникнення якої в каналі є найімовірнішим.
Значення синдрому збігаються з комбінацією результатів перевірки на парність, які визначаються перевірною матрицею Н. Так, синдром для систематичного (7,4)-коду з перевірною матрицею (8.5) визначається виразами Якщо значення
Установимо відповідність виду синдрому з видом помилки, що виправляється, для перевірної матриці Н (табл. 8.2). Таблиця 8.2 – Відповідність виду синдрому з видом помилки
Якщо при передачі по каналах у кодовій комбінації виникне одноразова помилка в одному з розрядів, то обчислений на приймальному боці синдром укаже номер спотвореного розряду. Побудова синдромів для виправлення подвійних, потрійних і помилок більшої кратності складна. Тому метод виправлення помилок за допомогою кодового синдрому використовується головним чином для виправлення поодиноких помилок, імовірність виникнення яких значно більша, ніж помилок більшої кратності. Розглянутий вище лінійний систематичний груповий код належить до досконалих кодів. Досконалим лінійним кодом називається такий оптимальний за dтіп лінійний код, у якого кількість ненульових комбінацій синдрому (2 r - 1)дорівнює кількості всіх можливих комбінацій помилок із вагою v впй менше, а кожна з (2 r - 1)груп із 2 k комбінаціями помилок, які утворюють ненульові комбінації синдрому, має тільки одну із зазначених комбінацій помилок. Так, лінійний (7,4)-код, який задається перевірною матрицею (8,5), є досконалим лінійним кодом, тому що при dтіп = 3 та здатності виправлення поодиноких помилок кількість ненульових комбінацій синдрому (23 - 1 = 7) дорівнює кількості всіх можливих комбінацій однократних помилок (див. табл. 8.2). Використання кодів-супутників. Цей метод передбачає побудову кодової таблиці з кодами-супутниками за таким правилом (табл. 8.3): в першому її рядку розташовують усі кодові комбінації Vі, для яких необхідно знайти коди-супутники; в другому рядку записують вектори, утворені підсумовуванням за модулем 2 кодових комбінацій Vі з вектором помилки е 1, вага якого w = 1, а одиниця знаходиться в першому розряді; третій рядок є результатом підсумовування за модулем 2 кодових комбінацій Vі з вектором e 2,вага якого w = 1, а одиниця розміщується в другому розряді, і т. д. Так діють доти, доки не будуть підсумовані з кодовими комбінаціями Vі всі вектори еі вагою w = 1 з одиницями в кожному з п розрядів, потім підсумовують за модулем 2 вектори еі вагою w = 2 з послідовним перекриванням усіх можливих розрядів (вага векторів еі визначає кількість помилок, що виправляються, а розрядність цих векторів відповідає розрядності кодової комбінації).
Таким чином, для кожної кодової комбінації Vі лінійного систематичного коду дістають свою групу кодів-супутників, розташованих у відповідному стовпці (див. табл. 8.3), які зберігаються в пам'яті ЕОМ. У разі приймання комбінації, що збігається з одним із кодів-супутників, спотворена комбінація розшифровується як початкова робоча комбінація, до якої належить цей код-супутник.
Таблиця 8.3 – Відповідність кодової комбінації систематичного коду групі кодів-супутників
Недоліками розглянутого методу є велика ємність пам'яті ЕОМ і значні затрати часу на перебір комбінацій кодів-супутників. Укорочені лінійні систематичні коди. Розрізняють повні та вкорочені лінійні систематичні коди. До перших належать лінійні (n, k)-коди, що містять 2 k комбінацій, а до других - лінійні (п, k, i)-коди (де і = 1... k - 1), які мають 2 k -1комбінацій. Укорочений лінійний систематичний код утворюють з повного коду, при цьому дістають кодову відстань dтіп, не меншу ніж у початкового лінійного систематичного коду зі збереженням такої самої кількості перевірних елементів, тобто r = (n - і) - (k - і) = n - k. Здобуття вкороченого лінійного систематичного коду ґрунтується на тому, що оскільки з загальної кількості 2 k комбінацій первинного коду, які потрібно закодувати лінійним систематичним кодом, 2 k -1 комбінацій починаються з 0, а 2 k -1 - з 1, після кодування лінійного (n, k)-коду 2 k -1 його комбінацій також починатимуться з 0. Ці 2 k -1 комбінацій розглядатимемо як новий лінійний систематичний код. Тоді, через те що вони належать початковому (n, k)-коду, кодова відстань dтіп нового коду буде не меншою, ніж початкового. Нульовий символ на початку кодової комбінації зберігається й після кодування її лінійним (n, k)-кодом, причому в утворенні перевірних елементів лінійного систематичного коду участі він не бере. З урахуванням цього нульовий символ можна відкинути. При цьому дістанемо лінійний (n -1, k - 1)-код, тобто код, що містить п - 1 елементів, з яких k - 1 є інформаційними, а r - перевірними. Укорочений лінійний систематичний код легко дістати з повного лінійного (n, k)-коду, що подається у вигляді твірної матриці G (n, k ) розміром k Так, твірну й перевірну матриці вкороченого лінійного систематичного (6, 3)-коду можна дістати з відповідних матриць G (7, 4) (8.3) та H (7, 3) (8.5) повного коду:
Після вкорочення на один символ лінійного систематичного (n -1, k - 1)- коду здобудемо вкорочений (n -2, k - 1)- код і т. д. Коди Хеммінга Це одні з найпоширеніших систематичних кодів, які виправляють помилки. До кодів Хеммінга належать коди з мінімальною кодовою відстанню dтіп = 3, що виправляють всі поодинокі помилки. Формування r перевірних елементів у комбінаціях цих кодів виконують за k інформаційними елементами. Таким чином, довжина кодової комбінації n = k + r. Перевірними елементами є лінійні комбінації інформаційних елементів, тобто зважені суми інформаційних елементів з ваговими коефіцієнтами 1 та 0. Послідовність одиниць і нулів у кодовій комбінації називається ще кодовим вектором. Кодам Хеммінга притаманні властивості лінійних кодів: сума (різниця) векторів лінійного коду дає вектор, який належить цьому коду; лінійні коди утворюють алгебричну групу відносно операції додавання за модулем 2; мінімальна кодова відстань між векторами групового коду дорівнює мінімальній вазі ненульових кодових векторів. При передачі кодового вектора може бути спотворений будь-який елемент, кількість таких ситуацій 2 r ≥ n + 1. (8.10) Оскільки 2 n = 2 k+r = 2 k · 2 r, можна записати 2 n ≥ (n + 1) · 2 k, (8.11) де 2 n - повна кількість комбінацій коду. Мінімальне співвідношення коректувальних та інформаційних розрядів, нижче якого код не може зберігати задані коректувальні властивості, визначається виразом 2 n - 1 = n. Для розрахунку основних параметрів кодів Хеммінга можна задати кількість перевірних елементів r; тоді з останнього виразу визначається n, а кількість інформаційних елементів k = n - r. Співвідношення між r, n, k для кодів Хеммінга наведемо в табл. 8.4. Таблиця 8.4 – Співвідношення r, n, k для кодів Хеммінга
Характерна особливість перевірної матриці коду з dтіп = 3 полягає у тому, що її стовпці є різними ненульовими комбінаціями завдовжки r. Наприклад, при r = 4, п = 15 перевірна матриця (15, 11)-коду може мати такий вигляд:
Таким чином, якщо взяти комбінації чотириелементного двійкового простого коду й відкинути ненульову комбінацію, можна досить легко дістати перевірну матрицю, записавши всі кодові комбінації послідовно в стовпці матриці Н. Після переставлення стовпців, які мають одну одиницю, матриця (8.12) набуває вигляду
Згідно з матрицею (8.13) дістаємо систему перевірних рівнянь, за допомогою яких знаходимо перевірні розряди:
Поява помилки в кодовій комбінації веде до невиконання тих перевірних співвідношень (8.14), в які входить значення помилкового розряду. Так, якщо помилка виникла в сьомому інформаційному розряді (спотвореним є елемент а 7), то не виконуються перше, третє та четверте співвідношення (8.14), тобто синдром дорівнює 1011 [збігається з сьомим стовпцем матриці Н (8.13)]. Таким чином, місцезнаходження стовпця матриці Н, що збігається зі знайденим синдромом, визначає місце помилки. Обчислене значення синдрому обов'язково збігається з одним із стовпців матриці Н,тому що як стовпці вибираються всі можливі r -розрядні двійкові комбінації. Р. Хеммінг запропонував розташувати стовпці перевірної матриці так, щоб номер і -го стовпця матриці Н і номер розряду кодової комбінації відповідали двійковому поданню числа і. Тоді синдром, знайдений з перевірних рівнянь, буде двійковим поданням номера розряду кодової комбінації, в якій виникла помилка. Для цього перевірні розряди мають знаходитися не в кінці кодової комбінації, а на номерах позицій, які подаються степенем двійки (20, 21, 22, 23,...,2 r -1), як у матриці (8.12), тому що кожний з них входить тільки до одного з перевірних рівнянь. В останньому випадку перевірні розряди розміщуються між інформаційними. Синдром відповідно до перевірної матриці (8.12) визначається з системи рівнянь
Як перевірні вибираються розряди и 1, и 2, и 4та и 8 що зустрічаються в системі рівнянь (8.15) по одному разу. Наприклад, якщо необхідно закодувати повідомлення 11001010110 двійкового простого коду (k = 11) у коді Хеммінга, то потрібно визначити перевірні розряди в комбінації u 1 u 21 u 4100 u 81010110. З перевірної матриці (8.12) маємо
Обчислюючи и 1, и 2, и 4та и 8згідно з (8.16), дістаємо
Отже, комбінація коду Хеммінга для розглядуваного повідомлення матиме вигляд 111110001010110. Тепер припустимо, що шостий елемент цієї комбінації приймається помилково, тобто одержано повідомлення 111111001010110. Обчислюючи синдром за допомогою системи рівнянь (8.15), знаходимо S 1 = 0; S 2= 1; S 3 = 1; S 4 = 0, тобто синдром має вигляд 0110. Якщо це двійкове число перевести в десяткове, то дістанемо 6(0 · 23 + 1 ·22 + 1 · 21 + 0 · 20 = 6).Таким чином, необхідно виправити шостий розряд повідомлення, що надійшло.
Циклічні коди Ці коди також широко застосовуються для захисту інформації від помилок. Подання комбінацій в циклічних кодах виконують у вигляді поліномів формальної змінної x, що дає змогу звести дії над кодовими комбінаціями до дій над поліномами. Лінійні систематичні (n, k)-коди, в яких циклічний зсув an -2, an -3, an -4, …, a 2, a 1, a 0, an -1 дозволеної комбінації an -1, an -2, an -3, …, a 1, a 0 також є дозволеною комбінацією, що належить цьому коду, називаються циклічними. Така циклічна перестановка елементів виникає після множення полінома на х. Якщо V (x) = an -1 xn -1 + an -2 xn -2 + … + a 1 x + a 0, то xV (x) = an -1 xn + an -2 xn -1 +… … + + a 1 x 2 + a 0 x. Щоб степінь полінома не перевищував n – 1, член an -1 xn замінюється одиницею. Тому xV (x) = F (x) = an -2 xn -1 + … + a 1 x 2 + a 0 x + an -1. Особливу роль у теорії циклічних кодів відіграють твірні поліноми. Помічено, що комбінації лінійного коду мають властивість циклічності, коли як твірні використовуються поліномами, що є дільниками двочлена xn + 1. Кожний такий двочлен може бути розкладений на кілька незвідних поліномів, тобто таких, які можуть бути подані у вигляді добутку поліномів нижчих степенів (вони діляться самі на себе або на одиницю). Як твірні поліноми різних циклічних кодів можуть бути застосовані всі незвідні поліноми та добутки їх, тому що вони також є дільниками двочлена xn + 1. З урахуванням викладеного можна дати ще одне визначення двійкового циклічного коду: циклічним називається лінійний двійковий систематичний (n, k)-код, всі 2 k комбінацій якого подано поліномами степеня х – 1 і менше, що діляться на деякий поліном Р (х) степеня r = n – k, який є дільником двочлена xn + 1. Деякі твірні поліноми наведено в табл. 8.5.
Таблиця 8.5 – Твірні поліноми циклічних кодів
Розрізняють алгебричні та матричні методи побудови циклічного коду. Побудова дозволеної кодової комбінації (алгоритм кодування) перших зводиться ось до чого: - подати інформаційну частину з k елементів у вигляді полінома Q (x) степеня k -1; - помножити Q (x) на xr що еквівалентно зсуву k -розрядної кодової комбінації на r розрядів); - поділити поліном xr Q (x) на вибраний твірний поліном P (x), степінь якого дорівнює r, і визначити остачу від ділення R (x), тобто
де С (х) – частка від ділення, яка має той самий степінь, що й поліном Q (x); R (x) – остача від ділення, яка має степінь, не більший від r – 1 [менший, ніж степінь дільника P (x)]. Зазначимо, що r розрядів остачі є r перевіреними елементами кодової комбінації, причому
або
де F (x) – комбінація циклічного коду. З виразу (8.19) випливають два рівноцінних алгебричних методи побудови комбінацій циклічного коду:
Ще один метод можна дістати, замінивши в (8.21) частку від ділення С (х) на поліном Q (x) кодової комбінації r -елементного двійкового простого коду, що подається для кодування циклічним кодом. Ця заміна цілком слушна, оскільки поліноми С (х) і Q (x) мають однаковий найбільший степінь (однакову кількість розрядів). Отже,
У комбінаціях циклічних кодів, побудованих за першим і другим методами [див. вирази (8.20) і (8.21)], розташування інформаційних і перевірних елементів підпорядковується такому правилу: k старших розрядів комбінації є інформаційними, решта n – k = r розрядів – перевірними. При використанні третього методу побудови циклічних кодів [див. вираз (8.22)] дістають комбінації неподільного циклічного коду, в яких інформаційні та перевірні елементи не відокремлені один від одного, що ускладнює процес декодування. Тому на практиці найпоширенішими є перші два алгебричні методи побудови циклічного коду. Очевидно, що комбінація F (x) має ділитися на поліном P (x) без остачі. На цьому й ґрунтується перевірка комбінації на наявність помилок при її прийманні. Якщо прийнята комбінація F (x) ділиться на поліном P (x) без остачі, то вона визнається безпомилковою. Розрізняють два матричних методи побудови циклічного коду на основі твірної матриці G ц. Перший з них ґрунтується на вже відомому виразі (8.17). Відповідний рядок твірної матриці G ц записується у вигляді Для побудови твірної матриці (формування її рядків) беруть не довільні комбінації Q (x) двійкового простого коду, а тільки ті з них, які містять одиницю в одному розряді Qi (x), де i = 1, 2, …, k. Ці комбінації множать на xr і знаходять остачу від ділення Qi (x) xr / P (x), що дорівнює Ri (x). Так, для циклічного (7, 4)-коду з п = 7, k = 4 і твірним поліномом Р (х) = = х 3 + х 2 + 1, щоб побудувати твірну матрицю, вибирають чотириелементні одиничні комбінації Qi, двійкового простого коду: Q 1(х)= 1 (0001); Q 2(х) = х (0010); Q 3(x) = х 2(0100); Q 4(х) = x 3(1000). Вибрані комбінації Qi (х)множать на x 3 (r = п – k = 7 - 4 = 3),ділять на Р (х) = х 3 + х 2 + 1 і знаходять остачі:
Таким чином, твірна матриця для розглядуваного прикладу матиме вигляд
Твірна матриця має змогу дістати k комбінацій коду. Решту 2 k - k - 1 комбінацій, крім нульової, знаходять додаванням за модулем 2 рядків твірної матриці в усіх можливих сполученнях. Остання комбін
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.82.23 (0.135 с.) |


 (8.1)
(8.1)




 або
або 
 6) кодова відстань між будь-якими парами початкових комбінацій також була не меншою ніж dтіп.
6) кодова відстань між будь-якими парами початкових комбінацій також була не меншою ніж dтіп. (8.2)
(8.2)
 п, яка називається твірною матрицею коду.
п, яка називається твірною матрицею коду. (8.3)
(8.3) 4);
4);

 (8.4)
(8.4)
 (8.5)
(8.5)

 (8.6)
(8.6) . У результаті порівняння дістанемо r -елементний набір (S 1,..., Sr),що визначається як сума за модулем 2 двох r -елементних наборів:
. У результаті порівняння дістанемо r -елементний набір (S 1,..., Sr),що визначається як сума за модулем 2 двох r -елементних наборів: (8.7)
(8.7) (8.8)
(8.8) де перевірний елемент прийнятої кодової комбінації,
де перевірний елемент прийнятої кодової комбінації,  - і -йперевірний елемент, обчислений за інформаційними елементами на приймальному боці. Для (7,4)-коду маємо
- і -йперевірний елемент, обчислений за інформаційними елементами на приймальному боці. Для (7,4)-коду маємо 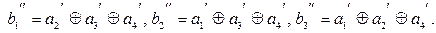
 підставити у вираз Si, то дістанемо
підставити у вираз Si, то дістанемо
 n виду (8.2) виключенням з матриці перших рядка та стовпця. В результаті дістанемо твірну матрицю G (n-1, k -1) нового вкороченого лінійного систематичного коду розміром (k - 1)
n виду (8.2) виключенням з матриці перших рядка та стовпця. В результаті дістанемо твірну матрицю G (n-1, k -1) нового вкороченого лінійного систематичного коду розміром (k - 1) 
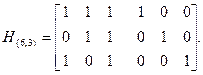 (8.9)
(8.9) . До цього слід додати ще одну ситуацію, коли помилка не виникає. Таким чином, загальна кількість 2 r комбінацій перевірних елементів має перевищувати кількість можливих помилкових ситуацій в коді з урахуванням відсутності помилок для правильного розрізнення їх і визначення місць помилки:
. До цього слід додати ще одну ситуацію, коли помилка не виникає. Таким чином, загальна кількість 2 r комбінацій перевірних елементів має перевищувати кількість можливих помилкових ситуацій в коді з урахуванням відсутності помилок для правильного розрізнення їх і визначення місць помилки: (8.12)
(8.12) (8.13)
(8.13) (8.14)
(8.14) (8.15)
(8.15)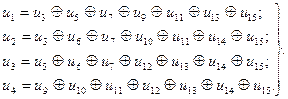 (8.16)
(8.16)
 (8.17)
(8.17)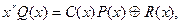 (8.18)
(8.18) (8.19)
(8.19)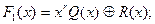 (8.20)
(8.20) (8.21)
(8.21) (8.22)
(8.22) При цьому вся матриця розбивається на дві під матриці, як і в лінійному систематичному груповому коді:
При цьому вся матриця розбивається на дві під матриці, як і в лінійному систематичному груповому коді:  , де
, де  - транспонована одинична інформаційна під матриця;
- транспонована одинична інформаційна під матриця;  - перевірна під матриця з кількістю стовпців r і рядків k, що утворюється остачами від ділення Ri (x). Такий метод дає можливість дістати твірну матрицю в канонічному вигляді.
- перевірна під матриця з кількістю стовпців r і рядків k, що утворюється остачами від ділення Ri (x). Такий метод дає можливість дістати твірну матрицю в канонічному вигляді.
 (8.23)
(8.23)


