
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное распределение (закон равномерного распределения – закон равномерной плотности).
Говорят, что СВ Х имеет равномерное распределение на участке от a до b, если ее плотность f(x) на этом участке постоянна Следовательно, каждое из значений х СВ Х равновероятно на участке (a,b), т.е. плотность вероятности на этом интервале постоянна, а вне его равна 0: Значение f(x) в крайних точках a и b участка (a,b) не учитываются, т.к. вероятность попадания в любую из этих точек для НСВ равна 0. Кривая равномерного распределения имеет вид прямоугольника, опирающегося на участок (a,b); в связи с этим равномерное распределение иногда называют «прямоугольным».
Рисунок 5.12 Найдем значение с. Следовательно,
Рисунок 5.13 Примеры равномерного распределения 1. Распределение ошибки квантования при представлении чисел Равномерное распределение имеют и ошибки, возникающие от округления данных при расчетах (в частности, на ЭВМ). Производится измерение какой-то величины с помощью прибора с грубыми делениями. В качестве приближенного значения измеряемой величины берется: a) ближайшее целое; b) ближайшее меньшее целое; c) ближайшее большее целое. Рассматривается СВ Х – ошибка измерения. Так как ни одно из значений СВ ничем не предпочтительнее других, естественно, что СВ Х распределена равномерно: в случае а) – на участке (-1/2; +1/2); в случае b) – на участке (0; 1) в случае c) – на участке (-1; 0) (в качестве 1 берется цена деления) 2. В современной вычислительной технике при моделировании случайных процессов часто используется СВ Х, имеющая равномерное распределение в пределах 0 до 1: Эта величина, которую коротко называют «случайным числом от 0 до 1», служит исходным материалом, из которого путем соответствующих преобразований получаются СВ с любым заданным распределением. Показательное распределение Говорят, что НСВ Х имеет показательное (или экспоненциальное) распределение, если Или, короче Положительная величина
Рисунок 5.14 График функции распределения имеет вид:
Рисунок 5.15
Показательное распределение играет большую роль в теории марковских случайных процессов, теории массового обслуживания и теории надежности. Дискретным аналогом экспоненциального распределения является геометрическое распределение.
Экспоненциально распределенная СВ Х обладает важным свойством: отсутствием последействия. Отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин. Экспоненциальное распределение тесно связано с распределением Пуассона, а именно: если времена между последовательными наступлениями некоторого события представляют собой независимые (определение независимости случайных величин будет дано позже) экспоненциально распределенные (с одним и тем же параметром Нормальное распределение Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов особое положение. СВ Х распределена по нормальному закону с параметрами Постоянная с определяется из условия нормировки f(x) (2-го свойства f(x)). Найдем Специальная функция, называемая функцией распределения Лапласа или «интегралом вероятностей», имеет вид: Для нее составлены таблицы значений и известно, что Следовательно, имеем Тогда, Смысл параметров будет установлен позже. Найдем функцию распределения F(x) для нормального закона распределения. Кривая нормального распределения имеет симметричный колоколообразный (холмообразный) вид. Она симметрична относительно прямой х=а и достигает максимума при х=а, имеет две точки перегиба при
Рисунок 5.16
Найдем вероятность попадания СВ Х в интервал Интеграл Замечание. Следует обратить внимание на пределы функции Иногда имеются таблицы значений не
Функции С помощью функции
Свойства функции Ф(х): 1) Ф(0) = 0; 2) Ф(-х) = - Ф(х) - нечетная функция; 3) Ф(+∞) = 0,5 (при х 4) Ф(-∞) = - 0,5
Свойства функции Ф*(х): 1) Ф*(0) = 0,5; 2) Ф*(-х) = 1 – Ф*(х) - нечетная функция; 3) Ф*(+∞) = 1; 4) Ф*(-∞) = 0.
Наиболее просто выражаются через функцию Лапласа вероятность попадания нормально распределенной СВ Х на участок длиной 2l, симметричный относительно центра рассеивания а.
Рисунок 5.18
При использовании Через функцию Лапласа выражается и функция распределения F( x) нормально распределенной СВ Х. По формуле (9), полагая Нормальное распределение возникает тогда, когда величина Х образуется в результате суммирования большого числа независимых (или слабозависимых) случайных слагаемых, сравнимых по своему влиянию на рассеивание суммы. Нормальное распределение имеет важное значение для практики. Распределение многих важных практических СВ оказывается подчиненным нормальному закону (рассеивание снарядов при стрельбе в цель и т.д.). Далее увидим, что «универсальность» этого закона объясняется тем, что СВ, равная сумме большого числа независимых СВ оказывается распределенной почти по нормальному закону. Кроме рассмотренных распределений непрерывных случайных величин существую и другие, важные для практики распределения: - Распределение Вейбулла, - Гамма-распределение, - Распределение Эрланга, - Распределение хи-квадрат. Считают, что распределению Вейбулла подчиняются времена безотказной работы многих технических устройств. При определенных значениях одного из параметров этого распределения оно превращается в экспоненциальное распределение или в распределение Релея. Гамма-распределение также достаточно хорошо описывает времена безотказной работы различных технических устройств. Распределение Вейбулла и гамма-распределение весьма близки между собой. Основным преимуществом закона Вейбулла перед гамма-распределением является то, что его функция распределения является элементарной функцией. Распределение Эрланга находит важные применения в теории массового обслуживания. Роль распределения хи-квадрат в математической статистике невозможно переоценить. Так, например, при проверке статистических гипотез о законе распределения используются критерии согласия. Существует несколько критериев согласия: - Критерий Хи-квадрат (критерий Пирсона), - Критерий Колмогорова, - Критерий Смирнова, - Др. Критерий Пирсона широко применяется для проверки гипотезы о нормальном распределении генеральной совокупности, применяется также и для других распределений. В этом состоит его достоинство.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.160.61 (0.017 с.) |
 .
.
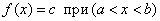 .
.

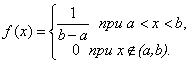 или
или 


 .
.
 .
. называется параметром показательного распределения. График показательного распределения имеет вид:
называется параметром показательного распределения. График показательного распределения имеет вид:

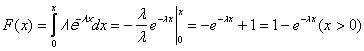 ,
, .
.
 , если ее плотность распределения имеет вид:
, если ее плотность распределения имеет вид: .
.
 ?
?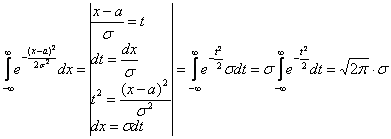 .
. - известный интеграл Эйлера-Пуассона.
- известный интеграл Эйлера-Пуассона. .
. .
.
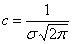 и
и  .
. .
. . При
. При  f(x) асимптотически приближается к оси Ох. При увеличении
f(x) асимптотически приближается к оси Ох. При увеличении  кривая становится более пологой.
кривая становится более пологой.

 .
.
 не выражается через элементарные функции, но его можно выразить через интеграл Лапласа.
не выражается через элементарные функции, но его можно выразить через интеграл Лапласа. .
. , а
, а  .
.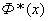 связаны между собой соотношением
связаны между собой соотношением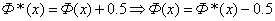
 . (10)
. (10)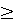 5 можно считать, что Ф(х) = 0,5);
5 можно считать, что Ф(х) = 0,5);

 . (11)
. (11) . (12)
. (12) и учитывая, что
и учитывая, что  , получим:
, получим: . (12)
. (12)


