
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В школьном курсе математики.
План. 1. Некоторые методические замечания. 2. Место и значение темы в школьном курсе математики. Изучение скалярных геометрических величин в младших классах. 3. Методические особенности изучения систем скалярных геометрических величин в средних и старших классах. 4. Различные подходы к изучению объёмов многогранников и тел вращения. 5. Методические особенности изучения площадей поверхностей тел вращения. Содержание лекции: 1. Предметом изучения данной лекции являются скалярные геометрические величины – длина, площадь, объём, мера угла. Под системой скалярных величин по А.Н. Колмогорову понимается определённое множество S={a, b, c, ….}, удовлетворяющее системе аксиом (10 аксиом). Самостоятельное задание: Выписать эти аксиомы. Любая скалярная величина по отношению к конкретному объекту обладает свойством быть измеренной, то есть охарактеризованным числом. При этом фактически задаётся соответствие между множеством фигур и множеством положительных действительных чисел так, что выполняются следующие свойства: 1) Равные фигуры имеют равные величины (инвариантность, относительно движения); 2) Величина фигуры, являющая объединением нескольких фигур без общих внутренних точек, равные сумме величин этих фигур (аддитивность); 3) Существует фигура (единичный отрезок, единичный квадрат, единичный куб), величина которого равна 1 (нормированность). Скалярные геометрические величины могут вводиться либо: 1) аксиоматически, как функции, обладающие указанными выше свойствами: а) Предполагая существование этой функции, выводят формулы для величин ломаных, многоугольников, многогранников. Показывается возможность вычисления величины произвольных многоугольных и многогранных фигур путём их разбиения на треугольники и тетраэдры и независимость их от способа разбиения, то есть ( теорема о существовании и единственности на классе многоугольных (многогранных) фигур. б) Вводится множество квадрируемых (кубируемых) фигур, спрямляемых дуг и доказывается существование и единственность рассматриваемой величины на этом множестве. 2.) конструктивно (идём в обратном направлении). Строится функция, обладающая свойствами 1) -3) с помощью описания процесса нахождения по фигуре F её величины:
1 способ: Рассматривается множество многоугольниках (многогранниках) фигур и показывается возможность их разбиения на треугольники (тетраэдры). Доказывается, что произведение основания на высоту треугольника (тетраэдра) не зависит от высоты основания. Без доказательства принимаются формулы для S треугольника и V тетраэдра. Доказывается, что введение, таким образом, функция обладает свойствами 1)-3). Далее данная функция распространяется на класс квадрируемых (кубируемых) фигур и опять доказываются указанные свойства. Данный подход редко используется в силу его психологической неубедительности (без доказательства принимаются формулы S треугольника, V тетраэдра), а также довольно сложного доказательства основных свойств площади и объёма. 1 способ: Естественный. Он позволяет ввести систему скалярных геометрических величин сразу для классов многоугольниках, многогранных фигур путём разбиения прямой, плоскости или пространства точками, прямыми или плоскостями. Получаем масштабную сетку, состоящую из квадратов со сторонами 1, 1/10, 1/100, … 1/10n. Пусть в заданной фигуре F содержится В школьных курсах основным путём введения геометрических величин является аксиоматический путь, подкрепляемый особенно на первых этапах изучения материала конструктивными соображениями, связанными с использованием транспортира, линейки, палетки и кубической масштабной сетки, как средствами измерения. Изложение теории площадей многоугольников и объёмов многогранников существенно опирается на понятие равносоставленности многоугольников и многогранников. Из свойств скалярных величин вытекает, что равносоставленные фигуры равновелики. Это позволяет ввести простой способ вычисления площадей (использовавшийся ещё Евклидом).
Укажем два важных факта, позволяющие понять логику построения соответствующего школьного материала. 1. Теорема Бойяи – Гервина: Два равновеликих многоугольника равносоставлены. Из этой теоремы вытекает, что достаточно знать формулу для S прямоугольника, чтобы легко вывести площади других многоугольников. 2. Аналогичная теорема для многогранников, сформулированная впервые Д.Гилабертом (1900 г., 3-я проблема) вообще несправедлива. Это следует из результатов Дена (1901 г.), который, в частности, показал, что правильный тетраэдр не равносоставлен с кубом того же объёма. Именно поэтому при изучении объёмов многогранников недостаточно формулы объёма прямоугольного параллелепипеда, а приходится ещё использовать неэлементарные методы для нахождения объёмов тетраэдра. Однако, для некоторых видов многогранников (например призм) рассматриваемый факт справедлив. 2. Важность линии геометрических величин определяется следующими моментами. 1) В реальной действительности мы постоянно сталкиваемся с необходимостью измерения и оценки расстояний, площадей и объёмов фигур. (Примеры подобрать самостоятельно). 2) На основе материала данной темы осуществляется знакомство школьников с важными идеями, понятиями и методами метрической геометрии, расширяются возможности применения аналитического метода. 3) Реализуются внутрипредметные и межпредметные связи на основе взаимодействия аксиоматического метода, теории действительного числа, инфинитезимальных методов (бесконечно малых), метода координат и т. д. 4) Совершенствуются вычислительные навыки, навыки тождественных преобразований и решения уравнений и неравенств. 5) На данном материале, как правило, реализуется метод опорного элемента при решении задач В школьном курсе математики изучаются следующие скалярные величины: длина отрезка, мера угла, площади многоугольника и круга, объёмы многогранников и тел вращения, длина окружности, площадь поверхности тел вращения. Изучение скалярных геометрических величин в школе осуществляется концентрически: 1 концентр – 1 – 6 классы - пропедевтический, 2 концентр – 7-11 классы – основной. 1этап. В курсе 1-4 классов у школьников развивается наглядно-интуитивное представление о величинах и их практическом измерении. Здесь они знакомятся с различными единицами измерения длины и площади, основными соотношениями между ними; измеряют и сравнивают длин отрезков и площади фигур, составленных из единичных отрезков и квадратов, с помощью линейки и палетки вычисляют периметр многоугольника, а также площадь прямоугольника (по формуле). Уже здесь учащиеся начинают производить действия с именованными числами: + и – величин, * и: величин на число, а также сравнение величин. 2 этап. В 5-6 классе представления о геометрических величинах систематизируются и углубляются. В частности, если в начальной школе отрезок и его длина воспринимаются как один и тот же объект, то в 5-ом классе учащиеся получают возможность установить различие между фигурой и её величиной, записываемой в виде числа с наименованием. Это достигается на основе сопоставления результатов выполнения двух основных задач: построения отрезка заданной длины и измерения длин данного отрезка. Если в первом случае ответ неоднозначен, то во втором результат однозначен.
При изучении площадей и объёмов реализуется тот же план, что и при изучении длин отрезков: а) определение площади и объёма не даётся, а лишь поясняется, что для величин различных поверхностей и вместимостей сосудов надо знать площадь или объём соответствующих фигур; б) на конкретных примерах вводятся свойства площадей и объёмов, единицы их измерения, обращается внимание на то, что в отличие от длины и мер углов равенство площадей или объёмов фигур вовсе не означает равенство этих фигур; в) вводятся и наглядно обосновываются формулы для площади прямоугольника и объёма прямоугольного параллелепипеда. Решаются соответствующие текстовые задачи. В 6 классе обоснование вводятся важные в практическом отношении формула для длин окружности и площади круга. 3 Основной этап изучения геометрических величин 7-11 классов. На этом этапе происходит переход от вычислительно-прикладного аспекта к формально-логическому. В учебнике А.В. Погорелова в §1 в явном виде вводятся аксиомы откладывания и измерения отрезков и углов. Вопрос об измерении отрезков и углов. Вопрос об измерении отрезков и углов в практическом плане не ставится. В учебнике Л.С. Атанасяна изложение связано с практическими измерениями. Описывается процесс измерения, на наглядном уровне поясняются свойства длины отрезков и градусных мер углов, описываются приборы для измерения расстояний и углов на местности. В аксиоматике (в Приложении 1) есть только аксиомы измерения и откладывания отрезка (аксиом измерения углов нет). Понятие о площадях и объёмах в учебнике А.В. Погорелова вводится также аксиоматически. Площадь простой фигуры (объём простого тела) – это положительная величина, численное значение которой обладает свойствами: 1)-3). В учебнике Л.С. Атанасяна и др. площадь определяется как величина части плоскости, занимаемой многоугольником, измерения площадей и объектов с помощью единичных квадратов и кубов и обосновываются основные свойства площадей и объёмов. В основу изучения площадей плоских фигур и объёмов многогранников в школьных курсах геометрии кладутся формулы S прямоугольника (S квадрата) и V прямоугольного параллелепипеда. (Можно и S треугольника и V тетраэдра и другие). Можно выделить следующие четыре подхода к изучению площадей:
1. Сравнение площадей (подход Адамара) В основе подхода - теорема о том, что площади (или объёмы) 2-х прямоугольников (прямоугольных параллелепипедов), имеющих равные основания, относятся между собой как их высоты. Данный способ обладает достаточной общностью и вместе с тем не согласуется с известными с 5-6 классов способом измерения и имеет чересчур формальный для школы характер. Этот переход использован в учебнике А.В.Погорелова. 2. Традиционный подход (учебники Килелёва, Фетисова 1957 г., Атанасяна). После рассмотрения основных допущений о площадях вводится понятие об измерении площади прямоугольника при помощи сетки квадратов последовательно для случаев, когда обе стороны выражаются через единичный отрезок как: 1.) натуральное число; 2.) конечная десятичная дробь (рациональное число); 3.) бесконечная десятичная дробь (иррациональное число). 3. В 3-ем наиболее сложном случае площадь определяется либо как предел последовательности площадей прямоугольников, длины сторон которого выражаются рациональными числами, либо через введение двух последовательностей приближённых рациональных значений площади по недостатку и по избытку. 4. (на основе равносоставленности) – учебник Глагольева, 1954 г. В явном виде рассматривается понятие равносоставленности. Определяются условия, при которых параллелограммы и прямоугольники равносоставлены. Рассматривается вывод формулы площади прямоугольника (прямоугольного параллелепипеда) для натуральных и рациональных измерений, а для иррациональных измерений формулы даются без доказательства. Данный подход также громоздок и не обладает достаточной психологической убедительностью в силу последнего допущения. Наиболее оптимальным в настоящее время учителя считают классический подход (2-й подход) без рассмотрения третьего случая, либо принятие формулы площади квадрата за аксиому. После доказательства (вывода) формулы площади прямоугольника, пользуясь элементарными методами (теоремой Бойяи-Гервина – 12 равновеликих многоугольника равносоставлены) выводят формулы для площадей остальных прямоугольников, либо разбивая, либо дополняя новый многоугольник. В основе изложения теории объёмов многогранников лежит формула для объёма прямоугольного параллелепипеда, доказываемая совершенно аналогично формуле для площади прямоугольника. В силу равносоставленности равновеликих призм вывод формул для объёмов наклонных параллелепипедов и призм можно осуществить элементарными методами. Соответствующие соображения иллюстрируются на наглядных моделях, а выводы аналогичны тем, которые применялись в планиметрии. Основная методическая проблема при выводе формул для объёмов многогранников является соответствующая формула для тетраэдра (теорема Дена). По этой теореме для вывода этой формулы необходимо использовать неэлементарные методы, связанные с операцией интегрирования (явно или неявно). Подход, при этом используемый, как правило, отражается и на методике изложения теории объёмов тел вращения.
1 подход – метод исчерпывания («чёртова лестница») (учебники Киселёва, Погорелова) осуществляется в двух вариантах: Первый вариант - косвенный. 1 этап – лемма. Две треугольные пирамиды с равными площадями оснований и равными высотами равновелики. Разбив высоту на n частей, проводим плоскости, параллельные плоскости основания. Получим разбиение пирамид на слои. Через вершины сечений призмы проводим n прямых, параллельных какому – либо ребру призмы. Получаем два ступенчатых многогранника, состоящих из входящих в первую пирамиду и содержащих эту пирамиду призм. Их суммарные объёмы отличаются на объём призмы последнего от вершины слоя S
(см. п. 198 учебник Погорелова) Аналогично: V2 2 этап: Треугольная пирамида дополняется до призмы путём присоединения к ней ещё двух пирамид. Все три пирамиды по предыдущей лемме – равновелики Второй вариант – прямой. (уч. Глаголева) является модификацией предыдущего варианта. 1 этап: Для пирамиды строится двоякая последовательность призм. Показывается, что Vпирамиды является общим пределом последовательности объёмов ступенчатых многогранников при неограниченном увеличении количества составляющих призм:
Значит, достаточно вычислить объём ступенчатой фигуры. 2 этап: Объём ступенчатой фигуры вычисляется как сумма объёмов и подобных призм. 2 вариантпсихологически убедительней, но требует дополнительного времени для формул суммы квадратов натуральных чисел. Объёмы тел вращения при данном подходе определяются как пределы соответствующих последовательностей объёмов вписанных и описанных многогранников (призм и пирамид). Основную сложность в данном случае составляет вычисленные объёмы шара. Здесь приходится вводить формулу для объёма тела вращения через определённый интеграл. Третий подход – вычисление объёмов тел с помощью определённого интеграла (уч. Атанасяна и Александрова). 1 Для объёма простого тела рассматривается общий подход: V= где S (х) – площадь сечения тела плоскости, перпендикулярной оси абсцисс. 2.) Объём наклонной призмы и пирамиды. 3.) Объёмы тел вращения. Четвертый подход – через принцип Кавальери (итальянский математик 17 века, аббат монастыря). Две фигуры с равными высотами равновелики, если равны любые их сечения, приведённые параллельно основаниям на одинаковой высоте от них. Данный принцип принимается за дополнительную аксиому объёмов (для площадей и объёмов).
Для объёмов – аналогично. 1 вариант. Из принципа Кавальери напрямую следует лемма о равновеликости пирамид, и таким образом, существенно облегчается вывод для объёма пирамиды; можно вычислить и объёмы тел вращения. В частности при выводе формулы Vшара рассматривается полушар и конус, вписанный в центр. Площади сечений полушара и второй фигуры равны:
2 вариант. Вычисление объёма пирамиды (Виленкин) а) V куба = 8 Н 3 V пир = б) Берём произвольную пирамиду с площадью основания S и выстой Н. По принципу Кавальери объём 4-угольной правильной пирамиды и данной равны. Следовательно, формула верна для любой пирамиды. Данный подход в настоящее время считается наиболее приемлемым в силу достаточной простоты (предельный переход уходит в доказательство принципа Кавальери). Четвертый подход – формула Симпсона (Том Симпсон – английский математик 18 века). Если в пространственной фигуре основания параллельны и площади сечений, параллельны основанию, удовлетворяют условию S(х) = ах2 + вх + с, где S (х) – функция от расстояния между сечением и основанием фигуры, то объём фигуры может быть найден по формуле: V = где Н – высота, Q0 и Q – площади оснований, Qср – площадь среднего сечения. Для конуса, пирамиды Q = 0, для шара Q0 =Q=0, а плоскость оснований считаются параллельными. Доказательство формулы Симпсона достаточно громоздкое и, как правило, опускают. (На основе интегральной формулы: V = Достоинства метода – его универсальность, недостаток – формальное введения. Самостоятельное задание: Выписать формулы для сечений конуса, шара, пирамиды и цилиндра как функций от расстояния между сечением и основанием фигуры. Sсеч. пир. = 5. Площадь поверхностей фигур вращения в школе могут рассматриваться на различных уровнях строгости в зависимости от авторских установок и специфики контингента. 1. Общий подход по Минковскому (немецкий математик). Площадь произвольной выпуклой поверхности определяется таким образом:
наглядно предоставляемый как двойной слой толщиной 2h, покрывающий с обеих сторон. Далее на основе соответствующего определения вводились формулы для площади поверхности шара, конуса и цилиндра. Данный подход был использован в ранних изданиях учебника Погорелова и не оправдал себя в силу формального характера и необходимости применения довольно изощренных оценок. (см. В. Дубровский Площадь поверхности по Минковскому – Квант 1979, № 4.) 2. Основан на идеи исчерпывания (уч. Киселёва, Погорелова (новое издание)). Цилиндры и конусы «исчерпываются» призмами и пирамидами, а поверхность сферы рассматривается через поверхность, полученную при вращении ломаной, вписанной в большую полуось круга. Тогда площадь этой поверхности будет равна пределу площади поверхности тела при неограниченном увеличении сторон ломаной. По доказанной ранее лемме Sn = 2π Для шара 3. Основан на развёртках (уч. Атанасяна). При этом используется допущения о сохранении величин площади при «развёртывании» поверхности вращения. Данный подход неприемлем для площади поверхности сферы, не имеющей плоской развёртки. Однако, в некоторых учебниках (Погорелов) сделана попытка приближенного представления участков сферы в виде многоугольников, являющихся гранями многогранника, описанного около сферы. 4. Формальный подход. За площадь поверхности фигуры, полученной при вращении вокруг оси ОХ графика функции у = f (х), имеющей на S = 2 π В учебнике А.В. Погорелова используется модификация подходов 2 и 3, взяв за основу идею исчерпывания шара пирамиды с вершиной в центре шара с последующим предельным переходом, соответствующим неограниченному уменьшению размеров граней многогранника, описанного около шара.
Vвпис. ш.
площадь поверхности 4π R2 4π R2
Задание для самостоятельной работы. Выписать систему аксиом для определения систем скалярных величин по А.Н. Колмагорову их учебного пособия (4). Вопросы для самопроверки: 1. Перечислите основные скалярные геометрические величины, изучаемые в школьном курсе. 2. Что такое величина? Какими свойствами обладает любая скалярная величина? 3. В чём суть аксиоматического введения скалярных геометрических величин и конструктивного? И какой путь является основным в школьном курсе? 4. Какую роль играет понятие равносоставленности в теории площадей и объектов? 5. Каковы основные цели изучения линии геометрических величин в школьном курсе? 6. Что известно учащимся о геометрических величинах из пропедевтического курса математики? 7. Каковы методические подходы к изучению длин отрезков в школьном курсе? 8. Какие 4 основных подхода можно выделить при изучении площадей в школьном курсе геометрии? Суть каждого из этих подходов? 9. Какие подходы используются в основной школе при изучении длины окружности и площади круга? 10. В чём суть метода исчерпывания при построении теории объёмов многогранников? 11. Интегральный подход к нахождению объёмов геометрических тел. 12. Нахождение объёмов с помощью принципа Кавальери и формулы Симпсона. 13. Каковы возможные подходы к построению теории площадей поверхностей тел вращения в школьном курсе? Литература: 4, 6, 7, 10, 14, 16, 17.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.102.225 (0.069 с.) |
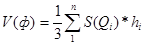 )
) ln квадратов со стороны 1|10n , а сама фигура F содержится в bn квадратов со стороны 1/10n. Положим за Sln - число ln/10n, за S bn – число bn/10n (число единиц площади, содержащихся в F и содержащих F). Если существует единственное число, заключённое между всеми числами Sln и всеми числами Sbn, то фигура F называется квадрируемой (кубируемой). Для отрезков получается что-то типа теории сечений. Дедекинда (теория действительного числа).
ln квадратов со стороны 1|10n , а сама фигура F содержится в bn квадратов со стороны 1/10n. Положим за Sln - число ln/10n, за S bn – число bn/10n (число единиц площади, содержащихся в F и содержащих F). Если существует единственное число, заключённое между всеми числами Sln и всеми числами Sbn, то фигура F называется квадрируемой (кубируемой). Для отрезков получается что-то типа теории сечений. Дедекинда (теория действительного числа).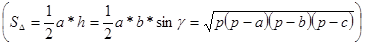
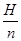 (S - площадь основания, H - высота, n -номер слоя).
(S - площадь основания, H - высота, n -номер слоя).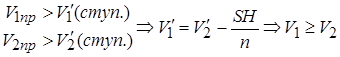 , (n – любое
, (n – любое 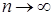 )
)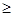 V1
V1 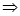 V2= V1
V2= V1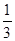 Vпризмы
Vпризмы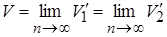
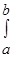 S (х) dx,
S (х) dx,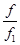 =
= 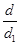 =
= 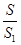
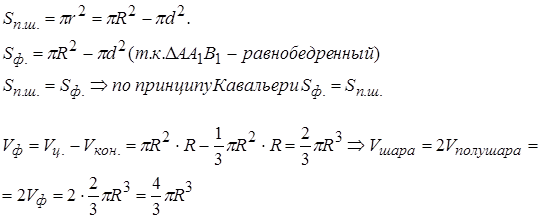
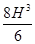 =
= 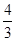 Н 3 = 4 Н 2
Н 3 = 4 Н 2 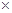
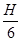 (Q0 + 4Qср + Q),
(Q0 + 4Qср + Q),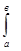 Q (х) dх (кв. ед.) (см. уч. Ю.М. Колягина).
Q (х) dх (кв. ед.) (см. уч. Ю.М. Колягина).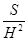
 х2 , Sсеч ш. = (R2 – х2), Sсеч цил. = πR2.
х2 , Sсеч ш. = (R2 – х2), Sсеч цил. = πR2.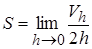 , где Vh – объём фигуры Fh ,
, где Vh – объём фигуры Fh ,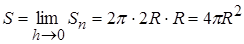
 а, b
а, b 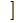 непрерывную произвольную, принимается число:
непрерывную произвольную, принимается число: dх
dх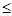 Vмногогр.
Vмногогр. 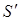 R
R 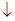
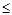
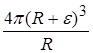 , при ε
, при ε  0
0


