
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 1 основні поняття математичної фізики. диференціальні рівняння з частинними похіднимиСтр 1 из 17Следующая ⇒
Вступ
Мета цього посібника – допомогти студентам глибше засвоїти матеріал таких спеціальних розділів, як „Рівняння ма-тематичної фізики” та „Операційне числення”. Математична фізика, як теорія математичних моделей фізичних явищ, займає особливе місце як у математиці, так і у фізиці. Перебуваючи на стику цих наук, математична фізика тісно зв'язана з фізикою в тій частині, яка стосується побудови математичної моделі, і в той самий час математична фізика – розділ математики, оскільки методи дослідження моделей є математичними. Наприкінці XVII століття методи математичної фізики як теорії математичних моделей почали інтенсивно розроблятися в працях І. Ньютона щодо створення основ класичної механі-ки, всесвітнього тяжіння, теорії світла. Подальший розвиток методів математичної фізики (XVIII – перша половина XIX століття) і їхнє успішне застосування до вивчення математич-них моделей величезного обсягу різних фізичних явищ пов'я-зані з іменами Ж. Лагранжа, Л. Ейлера, П.Лапласа, Ж. Фур’є, К. Гауса, Б. Рімана, М. Остроградського та інших учених. Великий внесок у розвиток методів математичної фізики зробили О. Ляпунов та В. Стєклов. З другої половини XIX століття методи математичної фізики успішно використовува-лися для вивчення математичних моделей фізичних явищ, пов'язаних з різними фізичними полями і хвильовими функ-ціями в електродинаміці, акустиці, теорії пружності, гідро- й аеродинаміці та інших напрямах дослідження фізичних явищ у суцільних середовищах. Математичні моделі цього класу явищ найчастіше описуються за допомогою диференціальних рівнянь з частинними похідними, що одержали назву рівняння математичної фізики. У зв'язку з бурхливим розвитком електронної та обчислю-вальної техніки особливе значення для дослідження матема-тичних моделей фізики набувають прямі чисельні методи, і в першу чергу скінченно-різницеві методи розв’язування крайо-вих задач, що дозволило методами математичної фізики ефек-тивно вирішувати нові задачі газової динаміки, теорії перено-су, фізики плазми, у тому числі і зворотні задачі цих напрям-ків фізичних досліджень. Поряд із традиційними розділами математики стали широко застосовуватися теорія операторів, теорія узагальнених функцій, теорія функцій багатьох комп-лексних змінних, топологічні і алгебраїчні методи. Інтенсивна взаємодія теоретичної фізики, математики і використання комп’ютерів у наукових дослідженнях, привела до значного розширення математики, створення нових класів моделей і піднесла на новий рівень сучасну математичну фізику.
Постановка задач математичної фізики полягає в побудові математичних моделей шляхом виведення диференціальних, інтегральних або алгебраїчних рівнянь, що характеризувати-муть відповідний фізичний процес та описуватимуть основні закономірності досліджуваного класу явищ. При цьому вихо-дять з основних фізичних законів, що враховують тільки най-істотніші риси явища, відкидаючи низку його другорядних характеристик. Ефективним способом розв’язування диференціальних рівнянь з частинними похідними є викори-стання операційних методів, зокрема перетворення Лапласа. Теоретичний матеріал цих розділів можна знайти в підручниках [1–6], тому даний конспект лекцій містить у вигляді довідкового матеріалу в рамках робочої програми для спеціальностей нафтогазової справи лише ті короткі відомості з теорії, які безпосередньо застосовуються при розв’язуванні задач. Посібник буде корисним як студентам, так і викладачам, які ведуть практичні заняття з курсу математичної фізики.
Лекція 1 основні поняття математичної фізики. диференціальні рівняння з частинними похідними
Рисунок 2.2 – Стержень, один з кінців якого закріплений, а другий – вільний
Дійсно так, бо для закріпленого кінця характерним є те, що зміщення його весь час дорівнює нулю, а для вільного кінця – те, що у перерізі 2) Нехай один кінець стержня закріплений жорстко, а до вільного кінця (
Рисунок 2.3 – Один кінець стержня жорстко закріплений, а на другий – діє сила Р
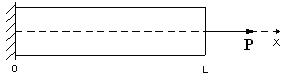
3) Нехай обидва кінці стержня жорстко закріплені (Рисунок 2.4). Тоді:
Рисунок 2.4 – Обидва кінці стержня жорстко закріплені
4) Нехай один кінець стержня (
Тоді, враховуючи, що сила в’язкого опору пропорційна швидкості руху, і записуючи умову рівноваги на правому кінці, маємо:
Рисунок 2.5 – На правому кінці стержня має місце в’язкий опір
5) Нехай один кінець стержня (
Рисунок 2.6 – Один кінець стержня жорстко закріплено, а до іншого приєднано вантаж маси М
6) Нехай один кінець стержня (
Рисунок 2.7 – Один кінець стержня закріплено жорстко, а другий – пружно
Задача 2.1 Стержень довжини l, один кінець якого жорстко закріплено, перебуває у стані спокою. У деякий момент часу (
Розв’язком цієї задачі є функція Задача 2.2 Поставити задачу про поздовжні коливання стержня, один кінець якого жорстко закріплено, а до вільного кінця прикладено силу P, причому в момент часу
Зінтегрувавши останнє рівняння по змінній х у межах від 0 до х, отримаємо:
Зауважимо, що тут коливання виникають у момент зняття сили Р. Розв’язком цієї задачі є функція Задача 2.3 Верхній кінець вертикального підвішеного важкого стержня прикріплено до стелі ліфта, який вільно падає, причому досягши швидкості V, він раптово зупиняється. Поставити задачу про поздовжні коливання стержня.
Розв’язком цієї задачі є функція Контрольні запитання 2.1 Які припущення відносно геометричного та фізичного стану стержня слід зробити при виведенні рівняння, яке б описувало поздовжні коливання, що виникають у ньому під час розтягу або стиску внаслідок прикладених зусиль? 2.2 На які фізичні закони спираються при виведенні хвильово- го рівняння, що описує поздовжні коливання стержня? 2.3 Вигляд хвильового рівняння у випадку важкого стержня. 2.4 З чого складається постановка задачі математичної фізики про поздовжні коливання стержня?
2.5 Що задають та характеризують початкові умови? 2.6 На що вказують крайові умови? Різновиди крайових умов.
Рисунок 3.2 – Початкова форма струни
Зауважимо, що при отриманні першої початкової умови можна скористатися рівнянням прямої, яка проходить через дві точки:
Зауваження. 1) Хвильове рівняння характеризує не тільки процеси поздовжніх коливань стержня і поперечних коливань струни. Воно є універсальною математичною моделлю для всіх коливальних процесів різної фізичної природи. Так, хвильове рівняння описує електричні коливання, крутильні коливання валу, акустичні коливання пружного газу тощо. 2) Також хвильове рівняння можна поширити на коливальні процеси, які відбуваються не лише в одновимірному просторі, як у випадках зі стержнем чи струною, але й у двовимірному та тривимірному просторі. Так, хвильове рівняння, що моделює вільні поперечні коливання плоскої мембрани у формі області
А тривимірна модель коливального процесу в деякій просторовій області
Таке рівняння описує, наприклад, закон поширення світлових та електромагнітних хвиль у просторі. Фізичний зміст сталої а у хвильовому рівнянні – це швидкість розповсюдження хвиль у відповідних хвильових процесах. Контрольні запитання 3.1 При яких припущеннях виведено хвильове рівняння для поперечних коливань струни? 3.2Що визначає функція 3.3Як вільний член у хвильовому рівнянні 3.4 У чому полягає фізичний зміст коефіцієнта 3.5 З чого складається постановка задачі про поперечні коливання струни? 3.6 Чим задають початкову форму струни і початкові швидкості точок струни? 3.7 Що відображають крайові умови? 3.8 Що є визначальним у постановці задачі про поперечні коливання нескінченної струни?
Рисунок 4.1 – Початкова форма струни
Згідно з нашою постановкою функції
Нульові члени можна виключити, якщо ввести заміну n =2 m -1, (m =1, 2, 3,...). Тоді
Вимушені коливання струни Задача про вимушені коливання скінченної струни довжини l зводиться до інтегрування неоднорідного диференціального рівняння:
при заданих додаткових умовах:
П.У.
Тут функція Як і при розв’язуванні звичайних неоднорідних диференціальних рівнянь, розв’язок рівняння (4.13) можна шукати як суму двох функцій:
перша з яких
при умовах: П.У.
а друга функція
при однорідних умовах
П.У.
Функція Функція
відповідної однорідної задачі, тобто візьмемо:
де функції Крайові умови для функції
Підставляючи функцію
З метою подальших перетворень розглянемо функцію
де
Щоб рівняння (4.18) задовольнялося, досить накласти вимогу, щоб коефіцієнти при синусах були однакові:
Для визначення
П.У. Розв’язок рівняння (4.19) можна шукати методом варіації довільних сталих. Таким чином, визначивши функції
Приклад 4.3 Знайти коливання важкої струни із закріпленими кінцями, яка в початковий момент часу
П.У. Шукаємо розв’язок згідно наведеної методики у вигляді:
Знайдемо складові 1) Постановка задачі для
при умовах: П.У. Знайдемо розв’язок цієї задачі за методом Фур’є:
де
Тоді розв’язок:
3) Постановка задачі для
П.У.
Шукатимемо функцію
Підставимо цю функцію в рівняння:
Розкладемо вільний член
де
Отже,
Для
Прирівнюючи коефіцієнти при синусах, отримаємо:
Виключимо нульові значення в правій частині. Для цього достатньо ввести заміну нумерації:
Тоді
при початкових умовах:
П.У.
Одержали лінійне диференціальне рівняння другого поря-дку із спеціальною правою частиною. Розв’язок шукаємо у вигляді:
де
Розв’язавши характеристичне рівняння
маємо:
Тоді загальний розв’язок
Частинний розв’язок неоднорідного рівняння Для знаходження невідомої сталої
Звідси
Тоді
Отже,
Знайдемо
Тоді
Відповідь:
Контрольні запитання
4.1 Який метод застосовують для розв’язування задач про вільні поперечні коливання нескінченої струни? 4.2 Який метод застосовують для розв’язування задач про вільні поперечні коливання скінченної струни? 4.3 Суть методу Фур’є для розв’язування задач на коливання. 4.4 У чому полягає фізичний зміст розв’язку задачі про поперечні коливання? 4.5 У чому полягає задача про вимушені коливання струни?
Зауваження Розглянемо випадок, коли на кінцях стержня задається ненульова температура. Тоді задача має наступну постановку:
П.У.
Тут У цій задачі з неоднорідними граничними умовами достатньо зробити підстановку:
яка зведе її до попередньої задачі відносно функції Розглянемо ще одну задачу про поширення тепла у стержні. 2) Знайти розподіл температур в стержні, на одному кінці якого весь час підтримується нульова температура, а другий кінець теплоізольвано при довільній початковій умові. Поставимо задачу:
П.У. U(x,0)=φ(x), К.У.
Зазначимо, що тут не суттєво, який кінець теплоізольовано. Як бачимо, крайові умови однорідні. Розв’яжемо цю задачу за методом Фур’є, згідно якого
Тоді рівняння теплопровідності:
або
Розглянемо рівняння
розв’язок якого Сталі А та В шукаємо із крайових умов:
К.У.
Розпишемо граничні умови:
Очевидно, що Звідси Отже,
Розв’яжемо друге рівняння для функції
Розв’язок цього рівняння:
Враховуючи, що
Отже, маємо
Поклавши
Коефіцієнти
Отже, формули (6.30) і (6.31) дають розв’язок даної задачі. 3) Розв’язати задачу про поширення тепла в стержні, на одному кінці якого стала температура U0, а другий – теплоізольований. Поставимо задачу:
П.У. U(x,0)=φ(x), К.У. За методом Фур’є крайові умови мають бути нульовими. Тому проведемо заміну
Рівняння теплопровідності:
К.У.
П.У.
За методом Фур’є отримаємо
де
Отже, остаточно маємо: Приклад 6.2 Розв’язати задачу про поширення тепла у стержні довжиною l, на кінцях якого весь час підтримується нульова температура, а початковий розподіл температур задається функцією
П.У.
Згідно з методом Фур’є ця задача має розв’язок:
де Як відомо, система власних функцій
Таким чином, усі коефіцієнти
Тоді розв’язок задачі запишемо так
Задача Діріхле
Ця задача (перша крайова задача) у просторі формулюється так: знайти функцію
К.У.
Очевидним можна вважати той факт, що задача Діріхле завжди має розв’язок. Дійсно, якщо, наприклад, кожна точка на поверхні тіла постійно підтримується при певній заданій температурі (яка може бути різною у різних точках поверхні), то у кожній точці тіла встановиться своя температура, яка і дає розв’язок задачі Діріхле при заданих крайових умовах. Також очевидно, що цей розв’язок буде єдиним. Аналогічно формулюється задача Діріхле у двовимірному випадку: знайти функцію
К.У.
Зазначимо, що задача Діріхле розв’язується дуже просто в одновимірному випадку, коли розглядається, наприклад, стаціонарний розподіл температури у тонкому стержні довжи-ни l з теплоізольованою бічною поверхнею. Тоді задача Діріхле ставиться так: знайти функцію
К.У.
Задача Діріхле у цьому випадку має розв’язок
Задача Неймана
задача Неймана (друга крайова задача)формулюється так: знайти функцію К.У. Нагадуємо, що похідна Мішана задача Мішана задача (третя крайова задача) формулюється так: знайти функцію
К.У. де функції ють задачею з косою похідною.
Задача діріхле для круга
Нехай у площині хоу є круг радіуса R з центром в початку координат. на його колі задана деяка функція
К.У. Припустимо, що
Будемо шукати розв’язок за методом Фур’є, подаючи функцію
Підставляючи її в рівняння та враховуючи, що
Відокремимо змінні:
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.143.4 (0.314 с.) |
 (2.11)
(2.11)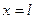 пружна сила
пружна сила  . Отже,
. Отже,  . Звідси
. Звідси 
 (2.12)
(2.12)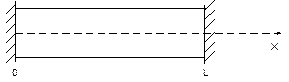
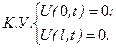 (2.13)
(2.13) ) жорстко закріп-лений, а на другому кінці (
) жорстко закріп-лений, а на другому кінці (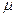 (Рисунок 2.5).
(Рисунок 2.5).
 (2.14)
(2.14)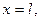 маємо:
маємо:
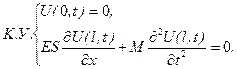 (2.15)
(2.15) маємо:
маємо: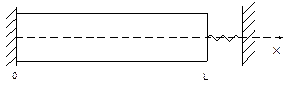
 (2.16)
(2.16) ) до його вільного кінця прикладено силу Q, напрямлену вздовж осі стержня. Сформулювати задачу про поздовжні коливання стержня.
) до його вільного кінця прикладено силу Q, напрямлену вздовж осі стержня. Сформулювати задачу про поздовжні коливання стержня. Щоб поставити задачу, потрібно записати диференціальне рівняння, яке моделює даний фізичний процес, а також початкові та крайові умови, які відображають специфіку цієї задачі. Вважаємо, що стержень перебуває у стані спокою. Коливання виникають у момент прикладання сили Q до вільного кінця, отже,
Щоб поставити задачу, потрібно записати диференціальне рівняння, яке моделює даний фізичний процес, а також початкові та крайові умови, які відображають специфіку цієї задачі. Вважаємо, що стержень перебуває у стані спокою. Коливання виникають у момент прикладання сили Q до вільного кінця, отже,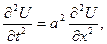

 ,
,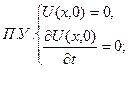

 класу
класу  .
. 
 ,
, 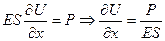 .
. . Тоді постановка задачі має вигляд:
. Тоді постановка задачі має вигляд:




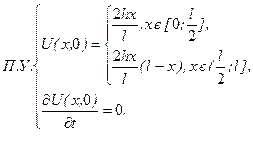
 .
. 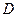 , має вигляд:
, має вигляд: ,
,  . (3.8)
. (3.8) має такий вигляд:
має такий вигляд: ,
, 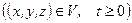 . (3.9)
. (3.9) , яка є розв’язкомхвильового рівняння
, яка є розв’язкомхвильового рівняння  для поперечних коливань струни?
для поперечних коливань струни? впливає на характер коливань (вільні коливання чи вимушені)?
впливає на характер коливань (вільні коливання чи вимушені)? у хвильовому рівнянні для поперечних коливань струни?
у хвильовому рівнянні для поперечних коливань струни? Постановка задачі буде наступною:
Постановка задачі буде наступною:

 ,
,  . Отже, у (4.12) коефіцієнт
. Отже, у (4.12) коефіцієнт  . Знайдемо коефіцієнт
. Знайдемо коефіцієнт  :
:



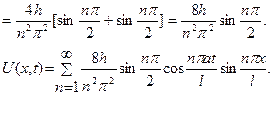

 ,
,  К.У.
К.У. 
 є заданою у всій розглядуваній області.
є заданою у всій розглядуваній області. (4.14)
(4.14) задовольняє однорідне рівняння
задовольняє однорідне рівняння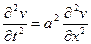 ,
,  К.У.
К.У. 
 задовольняє неоднорідне рівняння
задовольняє неоднорідне рівняння ,
,  К.У.
К.У. 

 , (4.17)
, (4.17) підлягають визначенню.
підлягають визначенню. задовольняють їх. Щоб задовольнити і початкові умови, досить покласти:
задовольняють їх. Щоб задовольнити і початкові умови, досить покласти:
 .
. . (4.18)
. (4.18) як функцію однієї змінної
як функцію однієї змінної  (тобто
(тобто  вважатимемо параметром). Припустимо, що функцію
вважатимемо параметром). Припустимо, що функцію 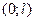 в ряд Фур’є за синусами як функцію однієї змінної
в ряд Фур’є за синусами як функцію однієї змінної  ,
, .
. . (4.19)
. (4.19)
 .
. перебувала в стані спокою і мала форму
перебувала в стані спокою і мала форму  .
. ,
,  ,
,  К.У.
К.У. 
 ,
,  К.У.
К.У. 
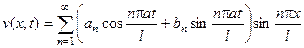 ,
,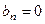 ,
, для всіх
для всіх  , а для
, а для  :
: .
.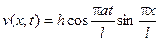 .
.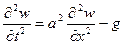 ,
,  .
. в ряд Фур’є за синусами:
в ряд Фур’є за синусами: ,
,
 .
. .
. .
. ,
, 
 ,
,
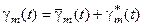 ,
, – загальний розв’язок відповідного однорідного рівняння:
– загальний розв’язок відповідного однорідного рівняння: .
. ,
, .
. .
. , враховуючи праву частину, шукаємо у вигляді:
, враховуючи праву частину, шукаємо у вигляді:  .
. підставимо
підставимо  .
. .
. .
. .
. і
і  із початкових умов:
із початкових умов:
 ;
; .
.

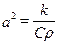 ,
,  К.У.
К.У. 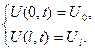 (6.24)
(6.24) та
та  – сталі температури відповідно на кінцях х= 0 та x=l.
– сталі температури відповідно на кінцях х= 0 та x=l.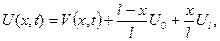 (6.25)
(6.25) Цю процедуру пропонується виконати студентам самостійно.
Цю процедуру пропонується виконати студентам самостійно.
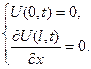 (6.26)
(6.26) (6.27)
(6.27)

 ,
,
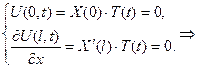


 тоді
тоді 
 ,
, 
 . (6.28)
. (6.28) , що одержується з рівняння теплопровідності:
, що одержується з рівняння теплопровідності: .
.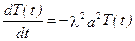
 .
. .
.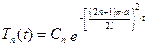 . (6.29)
. (6.29)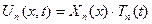 і розв’язок даної зада-чі шукаємо у вигляді:
і розв’язок даної зада-чі шукаємо у вигляді:
 , остаточно будемо мати:
, остаточно будемо мати: . (6.30)
. (6.30)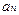 визначаються із початкової умови, як у попередній задачі:
визначаються із початкової умови, як у попередній задачі: (6.31)
(6.31) (6.32)
(6.32)


 (6.33)
(6.33)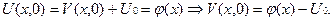
 (6.34)
(6.34)

 К.У.
К.У. 


 є ортогональною на проміжку
є ортогональною на проміжку 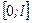 , тобто
, тобто коли
коли  , і не дорівнює нулю, коли
, і не дорівнює нулю, коли  .
.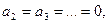 проте коефіцієнт
проте коефіцієнт 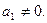 Знайдемо його:
Знайдемо його:
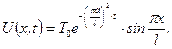
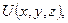 яка задовольняє всередині замкненої поверхні
яка задовольняє всередині замкненої поверхні 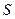 рів-няння Лапласа
рів-няння Лапласа  та набуває у кожній точці М поверхні
та набуває у кожній точці М поверхні 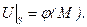 (6.37)
(6.37) яка задовольняє всередині замкненої кривої Г рівняння Лапласа
яка задовольняє всередині замкненої кривої Г рівняння Лапласа  та набуває у кожній точці М кривої Г заданих значенень:
та набуває у кожній точці М кривої Г заданих значенень: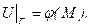 (6.38)
(6.38) яка задовольняє рівняння Лапласа для усіх
яка задовольняє рівняння Лапласа для усіх 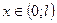 і набуває на кінцях стержня заданих значенень:
і набуває на кінцях стержня заданих значенень: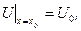
 (6.39)
(6.39) (6.40)
(6.40)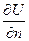 у кожній точці М поверхні
у кожній точці М поверхні 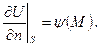 (6.41)
(6.41) яка задовольняє всередині замкненої поверхні
яка задовольняє всередині замкненої поверхні 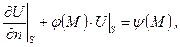 (6.42)
(6.42) та
та 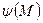 є заданими. Цю задачу ще назива-
є заданими. Цю задачу ще назива- де
де  – полярний кут. Треба знайти функцію
– полярний кут. Треба знайти функцію  неперервну у крузі, яка задовольняє всередині круга рівнянню Лапласа [1]. Постановка задачі в полярних координатах має вигляд:
неперервну у крузі, яка задовольняє всередині круга рівнянню Лапласа [1]. Постановка задачі в полярних координатах має вигляд: ,
,  ,
,
 можна розкласти в ряд Фур’є на
можна розкласти в ряд Фур’є на  . Перепишемо рівняння Лапласа, домноживши його на
. Перепишемо рівняння Лапласа, домноживши його на 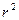 :
:
 у вигляді добутку двох функцій, кожна з яких залежить від однієї змінної:
у вигляді добутку двох функцій, кожна з яких залежить від однієї змінної: (6.48)
(6.48) та
та  отримаємо:
отримаємо:



