
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики оценки измеряемой величины
Задачей измерения является нахождение по полученным наблюдениям наилучшей оценки измеряемой величины - результата измерения и оценки точности этого результата, т.е. степени его близости к истинному значению величины - погрешности измерений. При этом считается, что закон распределения наблюдений и погрешностей известен. Под оценкой в данном случае понимается нахождение значений параметров этих распределений случайных величин по ограниченному числу наблюдений. Полученные оценки параметров распределений являются лишь приближениями к истинным значениям этих параметров и используются в качестве результата измерений и его погрешности. Для того чтобы оценку, получаемую по результатам многократных наблюдений, можно было использовать в качестве параметра функции распределения случайной величины, она должна отвечать ряду требований — быть состоятельной, несмещенной и эффективной. Состоятельная оценка – это оценка, которая при увеличении числа наблюдений стремится к истинному значению оцениваемого параметра. Несмещенная оценка - оценка, математическое ожидание которой равно истинному значению оцениваемого параметра. Эффективная оценка – оценка, имеющая наименьшую дисперсию по сравнению с любой другой оценкой данного параметра. Методы нахождения оценок параметров распределений, а по ним результатов измерений и их погрешностей зависят от вида функции распределения и от тех соглашений по обработке результатов измерений, которые нормируются в рамках законодательной метрологии в нормативной документации. Примеры распределения случайных величин Способы нахождения значений случайной величины зависят от вида функции ее распределения. Однако на практике такие функции, как правило, неизвестны. Если же случайный характер результатов наблюдений обусловлен погрешностями измерений, то полагают, что наблюдения имеют нормальное распределение. Это обусловлено тем, что погрешности измерений складываются из большого числа небольших возмущений, ни одно из которых не является преобладающим. Согласно же центральной предельной теореме сумма бесконечно большого числа взаимно независимых бесконечно малых случайных величин с любыми распределениями имеет нормальное распределение. Нормальное распределение для
случайной величины х с математическим ожиданием 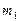 и дисперсией s имеет вид: и дисперсией s имеет вид:
Реально даже воздействие ограниченного числа возмущений приводит к нормальному распределению результатов измерений и их погрешностей. В настоящее время наиболее полно разработан математический аппарат именно для случайных величин, имеющих нормальное распределение. Если же предположение о нормальности распределения отвергается, то статистическая обработка наблюдений существенно усложняется и в таком случае невозможно рекомендовать общую методику статистической обработки наблюдений. Часто даже не известно, какая характеристика распределения может служить оценкой истинного значения измеряемой величины. Выше приведено аналитическое выражение нормального распределения для случайной измеряемой величины х. Переход к нормальному распределению случайных погрешностей Нормальное распределение характеризуется двумя параметрами: математическим ожиданием m1 и средним квадратическим отклонением σ. При многократных измерениях несмещенной, состоятельной и эффективной оценкой m1 для группы из n наблюдений является среднее арифметическое
Нужно сказать, что среднее арифметическое дает оценку математического ожидания результата наблюдений и может быть оценкой истинного (действительного) значения измеряемой величины только после исключения систематических погрешностей. Оценка S среднего квадратического отклонения (СКО) дается формулой: Эта оценка характеризует рассеяние единичных результатов измерений в ряду равноточных измерений одной и той же величины около их среднего значения. Другими оценками рассеяния результатов в ряду измерений являются размах (разница между наибольшим и наименьшим значением), модуль средней арифметической погрешности (арифметическая сумма погрешностей, деленная на число измерений) и доверительная граница погрешности (подробно рассматривается ниже).
СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:
Оценка S характеризует рассеяние единичных результатов наблюдений относительно среднего значения, то есть в случае, если мы за результат измерений примем отдельный исправленный результат наблюдений. Если же в качестве результата измерений принимается среднее арифметическое, то СКО этого среднего
Нормальное распределение погрешностей имеет следующие свойства: 1. симметричность, т.е. погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто; 2. математическое ожидание случайной погрешности равно нулю; 3. малые погрешности более вероятны, чем большие; 4. чем меньше s, тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей. Другим распространенным в метрологии распределением случайной величины является равномерное распределение - распределение, при котором случайная величина принимает значения в пределах конечного интервала от х1 до х2 с постоянной плотностью вероятностей. Дифференциальная функция равномерного распределения имеет вид: f(x) = с при х1 £ x £ х2 f(x) = 0 при х2 < x < х1 При нормировке площади кривой распределения на единицу, получаем, что с(х2 – х1) = 1 и с = 1/ (х2 – х1).
Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона. В настоящем курсе они не рассматриваются. Доверительные интервалы Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов. Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с доверительной вероятностью Р, если площадь кривой распределения между абсциссами – Δх и + Δх составляет Р -ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р ×100% всех возможных значений случайной погрешности. Доверительный интервал для нормального распределения находится по формуле:
где коэффициент t зависит от доверительной вероятности Р. Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999). Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверительные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.
При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:
где tq – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q -процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P; Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действительного) значения измеряемой величины, оценкой которой является среднее арифметическое Недостатком доверительных интервалов при оценке случайных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погрешностей, т.к. доверительный интервал суммы не равен сумме доверительных интервалов. Суммируются дисперсии независимых случайных величин: D å = åDi. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностями.
Систематические погрешности Обнаружение и исключение систематических погрешностей представляет собой сложную задачу, требующую глубокого анализа всей совокупности результатов наблюдений, используемых средств, методов и условий измерений. При этом необходимо отметить, что устранение систематических погрешностей осуществляется не путем математической обработки результатов наблюдений, а применением соответствующих методов измерений. В частности, проведением измерений различными независимыми методами или выполнением измерений с параллельным применением более точных средств измерений. Существуют некоторые специальные приемы проведения измерений, которые позволяют исключить части систематических погрешностей: 1. Исключение самого источника погрешностей. 2. Замещение измеряемой величины равновеликой ей известной величиной так, чтобы при этом в состоянии и действии всех используемых средств измерений не происходило никаких изменений. Таким путем может быть исключена погрешность компаратора. 3. Компенсация погрешности по знаку путем проведения измерений в прямом и обратных направлениях одним и тем же прибором. Например, определяя значение измеряемой величины при подходе к определенной точке шкалы слева и справа от нее и вычисляя среднее значение. 4. Наблюдения через период изменения влияющей величины. Это позволяет исключить погрешности, изменяющиеся по периодическому закону. 5. Измерения одной величины несколькими независимыми методами с последующим вычислением среднего взвешенного значения измеряемой величины. 6. Измерения одной величины несколькими приборами с последующим вычислением среднего арифметического из показаний всех приборов. Систематические погрешности устраняются путем введения поправок, которые находятся разными путями и представляют собой значения абсолютных погрешностей, которые вычитаются из результата измерений. Так, инструментальные составляющие систематической погрешности находят по результатам поверки средств измерений. Поправки для учета влияющих величин вычисляют с использованием известных функций или коэффициентов влияния по результатам вспомогательных измерений этих величин. Но введение поправок не исключает полностью систематические погрешности, так как остаются, например, погрешности определения поправок. Эти неисключенные части представляют собой неисключенные остатки систематических погрешностей (НСП). Так как полностью исключить систематические погрешности невозможно, то возникает задача оценивания границ или других параметров этих погрешностей. Как правило, систематическая погрешность результата измерения оценивается по ее составляющим. Эти составляющие бывают либо известны заранее, либо могут быть определены с помощью вспомогательных данных, например, вычислены для каждой из влияющих величин. В качестве их могут выступать и погрешности определения поправок. Неисключенная систематическая погрешность характеризуется границей каждой ее составляющей.
В связи с этим возникает задача суммирования составляющих систематической погрешности. При этом составляющие должны рассматриваться как случайные величины и суммироваться методами теории вероятностей, что предполагает знание функции распределения этих составляющих. Однако, закон распределения элементарных составляющих погрешности, как правило, неизвестен. Поэтому при суммировании руководствуются следующим практическим правилом, основанном на здравом смысле и интуиции: 1. если известна оценка границ погрешности, то ее распределение следует считать равномерным; 2. если же известна оценка СКО погрешности, распределение следует считать нормальным. Применение этого правила позволяет статистически суммировать составляющие систематической погрешности. В соответствии с ним при отсутствии дополнительной информации неисключенные остатки систематической погрешности рассматриваются как случайные величины, имеющие равномерное распределение. Границы неисключенной систематической погрешности Q при числе слагаемых большим или равным 4 вычисляются по формуле:
где При числе слагаемых меньших или равных 3 значения Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.183.14 (0.022 с.) |
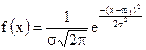
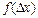 осуществляется переносом центра распределений в
осуществляется переносом центра распределений в 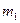 и откладывания по оси абсцисс погрешности
и откладывания по оси абсцисс погрешности 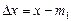 .
.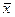 :
: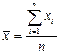 .
.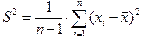
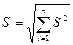 .
.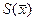 определяется по формуле:
определяется по формуле: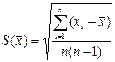
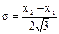 Равномерное распределение характеризуется математическим ожиданием
Равномерное распределение характеризуется математическим ожиданием 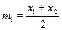 , дисперсией
, дисперсией 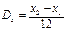 или СКО .
или СКО . 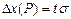
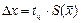
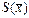 – оценка среднего квадратического отклонения среднего арифметического.
– оценка среднего квадратического отклонения среднего арифметического.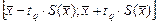 . Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.
. Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.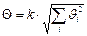
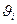 - граница i -ой составляющей погрешности; k - коэффициент, определяемый доверительной вероятностью. При Р = 0,95 k = 1.1, при Р = 0,99 k = 1,4.
- граница i -ой составляющей погрешности; k - коэффициент, определяемый доверительной вероятностью. При Р = 0,95 k = 1.1, при Р = 0,99 k = 1,4.


