
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура общего решения неоднородной линейной системы. ⇐ ПредыдущаяСтр 3 из 3
Рассмотрим неоднородную линейную систему (2.2):
Докажем следующие свойства ее решений: Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).
Доказательство. Пусть с1, с2,…,сn – решение системы (2.2), а d1, d2,…,dn – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) xi=ci+di:
После перегруппировки слагаемых получим:
Но
Свойство 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).
Доказательство. Пусть
Следствие. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).
Пример. Общее решение системы
это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых 00007081%22базисом"базисом линейного пространства. Количество векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов Правило треугольника. Для сложения двух векторов Правило параллелограмма. Для сложения двух векторов А модуль (длину) вектора суммы
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма. Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма. Сложение коллинеарных скользящих векторов Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В 02050105108105100018005100008000механике при изучении 01100108000статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы
Прямые, на которых расположены векторы Таким образом, под суммой векторов Законы умножения вектора на число. I. 1 · a = a,0 · a = 0, m · 0 = 0, (– 1) · a = – a. II. m a = a m, | m a | = | m | · | a |. III. m (n a) = (m n) a. (С о ч е т а т е л ь н ы й закон умножения на число). IV. (m + n) a = m a + n a, (Р а с п р е д е л и т е л ь н ы й m (a + b)= m a + m b. закон умножения на число).
Скалярное произведение векторов. __ __ Угол между ненулевыми векторами AB и CD – это угол, образованный векторами при их параллельном переносе до совмещения точек A и C. Скалярным произведением векторов a и b называется число, равное произведению их длин на косинус угла между ними:
Если один из векторов нулевой, то их скалярное произведение в соответствии с определением равно нулю: (a, 0) = (0, b) = 0. Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле:
Скалярное произведение (a, a), равное | a | 2, называется скалярным квадратом. Длина вектора a и его скалярный квадрат связаны соотношением:
Скалярное произведение двух векторов: - положительно, если угол между векторами острый; - отрицательно, если угол между векторами тупой. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, т.е. когда эти векторы перпендикулярны (ортогональны):
Свойства скалярного произведения. Для любых векторов a, b, c и любого числа m справедливы следующие соотношения: I. (a, b) = (b, a). (П е р е м е с т и т е л ь н ы й закон) II. (m a, b) = m (a, b). III. (a + b, c) = (a, c) + (b, c). (Р а с п р е д е л и т е л ь н ы й закон Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. Базис пространства Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов. Базисом линейного пространства называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства является линейной комбинацией этих векторов. В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует. Теорема 18.1 В линейном пространстве любые два базиса содержат одинаковое число векторов. Определение 18.3 Линейное пространство, в котором существует базис, состоящий из векторов, называется -мерным линейным или векторным пространством. Число называется размерностью пространства и обозначается. Линейное пространство, в котором не существует базис, называется бесконечномерным. Примером бесконечномерного пространства является пространство всех многочленов с вещественными коэффициентами 20) Преобразования координат при замене базиса Пусть системы векторов e = {e1,..., en} и f = {f1,..., fn} — два базиса n-мерного линейного пространства Ln. Обозначим xe = (x1,x2,..., xn) и xf = (x'1,x'2,..., x'n) — координаты вектора x ∈ Ln соответственно в базисах e и f. Справедливо следующее xe= Ce→f·xf:
Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., fn в базисе e1,..., en: f1 = с11· e2 + с21· e1 +... + сn1· en, f2 = с12· e1 + с22· e2 +... + сn2· en,..., fn = с1n· e2 +... + сnn· en. Формулу преобразования координат вектора при изменении базиса принято записывать в виде
xf= (Ce→f)− 1·xe
|
||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.79.59 (0.021 с.) |
 .
. .
. .
.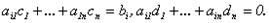 Следовательно, xi=ci+di является решением системы (2.2).
Следовательно, xi=ci+di является решением системы (2.2). и
и 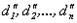 - решения системы (2.2). Тогда
- решения системы (2.2). Тогда Утверждение доказано.
Утверждение доказано.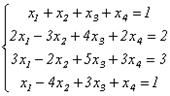 можно записать в виде:
можно записать в виде: , где
, где  - частное решение данной системы.
- частное решение данной системы. и
и  по правилу 0210510300180080треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
по правилу 0210510300180080треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. определяют по 0205010500000108011002теореме косинусов
определяют по 0205010500000108011002теореме косинусов  где
где  — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула
— угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула  теперь
теперь  и
и 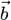 , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы  и
и  , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы 
 и
и  , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы  образуют пару (векторов).
образуют пару (векторов).







