Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие модели. Понятие моделирования. Типы моделирования.Стр 1 из 6Следующая ⇒
Понятие модели. Понятие моделирования. Типы моделирования. Требования, предъявляемые к моделям. Математическое моделирование. Классификация математических моделей. Модель – это материальный или же мысленно представляемый объект, который в процессе познания замещает объект – оригинал, при этом сохраняет некоторые важные для данного исследования типичные его черты. Модель всегда создается для конкретного исследования. Моделирование – это представление различных характеристик физ. или абстрактного объекта – оригинала с помощью другого объекта – модели, а так же выявление свойств объектов-оригиналов путем построения и исследования модели. Типы моделирования: 1. Материальное – воспроизводит динамические, геометрические и функциональные характеристики объекта: А) натуральное – производится над реальным объектом с последующей обработкой результатов экспериментов (научный эксперимент, комплексные испытания, производственный эксперимент) Б) физическое – оригинал и модель имеют одинаковую физ.природу, модель – уменьшенная или увеличенная копия оригинала, может протекать в реальном времени, в модельном времени и без учета времени. В) аналоговое – основано на аналогии, объект и модель имеют разную физ.природу, но подчиняются одинаковым законам и мат.ур-ям и описываются ими. 2. Идеальное – основано на мысленных сходствах модели и оригинала, носит теоретический х-р. А) интуитивная модель – не подлежит формализации, используется в тех областях, где процесс познания нах-ся на довольно низкой стадии. Б) знаковое – подлежит формализации, использует формулы, чертежи, схемы, графики и тд. К нему относится мат.мод-е (устанавливается соответствие данному реальному объекту некоторого мат.объекта, который мб описан на языке мат.логики, различных мат.методов и носит теор.х-р) Мат.модель – совокупность мат.объектов (числа, вектора, множества, формулы) или отношения между ними, к-е адекватно отображает свойства исследуемого объекта. Классификация: 1) По области применения – технические, экономические, биологические и др. 2) В зависимости от класса решаемых задач – дескрипторные, оптимизационные, имитационные, информационные и тд. 3) По хар-ру отображаемых св-в:
3.1 Структурные: А) топологические – отображаю только состав и взаимодействие между эл-ми, описываются таблицами, списками, графиками 3.2 Функциональные – отображают физ.и инф.процессы, для их описания исп-ся ур-я, системы ур-ний, к-е связывают между собой параметры объекта: Y=F(X,Q),где Y – выходные парам., X – внутренние парам., Q-внешнее воздействие. А) статистические (изучают установившиеся состояния объектов в опред.момент времени) и динамические (изучают переходные пр-сы в системах либо поведение системы во времени) Б) стахостические (отображают случайные пр-сы в объекте или же случайные воздействия на объект) и детерминированные (без случайных воздействий) В) дискретные (описывают процессы, к-е происходят в некоторые замкнутые моменты времени) и непрерывные (пр-сы с непрерывным протеканием времени), дискретно-непрерывные. Г) аналитические (необх.построение зависимости виде формул, к-я связывает параметры и элементы изучаемого объекта) и алгоритмические (связь между элементами и параметрами объекта выражается виде алгоритмов) 4. В зависимости от места, занимаемого в иерархии описаний – микромодели (пространство и время непрерывны), макромодели (непрерывно либо пр-во, либо время) и метамодели (агрегативный подход). Требования к моделям: 1. Универсальность 2. Точность 3. Адекватность – модель должна отображать необходимые свойства объектов в некотором заданном диапазоне и должна соответствовать изучаемым системам и технолгич.задачам. 4. Удобство работы 5. Экономичность 6. Должна поддерживаться достаточная скорость работы 7. Наглядность результата Физическое моделирование. Понятие подобия. Критерии подобия. Первая теорема подобия. Зависимые и независимые единицы измерения. Нахождение числа критериев подобия. Вторая теорема подобия. Третья теорема подобия. Пусть имеется некоторый оригинал, описываемый как некая ф-ция от некоторого набора параметров
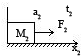
Проблема заключается в том, что не все mi могут принимать независимые значения, поскольку среди параметров X есть взаимосвязанные, например, физическими законами. Простейший случай I=U/R, тогда mi=mU/mR. Поэтому из трех величин произвольно могут быть выбраны только две. Правило выбора масштабных соотношений определяет теория подобия, в основе которой лежат три теоремы. Тогда под подобием понимают такое взаимооднозначное соответствие между параметрами модели и объекта, при котором правила перехода (критерии подобия) от X i м к X i0 известны. Первая теорема подобия (теорема Ньютона-Бертрана): подобные явления имеют определенные сочетания параметров, называемые критериями подобия (π), численно одинаковые. Проиллюстрируем примеры следующими примерами: пусть имеем механические поступательные системы, подчиняющиеся второму закону Ньютона:
Согласно второму закону Ньютона они описываются уравнениями вида:
M1=mM·M2; x1=mx·x2; t1=mt·t2 – тогда уравнения примут следующий вид:
Произвольно введем масштабные коэффициенты:
Подставляя полученные соотношения в уравнение (3), имеем:
Сравнивая (4) и (5), приходим к фундаментальному соотношению для механических поступательных систем: Переходя от масштаба к соответствующим физическим величинам, получаем формулировку критерия подобия Ньютона: Следствие: количество критериев подобия всегда на единицу меньше числа членов уравнения, описывающего исследуемый процесс. Критерий Ньютона является динамическим, поскольку в него входит время. Кроме динамических существует статистические критерии, например: для электрических цепей, подчиняющихся закону Ома, имеем:. Вторая теорема подобия: всякое полное уравнение физического процесса, записанное в определенной системе единиц измерения, может быть представлено функциональной зависимостью критериев подобия. Полным уравнением будем называть уравнение, в которое входят все интересующие нас в данном случае физические величины. Системой единиц измерения называется совокупность определенным образом установленных единиц измерения, физических величин, которая включает основные (первичные), производные (вторичные) и дополнительные единицы измерения. Основные единицы измерения выбираются произвольно! ГОСТ 8.417-81 называется «Единицы физических величин», определяет систему СИ, в которой введено семь основных единиц: - длина, L. м; масса, M, кг; время, T, с; сила электрического тока, I, А; термодинамическая температура, Θ, К; количество вещества, N, моль; сила света, J, кд. Дополнительными единицами являются радиан и стерадиан. Производные единицы измерения выражаются через основные с помощью формул размерности, которые отражают те или иные физические законы, например: из второго закона Ньютона следует формула размерности вида f=ma; [f]=[M]1[L]1[T]-2=кг·м·с-2=Н. Аналогично устанавливаются единицы измерения для электрических величин:
- потенциал, разность потенциалов, напряжение, Вольт [B]=[L]2[M]1[T]-3[I]-1; - емкость, Фарада [Ф]=[L]-2[M]-1[T]4[I]2; - сопротивление, Ом [Ом]=[L]2[M]1[T]-3[I]-2; - индуктивность, Генри [Гн]=[L]2[M]1[T]-2[I]-2. Группой независимых параметров объекта (процесса) называется такая группа, в которой размерность ни одного параметра не может быть получена из размерностей других параметров. Например, параметры m (масса), x (перемещение), υ (скорость) образуют группу независимых параметров, а группа m, f, a является группой зависимых параметров →f-ma=0. Тогда некий объект (процесс) можно описать функциональной зависимостью бита O=f(x1,x2,…,xk,xk+1,…,xm), где x1,…,xk – независимые параметры, а xk+1,…,xm – зависимые. Тогда количество критериев подобия будет равно m-k, т.е. будем иметь π1,π2,…, πm-k, а k=rankA, A – матрица, образованная в формулу размерности для параметров x1,xm. Рангом матрицы называется наибольший порядок определителя отличного от нуля. В результате Критерии определяются следующим образом: разделим параметр на группы независимых и зависимых. Независимыми являются i,R,T; зависимыми являются L,U. Тогда в конечном итоге имеем:
В результате формальная запись теоремы принимает вид: O=f(1,1,1,π1,π2). Итог: таким образом, первая теорема вводит само понятие критерия подобия как безмерной величины, связывающих физические параметры объекта или процесса. Вторая теорема дает формальную процедуру для определения количества и конкретного вида критериев подобия, используя понятие формулы размерности. Третья теорема подобия (теорема Кирпичева-Гухмана): необходимым и достаточным условиями для создания подобия являются: а) пропорциональность сходственных параметров, входящих в условия однозначности; б) равенство критериев подобия сопоставляемых явлений (процессов). Для примера рассмотрим электрическую схему из последовательно соединенных источника э.д.с. U, ключа Кл, емкости С, индуктивности L и сопротивления R (рис. 2.4). Решение систем нелинейных уравнений. Метод итерации, условие сходимости. Методы спуска. Метод покоординатного спуска. Метод градиентного спуска. Метод наискорейшего градиентного спуска. Метод Ньютона.
Первый этап: приближенные значения корней Второй этап: уточнение корней. Метод итерации:
Пускай к-либо способом мы преобразовали ур-е. начальное приближение мы подставляем в правую часть, получаем:
Строим итерационный пр-с, к-й сходится к решению в том случае, если все собственные числа |A|<1.
Более слабое условие: сумма модулей коэф-тов столбцов дБ меньше 1.
Этот ит пр-с заканчивается в том случае, когда разность между всеми неизвестными на (k+1)-шаге и на к-м шаге не будет превосходить заданного значения Погрешность решения можно оценить с пом формулы:
Методы спуска: Для всех этих методов характерно наличие ф-ции f такой, что при переходе от одной точки решения x0 к след x1 значение f уменьшится. Ф-я Ф-целевая ф-я и многие задачи по решению СНАУ сводятся к нахождению Ф.
Можно заметить, что при значениях переменных xi, явл корнями системы, Ф=0. Это происходит только в идеальном случае. Для приближенного решения надо найти min Ф(х) на области определения. Задача по решению СНАУ сводится к задаче поиска экстремума ф-ции. Таким образом, идея методов спуска в том, чтобы из начальной точки Метод покоординатного спуска: Из исходной СНАУ составляем Ф и дано 1. Фиксируем все переменные, кроме 2. Фиксируем все пер, кроме Аналогично поступая, находим Метод градиентного спуска: Градиент – это вектор, к-й имеет направление нормали к пов-ти уровня Ф(x)=const в сторону возрастания ф-ции. Нам задано приблизительно Метод наискорейшего градиентного спуска: На каждой итерации меняется значение шага h. Можно определить зн-е Ф слева и справа.
Для того, чтобы на каждой итерации h был max возможным, необходимо, чтобы на этой итерации значение Ф max уменьшалось. Метод Ньютона: Для этого метода х0 дб достаточно приближенным к решению.
Это разложение подставляем вместо исходной ф-ции
Если исходные нелинейные ур-я были относительно Системе в матричном виде относительно вектора Получаем вектор перехода к нелин системе.
За решение исх системы берем Понятие интерполяции. Виды интерполяции. Конечные и разделенные разности. Их свойства и применение. Интерполяция параболическими полиномами по методу Ньютона и методу Лагранжа. Понятие сплайн – интерполяции. Интерполяция сплайнами второго порядка.
Интерполяция – это построение достаточно простой для вычисления ф-ции f(x), совпадающей в узлах со значениями исходной ф-ции f(x), а в остальных точках отрезка [a,b] приближенно представляющая функцию с заданной точностью. Различают в зависимости от решаемых задач несколько классов интерполяции ф-ции. Дана f(x): Нужно построить 1) Параболическая интерполяция
В основе применения лежит теорема Вейерштрасса: если f(x) непрерывна на [a,b],то для любого сколь угодно малого 𝛆 существует полином В данном случае задача сводится к поиску полинома наименьшей степени k и требуемой точности совпадения. Самый простой путь поиска коэффициентов:
2) Интерполяция тригонометрическими полиномами
m-порядок полинома. 3) Интерполяция показательными полиномами
Для поиска степени искомого полинома используем конечные разности. Ф-я f(x) задана таблично, узлы - равноотстающие конечные разности 1-го порядка.
…
Конечных разностей первого порядка на 1 меньше кол-ва узлов. Конечные разности 2-го порядка:
Конечные разности k-го порядка:
Свойства конечных разностей: 1. Конечные разности константы=0 2. 3. 4. При h Разделенные разности. В том случае, когда шаг переменный, используем разделенные разности.
k-й порядок: Свойства разделенных разностей эквивалентны свойствам конечных разностей
Степень интерполяционного полинома в случае не равно отстоящих узлов выбираются таким образом, чтобы она совпадала с порядком разделенных разностей. ИП Лагранжа Пускай дана таблично заданная ф-я f(x), и мы установили, что искомый многочлен дБ степени k. Для построения полинома строится полином след.вида:
1. Степень i-го полинома влияния=k 2. I-й полином влияния в i-м узле=1. 3. I-й полином влияния во всех остальных узлах=0 В точке λ, которая не совпадает ни с одним узлом, погрешность равна: Теорема: существует единственный полином в степени k, проходящий через (k+1) точку плоскости, удовлетворяющий начальным условиям. Погрешность можно оценить следующим образом:
К достоинствам полинома Лагранжа можно отнести тот факт, что коэф-ты полинома зависят только от узлов интерполяции, но в том случае, если добавлен хотя бы 1 узел, то придется пересчитывать все полиномы. Полином Ньютона. F(x): Строится с помощью разделенных разностей.
Свойства: 1. Степень 2. В узлах полином совпадает с исходной ф-ей Положительные стороны: 1. Не требуется вычислять степень полинома. Можно взять 2-ю степень, построить, проверить погрешность, если не удовлетворяет, то повышаем степень до необх точности. 2. При добавлении новой k+1 точки, все найденные ранее коэф-ты сохраняются, а к полиному добавляется:
Сплайн-интерполяция. f(x) задана на Сплайн порядка n – функция, определенная на Пусть ф-я Sn на Параболическая сплайн-интерполяция Пусь f(x) задана таблично, S2(x)=S2i(x)= На каждом Для построения такого сплайна необходимо найти 3n коэф-та, все они находятся из след условий: 1. Совпадение сплайна на каждом отрезке с заданной ф-ей
2. Непрерывность первой производной в узлах. Равенство производных соседних полиномов в узле – условие для внутренних узлов. 3. Мы можем задать значение 1-й производной в x0 либо в xn. Этих условий достаточно, для определение единственного сплайна S2 на отрезке. Погрешность оценивается след образом:
Решение обыкновенных дифференциальных уравнений. Методы решения. Задача Коши. Краевая задача. Решение ОДУ методом Эйлера, модифицированным методом Эйлера, методом Рунге – Кутта, методами прогноза и коррекции. Решение ОДУ большого порядка. Решение систем ОДУ. Методы решения краевых задач. Ур-ния, содержащие неизвестную ф-цию под знаком производной, называются дифференциальными уравнениями. Если ур-ние содержит одну независимую переменную и производную по ней, то оно называется обыкновенным, т.е. ОДУ. Решить ОДУ – это значит найти некоторую ф-цию, которая удовлетворяла бы как самому ур-нию, так, возможно, дополнительным условиям. В зависимости от дополнительных условий различают задачу Коши и краевую задачу. Для решения задачи Коши существует набор хорошо апробированных методов, а решение каждой отдельной краевой задачи может потребовать специфических подходов. Поэтому в классической вычислительной математике рассматривают вычисления задачи Коши, которую в простейшем случае можно рассмотреть следующим образом: Задано ОДУ первого порядка: Решение: 1).x1=x0+h; 2)tgα=f(x0,y0); 3)y=y0=tgα(x-x0); 4)x=x1, y=y1; 5)x1y1 Численные методы для решения этой задачи могут быть разбиты на две группы: одношаговые и многошаговые. Одношаговый метод. В основе всех одношаговых методов лежит разложение ф-ций в ряд Тейлора:
y(x+h)=y(x)+hy’(x)+O(h2)
В результате имеем общую формулу метода Эйлера: Несомненное преимущество метода Эйлера – простота реализации. Существенный недостаток – крайне низка точность, которую, однако, можно заранее оценить.(с каждым шагом глобальная погрешность увеличивается) Как правило, для повышения точности осуществляют решение с шагом h, с шагом h/2 и т.д. В этом случае процедуру называют самоконтролирующей или с автоматическим выбором шага. Все остальные одношаговые методы базируются на идее Эйлера, но для значительного повышения точности используются дополнительные точки. Модифицированный метод Эйлера:
3)tg α1=f(x1,y1) 4) tg αср= (tg α0- tg α1)/2 5)y=y0+ tg αср(x-x0) 6)x=x1 след. y1ср; 7)x1,y1ср Точка по модиф. мет. Эйлера гораздо ближе к искомой, чем точка по обычному мет. Эйлера. Классическим считается метод Рунге-Кутта четвертого порядка точности. yn+1=yn+1/6(k0+2k1+2k2+k3) k0=hf(xn;yn) k1=hf(xn+1/2h;yn+1/2k0) k2=hf(xn+1/2h;yn+1/2k1) k3=hf(xn+1/2h;yn+k2) δ= |yn(h)-yn(h/2)|/15 Ошибка пропорциональна O(h5). Этот метод сочетает простоту реализации с достаточной
Нелинейное программирование (НП). Аналитические условия решения задач НП. Типы методов НП. Методы решения задач одномерной минимизации. Метод дихотомии. Метод золотого сечения. Методы решения задач многомерной оптимизации. Метод случайного поиска. Метод деформируемого многогранника Нелдера-Мида. Нелинейное программирование — раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями. В краткой форме задачу н. п. можно записать так: F (x) → max при условиях g (x) ≤ b, x ≥ 0, где x — вектор искомых переменных; F (x) — целевая функция; g (x) — функция ограничений (непрерывно дифференцируемая); b — вектор констант ограничений (выбор знака ≤ в первом условии здесь произволен, его всегда можно изменить на обратный). Решение задачи НП (глобальный макс или мин) может принадл либо границе, либо внутренней части допустимого множества. Задача состоит в выборе таких неотрицательных значений переменных, подчиненных системе ограничений в форме неравенств, при к-х достигается макс (или мин) данной ф-и. При этом не оговариваются формы ни целевой функции, ни неравенств. Могут быть разные случаи: целевая функция нелинейна, а ограничения линейны; целевая функция линейна, а ограничения (хотя бы одно из них) нелинейны; и целевая функция, и ограничения нелинейны. Задачи, в к-х число переменных и (или) число ограничений бесконечно, называются задачами бесконечномерного н. п. Задачи, в которых целевая ф-я и (или) ф-и ограничений содержат случайные элементы, называются задачами стохастического н. п. Метод дихотомии. На каждом шаге итерационного процесса использ следующие соотношения: x1(n) = (an+bn)/2- Возможны след варианты: - f(x1(n))>f(x2(n)) -> an+1= x1(n) ; bn+1=bn - f(x1(n))< f(x2(n)) -> an+1= an ; bn+1=x2(n) - f(x1(n))= f(x2(n)) -> an+1= x1(n) ; bn+1= x2(n)
Метод золотого сечения. Более эффективный метод, и самый распространенный.Считается, что отрезок поделен по методу золотого сечения, если: l2 / l = l1 / l2; если l=1, то l1= 0.382, l2=0.618. Общая процедура метода сводится к след формулам: x1(n) =an+0.382(bn-an) x2(n) =bn-0.382(bn-an) Возможны след варианты: - f(x1(n))>f(x2(n)) -> an+1= x1(n) ; bn+1=bn - f(x1(n))< f(x2(n)) -> an+1= an ; bn+1=x2(n) - f(x1(n))= f(x2(n)) -> an+1= x1(n) ; bn+1= x2(n)
Понятие модели. Понятие моделирования. Типы моделирования. Требования, предъявляемые к моделям. Математическое моделирование. Классификация математических моделей. Модель – это материальный или же мысленно представляемый объект, который в процессе познания замещает объект – оригинал, при этом сохраняет некоторые важные для данного исследования типичные его черты. Модель всегда создается для конкретного исследования. Моделирование – это представление различных характеристик физ. или абстрактного объекта – оригинала с помощью другого объекта – модели, а так же выявление свойств объектов-оригиналов путем построения и исследования модели. Типы моделирования: 1. Материальное – воспроизводит динамические, геометрические и функциональные характеристики объекта: А) натуральное – производится над реальным объектом с последующей обработкой результатов экспериментов (научный эксперимент, комплексные испытания, производственный эксперимент) Б) физическое – оригинал и модель имеют одинаковую физ.природу, модель – уменьшенная или увеличенная копия оригинала, может протекать в реальном времени, в модельном времени и без учета времени. В) аналоговое – основано на аналогии, объект и модель имеют разную физ.природу, но подчиняются одинаковым законам и мат.ур-ям и описываются ими. 2. Идеальное – основано на мысленных сходствах модели и оригинала, носит теоретический х-р. А) интуитивная модель – не подлежит формализации, используется в тех областях, где процесс познания нах-ся на довольно низкой стадии. Б) знаковое – подлежит формализации, использует формулы, чертежи, схемы, графики и тд. К нему относится мат.мод-е (устанавливается соответствие данному реальному объекту некоторого мат.объекта, который мб описан на языке мат.логики, различных мат.методов и носит теор.х-р) Мат.модель – совокупность мат.объектов (числа, вектора, множества, формулы) или отношения между ними, к-е адекватно отображает свойства исследуемого объекта. Классификация: 1) По области применения – технические, экономические, биологические и др. 2) В зависимости от класса решаемых задач – дескрипторные, оптимизационные, имитационные, информационные и тд. 3) По хар-ру отображаемых св-в: 3.1 Структурные: А) топологические – отображаю только состав и взаимодействие между эл-ми, описываются таблицами, списками, графиками 3.2 Функциональные – отображают физ.и инф.процессы, для их описания исп-ся ур-я, системы ур-ний, к-е связывают между собой параметры объекта: Y=F(X,Q),где Y – выходные парам., X – внутренние парам., Q-внешнее воздействие. А) статистические (изучают установившиеся состояния объектов в опред.момент времени) и динамические (изучают переходные пр-сы в системах либо поведение системы во времени) Б) стахостические (отображают случайные пр-сы в объекте или же случайные воздействия на объект) и детерминированные (без случайных воздействий) В) дискретные (описывают процессы, к-е происходят в некоторые замкнутые моменты времени) и непрерывные (пр-сы с непрерывным протеканием времени), дискретно-непрерывные. Г) аналитические (необх.построение зависимости виде формул, к-я связывает параметры и элементы изучаемого объекта) и алгоритмические (связь между элементами и параметрами объекта выражается виде алгоритмов) 4. В зависимости от места, занимаемого в иерархии описаний – микромодели (пространство и время непрерывны), макромодели (непрерывно либо пр-во, либо время) и метамодели (агрегативный подход). Требования к моделям: 1. Универсальность 2. Точность 3. Адекватность – модель должна отображать необходимые свойства объектов в некотором заданном диапазоне и должна соответствовать изучаемым системам и технолгич.задачам. 4. Удобство работы 5. Экономичность 6. Должна поддерживаться достаточная скорость работы 7. Наглядность результата Физическое моделирование. Понятие подобия. Критерии подобия. Первая теорема подобия. Зависимые и независимые единицы измерения. Нахождение числа критериев подобия. Вторая теорема подобия. Третья теорема подобия.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 1368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.15.1 (0.204 с.) |
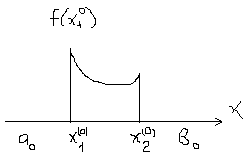
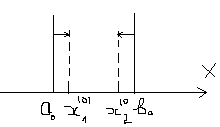
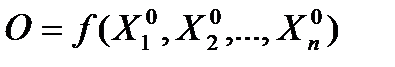 , и модель, описываемая как
, и модель, описываемая как 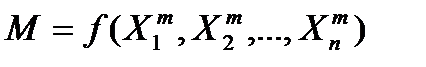 . Если для всех параметров xi выполняются соотношения,
. Если для всех параметров xi выполняются соотношения, 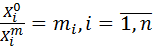 , то говорят, что объект и модель подобны. Это означает, что, исследуя свойства модели, можно перенести полученные результаты на объект, пересчитав все параметры с помощью масштабов mi.
, то говорят, что объект и модель подобны. Это означает, что, исследуя свойства модели, можно перенести полученные результаты на объект, пересчитав все параметры с помощью масштабов mi.
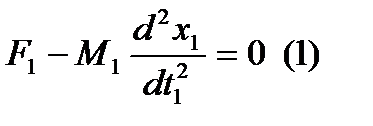

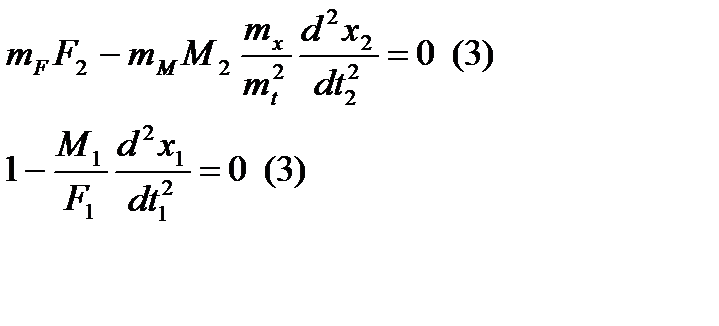
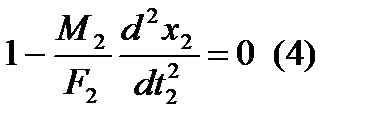
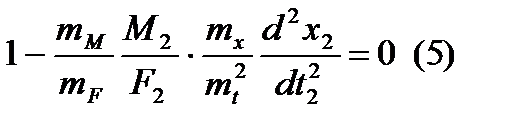
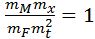
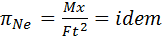 . Оно справедливо для всех подобных механических поступательных систем.
. Оно справедливо для всех подобных механических поступательных систем.
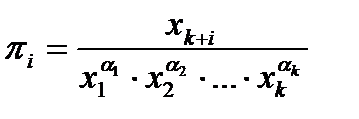 , где αi – целочисленная степень.
, где αi – целочисленная степень.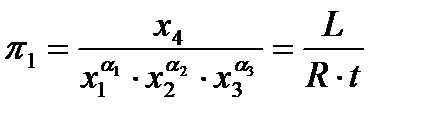
 . Причем
. Причем 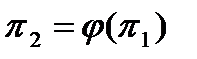 ,
, 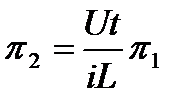
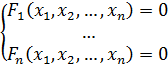 F(
F( )=0
)=0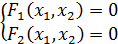 => >
=> > 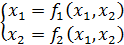
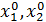
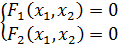 начальные значения корня (
начальные значения корня (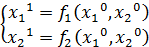 =>
=> 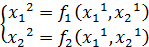 =>
=> 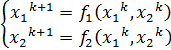

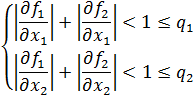
 и за решение можно взять решение, найденное на к+1 шаге.
и за решение можно взять решение, найденное на к+1 шаге.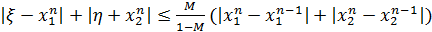 , M=max(
, M=max(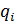 )
)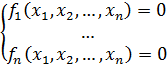

 перейти в
перейти в  таким образом, чтобы зн-я Ф уменьшилось. Этот итерационный пр-с можно повторять, но на каждом шаге зн-е Ф д уменьшаться. Этот ит пр-с заканчивается, когда
таким образом, чтобы зн-я Ф уменьшилось. Этот итерационный пр-с можно повторять, но на каждом шаге зн-е Ф д уменьшаться. Этот ит пр-с заканчивается, когда 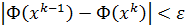 . За решение можно взять вектор
. За решение можно взять вектор 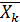 .
.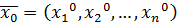
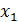 , и находим min Ф на ООФ по переменной
, и находим min Ф на ООФ по переменной 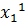 : Ф
: Ф 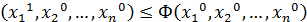 . Значение Ф(
. Значение Ф(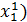 уменьшилось, тк искали min Ф по координате
уменьшилось, тк искали min Ф по координате  , находим min
, находим min 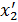 , так делаем n шагов. Перейдем от
, так делаем n шагов. Перейдем от 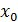 к
к  и значение Ф в
и значение Ф в  . Ф(
. Ф(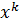 )
) 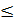 Ф(
Ф(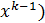 , делаем так, пока
, делаем так, пока 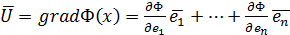
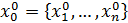 , выбираем шаг h>0. Строим ит пр-с:
, выбираем шаг h>0. Строим ит пр-с: 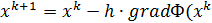 ). Поскольку стоит минус, то будем переходить в сторону убывания ф-ции, на каждом шаге зна-е Ф уменьшается. Так до тех пор, пока
). Поскольку стоит минус, то будем переходить в сторону убывания ф-ции, на каждом шаге зна-е Ф уменьшается. Так до тех пор, пока 
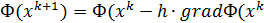 ))
)) )).На каждой итерации получается свое значение шага.
)).На каждой итерации получается свое значение шага.

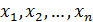 , то преобразованную систему мы получили относительно
, то преобразованную систему мы получили относительно 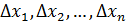 .
.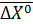 :
: 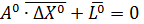 - линейная система.
- линейная система.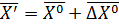 - начальная точка для следующей итерации.
- начальная точка для следующей итерации.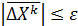
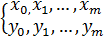
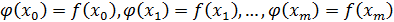
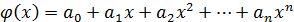
 , такой что для любого х
, такой что для любого х 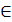 [a,b]:
[a,b]: 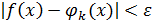
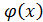 ищем в виде полинома. Для каждой заданной точки составляем равенство искомого полинома и значения ф-ции в узле. Получаем СЛАУ, при этом степень полинома должна соответствовать кол-ву уравнений +1.
ищем в виде полинома. Для каждой заданной точки составляем равенство искомого полинома и значения ф-ции в узле. Получаем СЛАУ, при этом степень полинома должна соответствовать кол-ву уравнений +1.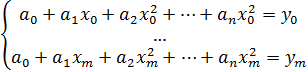
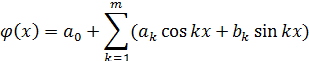

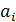 - постоянная времени
- постоянная времени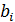 - придаточный коэф-т
- придаточный коэф-т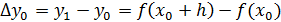
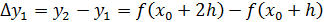
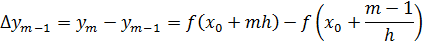

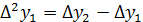

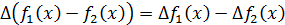
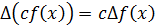
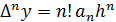
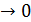 конечные разности первого порядка соответствуют
конечные разности первого порядка соответствуют 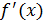 ,
, 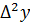 =
= 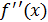 и т.д.
и т.д.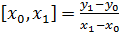
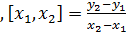 ,
, 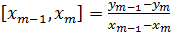 - первый порядок
- первый порядок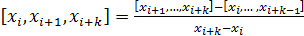

 , где
, где 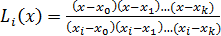 - многочлен Лагранжа
- многочлен Лагранжа . Если искомая ф-я f(x)-полином, тогда погрешность=0.
. Если искомая ф-я f(x)-полином, тогда погрешность=0.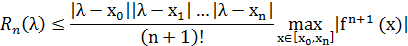
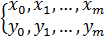
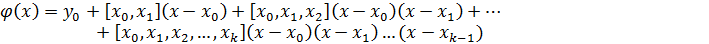
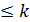
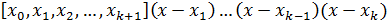
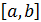 таблично, весь отрезок разбит точками
таблично, весь отрезок разбит точками  .
.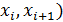 задана полиномом Sni=
задана полиномом Sni= 
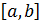 имеет k непрерывных
имеет k непрерывных 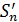 , тогда d=n-k – дефект сплайна.
, тогда d=n-k – дефект сплайна.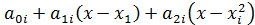

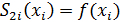
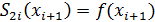
 , h=max
, h=max 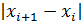
 и начальное условие: y(x0)=y0. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию.
и начальное условие: y(x0)=y0. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию. , в котором сохраняются члены до установленного порядка. Если сохраняется член вида
, в котором сохраняются члены до установленного порядка. Если сохраняется член вида  , то говорят, что метод имеет порядок n, а погрешность метода пропорциональна hn+1. Для нахождения следующей точки y(xk+1) требуется информация только об одной предыдущей точке y(xk) – способность самостартования.
, то говорят, что метод имеет порядок n, а погрешность метода пропорциональна hn+1. Для нахождения следующей точки y(xk+1) требуется информация только об одной предыдущей точке y(xk) – способность самостартования. Простейшим представителем одношаговых методов является метод Эйлера.
Простейшим представителем одношаговых методов является метод Эйлера.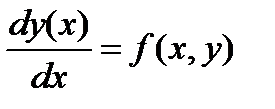
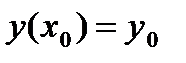


 y(x0)=y0, k=0,1,2,…
y(x0)=y0, k=0,1,2,…
 /2 x2(n) = (an+bn)/2+
/2 x2(n) = (an+bn)/2+  /2
/2