
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцируемость Г- функций
Г-функция бесконечное число раз дифференцируема, производные могут быть найдены внесением дифференцирования под знак интеграла.
Функция-оригинал ~ Преобразование Лапласа ~ Основные свойства преобразования Лапласа
Операционное исчисление - один из наиболее эффективных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. При решении операционным методом задача интегрирования линейного дифференциального уравнения с постоянными коэффициентами Функцией-оригиналом называется функция f (x) для которой справедливо: Преобразованием Лапласа функции f (x) называется функция Функция F (p) называется изображением функции f (x), а функция f (x) - оригиналом для F (p).
ПРИМЕР 1. Отыскание изображения и оригинала.
Основные свойства преобразования Лаплалса, используемые при решении дифференциальных уравнений следующие: · оригинал восстанавливется по изображению единственным образом, с точностью до значений в точках разрыва - теорема единственности; · если F (p) и G (p) - изображения соответственно для f (x) и g (x), то изображением для af (x) + bg (x) является aF (p) + bG (p) - линейность преобразования Лапласа; · изображением для производной f (n)(x) является функция pnF (p) - pn -1 f (0) - pn -2 f '(0) -...- pf (n -2)(0) - f (n -1)(0) - изображение производных; · если F (p) изображения для f (x), то для любого a >0 изображением для f (x-a) является Теорема запаздывания. Если f (t)
Теорема. (Признак сходимости Даламбера). Пусть при всех Доказательство. Из условий теоремы следует Если В предельной форме этот признак выглядит так:
Теорема. Если существует Доказательство. При Теорема. (Признак сходимости Коши). Пусть Доказательство. Неравенство Если же В предельной форме эта теорема выглядит так: Теорема. Пусть существует Доказательство. Пусть Если же
Интегральный признак сходимости. Сходимость ряда Теорема. Пусть Доказательство. Ввиду монотонности при всех Пусть теперь наоборот, известно, что ряд сходится. Тогда
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.36.141 (0.016 с.) |


 сводится к задаче о решении алгебраического уравнения.
сводится к задаче о решении алгебраического уравнения. при всех неотрицательных x.
при всех неотрицательных x.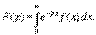
 - теорема запаздывания.
- теорема запаздывания. F (p) (т.е. f (t) · η (t)
F (p) (т.е. f (t) · η (t)  F (p)), то f (t − t 0) · η (t − t 0)
F (p)), то f (t − t 0) · η (t − t 0) 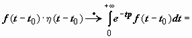


 .
. 
 , где
, где  . Тогда ряд сходится. Если же при
. Тогда ряд сходится. Если же при 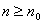
 , то ряд расходится.
, то ряд расходится.
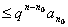 . Иными словами,
. Иными словами,  и по первой теореме сравнения ряд сходится.
и по первой теореме сравнения ряд сходится. при
при  и ряд расходится.
и ряд расходится. , то при
, то при 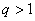 - расходится, а при
- расходится, а при  признак неприменим.
признак неприменим. так, чтобы
так, чтобы 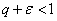 . Пусть
. Пусть 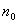 выбрано так, чтобы при
выбрано так, чтобы при  , т.е.
, т.е. 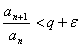 и
и  ,
, 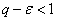 . Тогда при
. Тогда при  и ряд расходится.
и ряд расходится. и при достаточно больших
и при достаточно больших 
 . Тогда ряд
. Тогда ряд 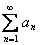 сходится. Если же при
сходится. Если же при  , то он расходится.
, то он расходится.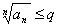 при
при 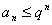 . Так как
. Так как  , ряд
, ряд  – сходится. По теореме 1 из предыдущего параграфа ряд
– сходится. По теореме 1 из предыдущего параграфа ряд 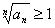 , то и
, то и  и равенство
и равенство  невозможно. Т.о. необходимый признак сходимости не выполняется и ряд расходится.
невозможно. Т.о. необходимый признак сходимости не выполняется и ряд расходится. . Тогда если
. Тогда если  ). Тогда при
). Тогда при 
 , т.е.
, т.е.  . Применяя предыдущую теорему получаем, что ряд сходится.
. Применяя предыдущую теорему получаем, что ряд сходится. (т.е.
(т.е.  ). Тогда
). Тогда 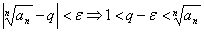 . Вновь по предыдущей теореме ряд расходится.
. Вновь по предыдущей теореме ряд расходится.
 - непрерывная, неотрицательная, монотонно убывающая функция, определенная при
- непрерывная, неотрицательная, монотонно убывающая функция, определенная при  . Тогда ряд
. Тогда ряд  и интеграл
и интеграл  либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся. . Интегрируя, получаем
. Интегрируя, получаем  . Тогда
. Тогда  , или
, или  . Поэтому если
. Поэтому если  . Тогда
. Тогда 
 и
и  ,
,  ряд сходится.
ряд сходится. . Взяв произвольное
. Взяв произвольное  выберем
выберем  . Тогда
. Тогда  . Значит,
. Значит, 


