
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод найменших квадратів (НК) з використанням MathcadСтр 1 из 2Следующая ⇒
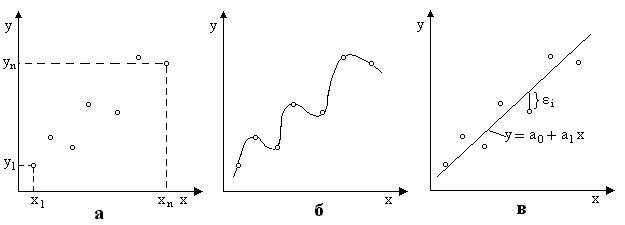
Лекція 8 Метод найменших квадратів Лінійне рівняння Коли експериментальні дані мають невелику точність, використати методи інтерполяції для їх опису досить важко, а то і неможливо. Наприклад, на рис. 8.1а зображено ряд точок які відображають залежність між y і x. Через ці точки можна провести криву, що є інтерполяційним поліномом з багатьма членами (рис. 8.1б), але її не можна буде використати для інтерполяції, бо вона дасть велику похибку. Через ці точки можна провести іншу лінію - пряму, яка в повній мірі відображує залежність між y і x. Як провести цю лінію буде залежати від того якими критеріями буде користуватися дослідник для зменшення відстані між експериментальними даними і кривою.
Один із методів знаходження коефіцієнтів рівнянь регресії, які описують експериментальні точки, називається методом найменших квадратів. Нехай експериментальні дані представлені в таблиці:
Взаємозв’язок або регресію між змінними х і у можна описати лінійною залежністю у випадку, коли коефіцієнт кореляції між параметрами х і у по модулю близький до одиниці: y = a0 + a1 x. (8.1) Так як пряма не накладається точно на точки, то при знаходженні i -го значення за формулою a0 + ai xi в порівнянні з табличним значенням yi буде виникати похибка. yi – a0 – a1xi = ei. (8.2) Задача знаходження коефіцієнтів рівняння полягає в тому, щоб сумарна похибка для всіх n точок була мінімальною:
Але цей критерій при розрахунку коефіцієнтів рівняння не може бути використаним, бо є додатні і від’ємні значення похибок. І коли сума eі буде в наведеному вище рівнянні дорівнювати 0, то це не означатиме, що похибок немає і рівняння вибране найкраще (див. рис. 8.2а).Інший варіант критерію - це вибрати мінімум суми модулів похибок:
В цьому випадку люба лінія (рис. 8.2б), що проходить симетрично поміж точками буде мати мінімальну сумарну похибку. Враховуючи це, у якості критерію оцінки рівняння вибрано мінімум суми квадратів похибок.
Використаємо цей критерій для пошуку коефіцієнтів лінійної залежності. Представимо вибраний критерій у вигляді функції
Спростивши цю систему рівнянь отримаємо:
Позначимо в цій системі рівнянь суми невідомими: åхі – S1, åxi2 – S2, åyі – S3, å(xi ×yi) – S4 і утворену систему рівнянь вирішимо методом виключення невідомих – методом Гаусса, спростивши систему з двох рівнянь до одного. Для цього помножимо перше рівняння на S1 і поділимо на n. Після цього віднімемо від першого рівняння друге.
В результаті отримаємо значення коефіцієнтів рівняння:
Для оцінки рівняння використовується середньоквадратична похибка рівняння відносно табличних даних:
де n – 1 – ступінь волі рівняння, яке має шукані два коефіцієнти. Приклад 8.1 Знайдемо коефіцієнти лінійного рівняння y = a0 + a1 x для табличних даних із шести точок, n = 6 Таблиця 8.1.
Отримаємо систему рівнянь
Розв’язавши цю систему отримаємо:
Шукане рівняння матиме вигляд:
Лінійна залежність має найпростішу методику визначення її коефіцієнтів, але це не означає, що завжди між двома змінними ця залежність лінійна. Дуже часто навіть на око можна визначити що залежність нелінійна. Як ми бачили на малюнку 4, що парабола з меншою похибкою відображає дані. Існує дуже багато нелінійних рівнянь, які можна використати для опису даних, для знаходження коефіцієнтів.
Лекція 8 Метод найменших квадратів Лінійне рівняння Коли експериментальні дані мають невелику точність, використати методи інтерполяції для їх опису досить важко, а то і неможливо. Наприклад, на рис. 8.1а зображено ряд точок які відображають залежність між y і x. Через ці точки можна провести криву, що є інтерполяційним поліномом з багатьма членами (рис. 8.1б), але її не можна буде використати для інтерполяції, бо вона дасть велику похибку. Через ці точки можна провести іншу лінію - пряму, яка в повній мірі відображує залежність між y і x. Як провести цю лінію буде залежати від того якими критеріями буде користуватися дослідник для зменшення відстані між експериментальними даними і кривою.
Один із методів знаходження коефіцієнтів рівнянь регресії, які описують експериментальні точки, називається методом найменших квадратів. Нехай експериментальні дані представлені в таблиці:
Взаємозв’язок або регресію між змінними х і у можна описати лінійною залежністю у випадку, коли коефіцієнт кореляції між параметрами х і у по модулю близький до одиниці: y = a0 + a1 x. (8.1) Так як пряма не накладається точно на точки, то при знаходженні i -го значення за формулою a0 + ai xi в порівнянні з табличним значенням yi буде виникати похибка. yi – a0 – a1xi = ei. (8.2) Задача знаходження коефіцієнтів рівняння полягає в тому, щоб сумарна похибка для всіх n точок була мінімальною:
Але цей критерій при розрахунку коефіцієнтів рівняння не може бути використаним, бо є додатні і від’ємні значення похибок. І коли сума eі буде в наведеному вище рівнянні дорівнювати 0, то це не означатиме, що похибок немає і рівняння вибране найкраще (див. рис. 8.2а).Інший варіант критерію - це вибрати мінімум суми модулів похибок:
В цьому випадку люба лінія (рис. 8.2б), що проходить симетрично поміж точками буде мати мінімальну сумарну похибку. Враховуючи це, у якості критерію оцінки рівняння вибрано мінімум суми квадратів похибок.
Використаємо цей критерій для пошуку коефіцієнтів лінійної залежності. Представимо вибраний критерій у вигляді функції
Спростивши цю систему рівнянь отримаємо:
Позначимо в цій системі рівнянь суми невідомими: åхі – S1, åxi2 – S2, åyі – S3, å(xi ×yi) – S4 і утворену систему рівнянь вирішимо методом виключення невідомих – методом Гаусса, спростивши систему з двох рівнянь до одного. Для цього помножимо перше рівняння на S1 і поділимо на n. Після цього віднімемо від першого рівняння друге.
В результаті отримаємо значення коефіцієнтів рівняння:
Для оцінки рівняння використовується середньоквадратична похибка рівняння відносно табличних даних:
де n – 1 – ступінь волі рівняння, яке має шукані два коефіцієнти. Приклад 8.1 Знайдемо коефіцієнти лінійного рівняння y = a0 + a1 x для табличних даних із шести точок, n = 6 Таблиця 8.1.
Отримаємо систему рівнянь
Розв’язавши цю систему отримаємо:
Шукане рівняння матиме вигляд:
Лінійна залежність має найпростішу методику визначення її коефіцієнтів, але це не означає, що завжди між двома змінними ця залежність лінійна. Дуже часто навіть на око можна визначити що залежність нелінійна. Як ми бачили на малюнку 4, що парабола з меншою похибкою відображає дані. Існує дуже багато нелінійних рівнянь, які можна використати для опису даних, для знаходження коефіцієнтів.
Метод найменших квадратів (НК) з використанням Mathcad
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.6 (0.022 с.) |
 . (8.3)
. (8.3) . (8.4)
. (8.4) (8.5)
(8.5)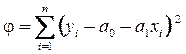 , де а0 і а1 - невідомі. Тоді, якщо функція j мінімальна, то частинні похідні по її невідомих дорівнюють нулю. Запишемо це показавши суму у спрощеному виді:
, де а0 і а1 - невідомі. Тоді, якщо функція j мінімальна, то частинні похідні по її невідомих дорівнюють нулю. Запишемо це показавши суму у спрощеному виді: (8.6)
(8.6) . (8.7)
. (8.7) (8.8)
(8.8) (8.9)
(8.9) , (8.10)
, (8.10)






