
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервалы прогноза по линейному уравнению регрессии
Прогнозирование по уравнению регрессии представляет собой подстановку в уравнение регрессии соответственного значения х. Такой прогноз
Преобразуем уравнение регрессии:
ошибка Из теории выборки известно, что Используем в качестве оценки s2 остаточную дисперсию на одну степень свободы S2, получаем: Ошибка коэффициента регрессии из формулы (15):
Таким образом, при х=хk получаем:
Как видно из формулы, величина
Для нашего примера эта величина составит:
При
Для прогнозируемого значения
т.е. при хk =4 уp =-5,79+36,84·4=141,57 - это точечный прогноз. Прогноз линии регрессии лежит в интервале: 132,99 ≤ Мы рассмотрели доверительные интервалы для среднего значения у при заданном х. Однако фактические значения у варьируются около среднего значения
Для примера:
Доверительный интервал прогноза индивидуальных значений у при хк =4 с верностью 0,95 составит:. 141,57 ±2,57·8,01, или 120,98 ≤ ур ≤ 162,16. Пусть в примере с функцией издержек выдвигается предположение, что в предстоящем году в связи со стабилизацией экономики затраты на производство 8 тыс. ед. продукции не превысят 250 млн. руб. Означает ли это изменение найденной закономерности или затраты соответствуют регрессионной модели? Точечный прогноз:
Сравним ее с предполагаемым снижением издержек производства, т.е. 250-288,93= -38,93:
Поскольку оценивается только значимость уменьшения затрат, то используется односторонний t~ критерий Стьюдента. При ошибке в 5 % с n-2=5 tтабл =2,015, поэтому предполагаемое уменьшение затрат значимо отличается от прогнозируемого значения при 95 % - ном уровне доверия. Однако, если увеличить вероятность до 99%, при ошибке 1 % фактическое значение t -критерия оказывается ниже табличного 3,365, и различие в затратах статистически не значимо, т.е. затраты соответствуют предложенной регрессионной модели.
Нелинейная регрессия До сих пор мы рассматривали лишь линейную модель регрессионной зависимости у от х (3). В то же время многие важные связи в экономике являются нелинейными. Примерами такого рода регрессионных моделей являются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства - трудом, капиталом и т.п.) и функции спроса (зависимости между спросом на какой-либо вид товаров или услуг, с одной стороны, и доходом и ценами на этот и другие товары - с другой). При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации. В случае линеаризации нелинейной зависимости получаем линейное регрессионное уравнение типа (3), параметры которого оцениваются обычным МНК, после чего можно записать исходное нелинейное соотношение. Несколько особняком в этом смысле стоит полиномиальная модель произвольной степени:
к которой обычный МНК можно применять без всякой предварительной линеаризации. Рассмотрим указанную процедуру применительно к параболе второй степени:
Такая зависимость целесообразна в случае, если для некоторого интервала значений фактора возрастающая зависимость меняется на убывающую или наоборот. В этом случае можно определить значение фактора, при котором достигается максимальное или минимальное значение результативного признака. Если исходные данные не обнаруживают изменение направленности связи, параметры параболы становятся трудно интерпретируемыми, и форму связи лучше заменить другими нелинейными моделями. Применение МНК для оценки параметров параболы второй степени сводится к дифференцированию суммы квадратов остатков регрессии по каждому из оцениваемых параметров и приравниванию полученных выражений нулю. Получается система нормальных уравнений, число которых равно числу оцениваемых параметров, т.е. трем:
Решать эту систему можно любым способом, в частности, методом определителей. Экстремальное значение функции наблюдается при значении фактора, равном:
Если b>0, с<0, имеет место максимум, т.е. зависимость сначала растет, а затем падает. Такого рода зависимости наблюдаются в экономике труда при изучении заработной платы работников физического труда, когда в роли фактора выступает возраст. При b<0, с>0 парабола имеет минимум, что обычно проявляется в удельных затратах на производство в зависимости от объема выпускаемой продукции. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей. Зависимости гиперболического типа имеют вид:
Примером такой зависимости является кривая Филлипса, констатирующая обратную зависимость процента прироста заработной платы от уровня безработицы. В этом случае значение параметра b будет больше нуля. Другим примером зависимости (37) являются кривые Энгеля, формулирующие следующую закономерность: с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается, а доля доходов, расходуемых на непродовольственные товары, будет возрастать. В этом случае b <0, а результативный признак в (37) показывает долю расходов на непродовольственные товары. Линеаризация уравнения (37) сводится к замене фактора z=1/х, и уравнение регрессии имеет вид (3), в котором вместо фактора х используем фактор z:
К такому же линейному уравнению сводится полулогарифмическая кривая:
которая может быть использована для описания кривых Энгеля. Здесь 1п(х) заменяется на z, и получается уравнение (38). Достаточно широкий класс экономических показателей характеризуется приблизительно постоянным темпом относительного прироста во времени. Этому соответствуют зависимости показательного (экспоненциального) типа, которые записываются в виде:
или в виде
Возможна такая зависимость:
В регрессиях типа (40) - (42) применяется один и тот же способ линеаризации - логарифмирование. Уравнение (40) приводится к виду:
Замена переменной Y = ln у сводит его к линейному виду:
где
который отличается от (43) только видом свободного члена, и линейное уравнение выглядит так: Y=A+bx+E (46) где A= ln a. Параметры А и b получаются обычным МНК, затем параметр а в зависимости (41) получается как антилогарифм А. При логарифмировании (42) получаем линейную зависимость: Y=A+Bx+E (47) где B =ln b, а остальные обозначения те же, что и выше. Здесь также применяется МНК к преобразованным данным, а параметр b для (42) получается как антилогарифм коэффициента В. Широко распространены в практике социально-экономических исследований степенные зависимости. Они используются для построения и анализа производственных функций. В функциях вида:
особенно ценным является то обстоятельство, что параметр b равен коэффициенту эластичности результативного признака по фактору х. Преобразуя (48) путем логарифмирования, получаем линейную регрессию: Y=A+bX+E (49) где Y= ln y, A= ln a, X= ln x, E= ln ε. Еще одним видом нелинейности, приводимым к линейному виду, является обратная зависимость:
Проводя замену и = 1/у, получим:
Наконец, следует отметить зависимость логистического типа:
Графиком функции (52) является так называемая «кривая насыщения», которая имеет две горизонтальные асимптоты у=0 и у=1/а и точку перегиба x= ln (b/a), у=1/(2а), а также точку пересечения с осью ординат у=1/(а+b):
Уравнение (52) приводится к линейному виду заменами переменных и=1/у, z=e-x. Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:
Здесь
Величина R находится в границах 0 ≤ R ≤ 1, и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с линейным коэффициентом корреляции в случае, когда преобразование переменных с целью линеаризации уравнения регрессии не проводится с величинами результативного признака. Так обстоит дело с полулогарифмической и полиномиальной регрессией, а также с равносторонней гиперболой (37). Определив линейный коэффициент корреляции для линеаризованных уравнений, например, н пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и для нелинейной зависимости. Иначе обстоит дело в случае, когда преобразование проводится также с величиной у, например, взятие обратной величины или логарифмирование. Тогда значение R, вычисленное той же функцией ЛИНЕЙН, будет относиться к линеаризованному уравнению регрессии, а не к исходному нелинейному уравнению, и величины разностей под суммами в (54) будут относиться к преобразованным величинам, а не к исходным, что не одно и то же. При этом, как было сказано выше, для расчета R следует воспользоваться выражением (54), вычисленным по исходному нелинейному уравнению.
Поскольку в расчете индекса корреляции используется соотношение факторной и общей СКО, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации. Оценка существенности индекса корреляции проводится так же, как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F- критерию Фишера:
где n -число наблюдений, m -число параметров при переменных х. Во всех рассмотренных нами случаях, кроме полиномиальной регрессии, m =1, для полиномов (34) m=k, т.е. степени полинома. Величина т характеризует число степеней свободы для факторной СКО, а (п-т-1) - число степеней свободы для остаточной СКО. Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем больше разница между R2 и r2. Близость этих показателей означает, что усложнять форму уравнения регрессии не следует и можно использовать линейную функцию. Практически, если величина (R2-r2) не превышает 0,1, то линейная зависимость считается оправданной. В противном случае проводится оценка существенности различия показателей детерминации, вычисленных по одним и тем же данным, через t -критерий Стьюдента:
Здесь в знаменателе находится ошибка разности (R2-r2), определяемая по формуле:
Если t >tтабл(α;n-m-1), то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна. В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.249.105 (0.032 с.) |
 называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки
называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки  :
: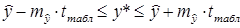 (30)
(30)
 зависит от ошибки
зависит от ошибки  и ошибки коэффициента регрессии b, т.е.
и ошибки коэффициента регрессии b, т.е. 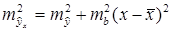 .
. .
.
 .
.
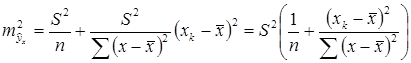
 (31)
(31) достигает минимума при
достигает минимума при  и возрастает по мере удаления
и возрастает по мере удаления 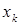 от
от  в любом направлении.
в любом направлении.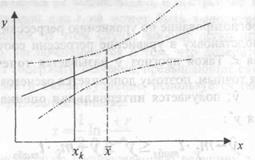
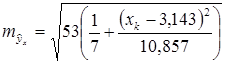
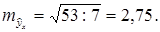 При хk= 4
При хk= 4
 , (32)
, (32) но и случайную ошибку S. Таким образом, средняя ошибка прогноза индивидуального значения y составит:
но и случайную ошибку S. Таким образом, средняя ошибка прогноза индивидуального значения y составит: (33)
(33)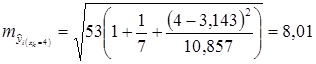
 = -5,79 + 36,84 • 8 = 288,93. Предполагаемое значение - 250. Средняя ошибка прогнозного индивидуального значения:
= -5,79 + 36,84 • 8 = 288,93. Предполагаемое значение - 250. Средняя ошибка прогнозного индивидуального значения:

 (34)
(34) (35)
(35) (36)
(36) .
. (37)
(37) (38)
(38) (39)
(39) (40)
(40) (41)
(41) (42)
(42)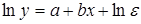 (43)
(43) (44)
(44) . Если Е удовлетворяет условиям Гаусса-Маркова, параметры уравнения (40) оцениваются по МНК из уравнения (44). Уравнение (41) приводится к виду:
. Если Е удовлетворяет условиям Гаусса-Маркова, параметры уравнения (40) оцениваются по МНК из уравнения (44). Уравнение (41) приводится к виду: (45)
(45) (48)
(48) (50)
(50) (51)
(51) (52)
(52)
 (53)
(53) - общая дисперсия результативного признака у,
- общая дисперсия результативного признака у,  остаточная дисперсия, определяемая по уравнению нелинейной регрессии
остаточная дисперсия, определяемая по уравнению нелинейной регрессии  . Следует обратить внимание на то, что разности в соответствующих суммах
. Следует обратить внимание на то, что разности в соответствующих суммах  и
и  берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. По-другому (53) можно записать так:
берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. По-другому (53) можно записать так: (54)
(54) (55)
(55) (56)
(56) (57)
(57)







