
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення об'єму піраміди: з імли століть
Давні єгиптяни. Піраміда з давніх-давен привертала увагу допитливих шукачів істини. В одній з небагатьох пам'яток математичної культури давніх єгиптян, що дійшли до нас, — так званому Московському папірусі (назва походить від місця теперішнього його зберігання) — міститься фрагмент, присвячений обчисленню об'єму зрізаної піраміди. Ось переклад цього фрагмента: «Якщо тобі називають піраміду 6 ліктів висотою, 4 лікті в нижній стороні і 2 лікті у верхній стороні, то обчислюй з цими 4, піднісши їх до квадрата; одержується 16. Подвоївши 4, матимеш 8. Обчислюй з цими 2, піднісши їх до квадрата; матимеш 4. Склади ті 16 з тими 8 і з цими 4; матимеш 28. Розділи 6 на 3; матимеш 2. Обчисли 28 двічі; матимеш 56. Дивись: вона є 56. Ти знайшов правильно». Неважко зрозуміти, що тут йдеться про обчислення об'єму зрізаної піраміди з квадратними основами розмірами 4×4 та 2×2 лікті і висотою 6 ліктів, і що це обчислення здійснюється цілком відповідно до правильної для цього випадку формули Яким же чином прадавній жрець-математик міг одержати такий феноменальний результат? Про це зараз можна лише гадати. Наявні пам'ятки про це не сповіщають. Існує декілька вірогідних гіпотез. Демокріт і Кавальєрі. Демокріт з міста Абдери жив у V ст. до н.е. і прославився як один з найвпливовіших грецьких філософів. Кредом його філософії природи була гіпотеза про існування найдрібніших неподільних структурних елементів речовини — так званих атомів. Гіпотеза ця в різні епохи то заперечувалася, то відновлювалася знову, і в цілому справила і продовжує справляти величезний вплив на розвиток наукових ідей. Жодної праці самого Демокріта до нас не дійшло. Залишилися лише свідчення пізніших учених, зокрема Архімеда, які сповіщають, що свої атомістичні фізичні уявлення Демокріт поширював на геометрію і що це дало йому змогу вивести формулу для обчислення об'єму піраміди. Геометричні тіла Демокріт уявляв складеними з тонких паралельних пластинок, товщина яких рівна одному атому. Як насправді можна було зробити цю ідею результативною, ми можемо побачити на прикладі «Геометрії» Кавальєрі, в якій через багато століть і були реалізовані прадавні атомістичні ідеї Демокріта.
Припустимо, що площі основ цих фігур містять по Відповідно до атомістичного принципу, відношення цих сум Архімед. Уже наводилося схвальне свідчення Лейбніца про «Геометрію» Кавальєрі. І справді, дуже небагато треба, щоб розвинути ідею Кавальєрі, а точніше Демокріта, до цілком строгого виведення формули для об'єму піраміди. Цікаво, що це було зроблено ще задовго до Кавальєрі великим ученим античності і палким поціновувачем Демокріта Архімедом. Чим недосконале виведення Демокріта-Кавальєрі? Тим, що в ньому піраміда підміняється внутрішнім «ребристим» тілом, але не показується, що сумарний об'єм «зазубринок», які містяться між ним і поверхнею піраміди, із збільшенням кількості цих «зазубринок» прямує до нуля. От якби побудувати ще й подібне зовнішнє ребристе тіло, яке охоплює дану піраміду, і показати, що і його об'єм із збільшенням кількості «зазубринок» прямує до того ж граничного значення, що й об'єм внутрішнього тіла, от тоді вже потрібний висновок був би належним чином аргументований (і то залишилася б ще «проблемка» у випадку ірраціональної площі основи піраміди). Це й здійснив Архімед. Його виведення формули для об'єму трикутної піраміди з незначними модифікаціями і досі часто відтворюється в підручниках з елементарної геометрії.
Неважко помітити, що многогранник Зупинимося на першому варіанті (при ньому зручніше застосувати формулу для суми квадратів натуральних чисел, уже наведену вище у зв'язку з розглядом методу Кавальєрі). Побудовані перерізи піраміди віддалені від її вершини відповідно на
При необмеженому зростанні п ця величина прямує до значення Третя проблема Гільберта. Уже саме різноманіття підходів до обчислення об'єму піраміди засвідчує неелементарність цієї проблеми. А ідеалом було досягнути повної аналогії зі встановленням формули для площі трикутника. Зробити цього не вдалося. Взагалі, аналогії між площами і об'ємами сягають доволі далеко — від самих означень до обчислень об'ємів прямокутного і довільного похилого паралелепіпеда, навіть призми, яку ще можна вважати аналогом паралелограма. Проте, при переході до тетраедра аналогії у виведенні формул втрачаються. Площа трикутника знаходиться шляхом доповнення його до паралелограма або прямокутника. Знайти аналогічними перебудовами об'єм тетраедра — просторового аналога трикутника — нікому не вдавалося. Кожний знайдений спосіб, зокрема і ті, що наведені в цьому підручнику, в явній чи неявній формі передбачали здійснення граничного переходу у нескінченних послідовностях многогранників, якими наближався даний тетраедр. У виведенні на основі принципу Кавальєрі, наприклад, цей перехід закладений в обґрунтуванні самого принципу, а у виведенні «методом вичерпування» — в самому цьому методі. То може в цьому є об'єктивна необхідність, може й не можна в загальному випадку обійтися лише скінченними розрізаннями, доповненнями чи іншими якими-небудь перебудовами, щоб перебудувати тетраедр у рівновеликий йому паралелепіпед або бодай в яку-небудь іншу призму і саме на цій основі визначити його об'єм?
Ця проблема стала однією із знаменитих 23-х проблем Гільберта (третьою за списком), які цей видатний математик виділив як «заповіт дев'ятнадцятого століття двадцятому». Давид Гільберт (1862-1943) був одним з найвидатніших математиків усіх епох, «останнім енциклопедистом у галузі математики», тобто дослідником, інтереси і вагомі наукові результати якого обіймали практично усю сучасну йому математичну науку. Закінчив Кенігзберзький університет (тепер російське місто Калінінград). У 1895—1930 рр. — професор Ґеттінґенського університету. У 1930 р. у віці 68 років, як і належало німецькому професорові, пішов у відставку. Але ще три роки продовжував читати лекції — аж до приходу до влади в Німеччині нацистів — у 1933р. Після цього повністю залишив викладання. За прикладом Гільберта університет залишило більшість викладачів-євреїв. «Математика в Геттінгені? Так вона ж там уже просто не існує», — з сумом відповідав Гільберт на запитання нацистського міністра. Тривала наукова кар'єра Гільберта доволі чітко поділяється на ряд періодів, присвячених роботі в якій-небудь одній галузі математики. Роки з 1898 по 1902 були віддані основам елементарної геометрії. В той час завдяки відкриттю неевклідових геометрій уже було зрозуміло, наскільки важливою є аксіоматична база в геометрії, адже різні аксіоми можуть давати і різні геометрії. Тому проводилися інтенсивні дослідження з метою виділити мінімальну, але водночас і повну систему аксіом, з якої ця евклідова геометрія могла б бути виведена суто логічним шляхом, тобто без будь-якого явного чи прихованого посилання на рисунки або які-небудь інші інтуїтивні просторові уявлення. Остаточний підсумок цим дослідженням підвів саме Гільберт. У 1899р. він опублікував книгу «Основи геометрії», в якій дав повне вирішення цієї віковічної проблеми, започаткованої ще «Началами» Евкліда. Зовсім недавно, у 1999 р., минуло лише 100 років з часу опублікування цієї праці. Отже, геометрія — водночас і давня, і молода наука. Усі аксіоми геометрії (планіметрії і стереометрії разом) Гільберт розбив на 5 груп. Першу групу складають аксіоми належності, другу — аксіоми порядку (або розміщення), третю — аксіоми рівності (відрізків, кутів і трикутників), четверту — аксіоми неперервності і п'яту — одна-єдина аксіома паралельності. Всього 20 аксіом. Усі ці аксіоми з більшою чи меншою повнотою приймаються в переважній більшості сучасних шкільних підручників з геометрії.
У русло досліджень Гільберта з основ геометрії потрапила, звичайно, і проблема вимірювання об'єму піраміди, яку він включив навіть до числа 23-х своїх знаменитих «проблем Гільберта». Для наукової творчості Гільберта особливо характерною була віра в глибоку ідейну єдність усіх математичних наук і напрямків, у спорідненість математичних і загальноприродничих проблем, впевненість у необмеженій можливості людського розуму. Зібрання наукових праць Д. Гільберта, видане під його особистим наглядом у 1932 - 1935 роках, закінчувалося статтею «Пізнання природи», а ця стаття — лозунгом: «Ми повинні знати — ми будемо знати!» Свою знамениту доповідь, в якій вперше були сформульовані проблеми Гільберта, сам Гільберт прочитав у серпні 1900 року в Парижі на Другому Міжнародному конгресі математиків. А вже через рік третя проблема була розв'язана учнем Гільберта Максом Деном (1878-1952) (деякі з проблем Гільберта не розв'язані і досі). Ден встановив необхідні умови, за яких многогранник одного виду можна перебудувати у рівновеликий йому многогранник іншого виду. Тетраедр і призма цим умовам задовольняють не завжди. Отже, в загальному випадку вивести формулу для об'єму тетраедра без здійснення в тій чи інші формі граничного переходу неможливо. Коли Макс Ден зайнявся третьою проблемою Гільберта, йому не було ще й 22 років, і він мабуть ще добре пам'ятав той час, коли сам вивчав шкільну геометрію. Пам'ятав... і продовжував любити її.
«Кубок Кеплера»
Зрештою, деякі міркування Платона можна інтерпретувати і так, що форму додекаедра мала п'ята, придумана ним стихія — божественний ефір. Пізніше ідея ефіру хвилювала учених протягом багатьох століть, поки врешті-решт не була повністю відкинута з відкриттям на початку XX ст. спеціальної теорії відносності. Але ще й досі чується її відгомін, наприклад, у висловах «в ефірі», «ефірний час» тощо.
Платон мріяв осягнути таємницю взаємоперетворень речовин, встановивши закономірності геометричних перебудов елементів основних стихій. І це, по суті, була одна з перших спроб математичного моделювання в природознавстві. До Платона таким моделюванням займалися піфагорійці. Але їхні моделі були в основному числовими. Наприклад, гармонічно співзвучні акорди піфагорійці пов'язували з пропорційністю довжин струн певним відношенням цілих чисел. Платон же одним з перших запропонував змістовну геометричну модель. А його авторитет сприяв тому, що ця ідея завжди приваблювала дослідників. На початку доби нового дослідного природознавства до ідеї використання правильних многогранників у моделюванні природи звернувся знаменитий німецький астроном Йоганн Кеплер (1572-1630). Результатом його пошуків стало декілька так званих «кубків Кеплера», якими символізувалися гармонійні закономірності в розташуванні планетних орбіт. Найвідоміший з «кубків Кеплера» відтворено вище. При його створенні Кеплер виходив ще з давньої гіпотези про рух планет навколо Сонця по кругових орбітах. Весь кубок обмежує велика сфера, якій відповідає орбіта найвіддаленішої з відомих тоді планет — Сатурна. Якщо в цю сферу вписати куб, а в куб — знову сферу, то, за Кеплером, матимемо сферу Юпітера. У сферу Юпітера вписується правильний тетраедр, а вписаною в тетраедр сферою визначається орбіта Марса. Далі послідовно вписується додекаедр, ікосаедр та октаедр, а відповідні вписані сфери визначають орбіти Землі, Венери та Меркурія. Пізніше, з відкриттям Кеплером справжніх законів руху планет навколо Сонця, перший з яких стверджує, що траєкторіями цього руху є не кола, а еліпси, а ще пізніше — з відкриттям нових планет Плутона і Нептуна, — «кубок Кеплера», а разом з ним і правильні многогранники втратили свій колишній ореол таємничості.
Кавальєрі (1598-1647) Бонавентура Кавальєрі народився в Мілані наприкінці XVI ст. в одному з найзнатніших, але збіднілому сімействі. В юнацькі роки він отримав прекрасну гуманітарну освіту. Тому-то навіть у своїх суто математичних працях Кавальєрі часто застосовує найвишуканіші класичні звороти і метафори. Ось як, наприклад, починається передмова до «Геометрії» Кавальєрі: «Подібно до того, як незліченному рою бджіл, що навперебій вражають своїми жалами, не вдається відігнати ведмедя, який впивається медом, якщо він хоч трохи скуштував схованих в дереві солодощів, так само, звичайно, не знайдеш того, хто, хоч краєчком губ попробувавши солодощів математичних доведень (яка б сила щонайбільших труднощів, якими ці доведення супроводжуються, не відштовхувала його, ніби частими уколами жал), не прагнув би всіма силами опанувати їх цілком, до повного насичення. О, друже читачу, що звик куштувати ці медові страви! Я пропоную тобі, палаючому пристрастю до цих солодощів, скуштувати плодів, які виросли в мене під час моїх геометричних досліджень». Ще юнаком Кавальєрі вступив у чернечий орден ієронімітів. Монастир св. Ієроніма знаходився поблизу його дому, і монахи, з якими він постійно зустрічався, справили визначальний вплив на напрямок його освіти. Приблизно у 18-річному віці Кавальєрі перейшов у монастир ієронімітів у Пізі — рідному місті знаменитого Галілея. У Пізі Кавальєрі зблизився з відомим тоді тамтешнім математиком Кастеллі, який, запримітивши в юнакові виняткове математичне обдарування, спочатку сам направляв його розвиток у потрібне русло, а потім познайомив з самим Галілеєм. Той, переконавшись у справедливості захоплених відгуків Кастеллі, спочатку певний час настановляв Кавальєрі, а коли в 1629 р. в Болоньї з'явилася вакансія по кафедрі математики, написав для нього захоплену рекомендацію, в якій молодий математик ставився «в рівень з Архімедом». Разом з рукописом «Геометрії» цієї рекомендації виявилося досить для зайняття вакансії. На цій посаді з великою шаною Кавальєрі перебував до кінця своїх земних днів. Він написав ще декілька об'ємних і змістовних математичних праць. Але жодна з них з погляду майбутнього уже не зрівнялася з «Геометрією неподільних». Пам'ятник Кавальєрі поставлено у Мілані в 1844 р. В лівій руці — сфера, на якій зображено сферичний трикутник АВС і записано відношення
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.42 (0.051 с.) |
 , де а, b — сторони квадратних основ піраміди, Н — її висота. Формула справді правильна, бо є частковим випадком формули
, де а, b — сторони квадратних основ піраміди, Н — її висота. Формула справді правильна, бо є частковим випадком формули  для випадку, що розглядається у фрагменті.
для випадку, що розглядається у фрагменті. Нехай маємо піраміду і призму, наприклад, трикутні (рис. 1) з рівновеликими основами і рівними висотами. Позначимо через
Нехай маємо піраміду і призму, наприклад, трикутні (рис. 1) з рівновеликими основами і рівними висотами. Позначимо через  ,
,  їхні об'єми.
їхні об'єми. квадратних одиниць. Поділимо їхні висоти на п рівних частин і через точки поділу проведемо площини, паралельні основі. Тоді сума площ трикутників, що утворилися в перерізі піраміди, разом з основою становитиме
квадратних одиниць. Поділимо їхні висоти на п рівних частин і через точки поділу проведемо площини, паралельні основі. Тоді сума площ трикутників, що утворилися в перерізі піраміди, разом з основою становитиме  квадратних одиниць. В алгебрі доводиться, що це число дорівнює
квадратних одиниць. В алгебрі доводиться, що це число дорівнює  . Сума ж площ відповідних перерізів призми дорівнюватиме
. Сума ж площ відповідних перерізів призми дорівнюватиме  квадратних одиниць.
квадратних одиниць. приймається за наближене значення відношень об'ємів даних фігур. Причому, — наближення тим точніше, чим більше число п. Оскільки квадратні одиниці для вимірювання площ можна як завгодно подрібнювати, то й число n можна зробити як завгодно великим. За рахунок цього число
приймається за наближене значення відношень об'ємів даних фігур. Причому, — наближення тим точніше, чим більше число п. Оскільки квадратні одиниці для вимірювання площ можна як завгодно подрібнювати, то й число n можна зробити як завгодно великим. За рахунок цього число  можна зробити як завгодно малим. Тому
можна зробити як завгодно малим. Тому  . Таким чином,
. Таким чином,  . Знаючи формулу
. Знаючи формулу  для об'єму призми, звідси легко одержується формула для об'єму піраміди:
для об'єму призми, звідси легко одержується формула для об'єму піраміди:  .
. Ось це виведення. Нехай маємо довільну трикутну піраміду Р, S — площа її основи, Н — висота. Поділимо одне з бічних ребер на n рівних частин і побудуємо перерізи піраміди площинами, що проходять через точки поділу паралельно основі (рис. 2). Цими площинами, зокрема, поділиться на п рівних частин завдовжки
Ось це виведення. Нехай маємо довільну трикутну піраміду Р, S — площа її основи, Н — висота. Поділимо одне з бічних ребер на n рівних частин і побудуємо перерізи піраміди площинами, що проходять через точки поділу паралельно основі (рис. 2). Цими площинами, зокрема, поділиться на п рівних частин завдовжки  i висота піраміди. Побудуємо, далі, на кожному з перерізів, а також і на основі піраміди, — призми, у кожній з яких одне з бічних ребер належить вибраному бічному ребру піраміди, а інші два бічних ребра «виходять» за дану піраміду. Сукупність усіх цих п призм утворить східчастий многогранник, відомий в учнівських колах як «чортова драбина» (позначимо його через G), який містить у собі дану піраміду Р. Отже,
i висота піраміди. Побудуємо, далі, на кожному з перерізів, а також і на основі піраміди, — призми, у кожній з яких одне з бічних ребер належить вибраному бічному ребру піраміди, а інші два бічних ребра «виходять» за дану піраміду. Сукупність усіх цих п призм утворить східчастий многогранник, відомий в учнівських колах як «чортова драбина» (позначимо його через G), який містить у собі дану піраміду Р. Отже,  . Приймемо, нарешті, кожний з перерізів піраміди за верхню основу трикутної призми і побудуємо аналогічним чином п- 1 таку призму, кожна з яких повністю належить піраміді. Многогранник, утворений цими призмами, позначимо через
. Приймемо, нарешті, кожний з перерізів піраміди за верхню основу трикутної призми і побудуємо аналогічним чином п- 1 таку призму, кожна з яких повністю належить піраміді. Многогранник, утворений цими призмами, позначимо через  . Зрозуміло, що
. Зрозуміло, що 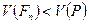 . Таким чином,
. Таким чином, . (*)
. (*) відрізняється від многогранника
відрізняється від многогранника  лише на одну нижню призму, об'єм якої дорівнює
лише на одну нижню призму, об'єм якої дорівнює  . Збільшуючи п, цю величину можна зробити як завгодно малою. З нерівностей (*) випливає, що тоді різниці значень об'ємів
. Збільшуючи п, цю величину можна зробити як завгодно малою. З нерівностей (*) випливає, що тоді різниці значень об'ємів  та
та  будуть також як завгодно малими. Отже, шуканий об'єм
будуть також як завгодно малими. Отже, шуканий об'єм  можна знаходити і як границю послідовності
можна знаходити і як границю послідовності  ,і як границю послідовності
,і як границю послідовності  .
. частину висоти піраміди. Тому їхні площі дорівнюють
частину висоти піраміди. Тому їхні площі дорівнюють  частини площі основи піраміди. Отже, для об'єму многогранника
частини площі основи піраміди. Отже, для об'єму многогранника 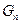 маємо вираз:
маємо вираз: .
. Отже,
Отже,  що й треба було довести.
що й треба було довести. Правильні многогранники — тетраедр, куб, октаедр, ікосаедр, додекаедр — були відомі задовго до Евкліда. Ще піфагорійці, тобто учні і послідовники легендарного Піфагора, перші з яких жили щонайменше за 200 років до Евкліда, вміли будувати принаймні перші чотири з цих фігур. Відкриття додекаедра багато хто приписує філософу Платону, що також жив до Евкліда. Саме завдяки Платону правильні многогранники набули величезної притягальної сили, оскільки відігравали ключову роль у його філософії природи. За Платоном, усе суще в природі утворилося в результаті взаємодії вогню, повітря, води і землі. Найдрібніші структурні елементи (атоми) цих стихій мають форми відповідно правильного тетраедра, октаедра, ікосаедра і куба. Оскільки незадіяним залишався додекаедр, то Платон вважав, що форму цієї фігури має весь Всесвіт. Уже в наш час цю ідею використав відомий іспанський художник-сюрреаліст Сальвадор Далі, зобразивши у своїй «Таємній вечері» знаменитий біблійний сюжет на фоні Всесвіту — додекаедра.
Правильні многогранники — тетраедр, куб, октаедр, ікосаедр, додекаедр — були відомі задовго до Евкліда. Ще піфагорійці, тобто учні і послідовники легендарного Піфагора, перші з яких жили щонайменше за 200 років до Евкліда, вміли будувати принаймні перші чотири з цих фігур. Відкриття додекаедра багато хто приписує філософу Платону, що також жив до Евкліда. Саме завдяки Платону правильні многогранники набули величезної притягальної сили, оскільки відігравали ключову роль у його філософії природи. За Платоном, усе суще в природі утворилося в результаті взаємодії вогню, повітря, води і землі. Найдрібніші структурні елементи (атоми) цих стихій мають форми відповідно правильного тетраедра, октаедра, ікосаедра і куба. Оскільки незадіяним залишався додекаедр, то Платон вважав, що форму цієї фігури має весь Всесвіт. Уже в наш час цю ідею використав відомий іспанський художник-сюрреаліст Сальвадор Далі, зобразивши у своїй «Таємній вечері» знаменитий біблійний сюжет на фоні Всесвіту — додекаедра. , що характеризує площу цього трикутника. Сферична геометрія вважалася основним об'єктом досліджень Кавальєрі.
, що характеризує площу цього трикутника. Сферична геометрія вважалася основним об'єктом досліджень Кавальєрі.


