Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 1 . Правило сложения и умноженияСтр 1 из 4Следующая ⇒
Вопрос 36. центральная предельная теорема. Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом. А поскольку случайные величины всегда порождаются бесконечным количеством причин и чаще всего ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено нормальному закону распределения. Вопрос 11 часть 1 условная вероятность часть 2 теорема умножения часть 1 условная вероятность Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Условной вероятностью Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
В частности, отсюда получаем Часть 2 теорема умножения Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2,..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
Вопрос 25. дисперсия Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/ k ². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три. Определение Пусть
где символ [Замечания § Если случайная величина
§ Дисперсия является вторым центральным моментом случайной величины; § Дисперсия может быть бесконечной. См., например, распределение Коши. § Дисперсия может быть вычислена с помощью производящей функции моментов
§ Дисперсия целочисленной случайной величины может быть вычислена с помощью производящей функции последовательности. Свойства Дисперсия любой случайной величины неотрицательна:
Вопрос 15.Схема Бернулли. В научной и практической деятельности постоянно приходиться проводить многократно повторяющиеся испытания в сходных условиях (физический и технический эксперимент, метеорология, организация производства и т.д.). Как правило при этом результаты предшествующих испытаний никак не сказываются на последующих. Простейший тип таких испытаний состоит в том, что в каждом из испытаний некоторое событие А может появиться с одной и той же вероятностью p и эта вероятность остается одной и той же независимо от результатов предшествующих и последующих испытаний. Этот тип событий называют схемой Бернулли(по имени исследователя Якоба Бернулли). Схема Бернулли положила начало многим дальнейшим построениям и обобщениям теории вероятностей. Пусть проводится серия из n независимых испытаний в каждом из которых с вероятностью p может наступить некоторое событие А. В схеме Бернулли под элементарным событием принято понимать последовательность наступлений или ненаступлений события А в данной последовательности испытаний.
Вопрос 1.ПРАВИЛО СЛОЖЕНИЯ И УМНОЖЕНИЯ Во многих задачах сложные события, вероятности которых надо найти, удается выразить в виде комбинации других, более простых событий, причем вероятности последних либо заданы, либо непосредственно подсчитываются. В таком случае для решения задач можно использовать формулы, выражающие вероятности суммы и произведения событий через вероятности соответствующих слагаемых и сомножителей. Правила сложения и умножения вероятностей: если события
Из правила сложения вероятностей для двух событий вытекает правило нахождения вероятности противоположного события:
Для произвольных событий A и B имеет место формула:
В случае n слагаемых (n>2) эта формула принимает вид:
Вероятность p(В|А) события В при условии наступления события А по определению равна:
Из этого определения следует формула для вычисления вероятности произведения двух событий:
Для вычисления вероятности произведения n событий (n>2) служит общая формула:
События Правило умножения вероятностей для n событий: если события
Вычисление вероятности суммы событий можно свести к вычислению вероятности произведения противоположных событий по формуле
В частности, если события
Вопрос 3. Размещения. Пусть имеется множество из четырех различных цифр {3,5,7,8}. Необходимо составить всевозможные двузначные числа, каждое из которых состоит из различных цифр.Каждое число является упорядоченным подмножеством, состоящим из двух элементов, данного множества, состоящего из четырех элементов. Перечислим их: 35, 37, 38, 53, 73, 83, 57, 58, 75, 85, 78, 87. Всего таких подмножеств- двузначных чисел получилось 12. Каждое упорядоченное подмножество называется размещением. Определение: Размещением из п элементов по т называется любое упорядоченное подмножество из т элементов множества, состоящего из п элементов.На практике чаще представляет интерес не конкретный вид размещений, а их количество. Следующая теорема дает общую формулу для вычисления размещений.
Теорема: Число размещений из n элементов по m равно
Пример. Сколько можно составить четырехзначных чисел, состоящих из разных цифр, использую все 10 цифр? Решение: В числе важен порядок следования цифр. Следовательно, нужно найти количество размещений из 10 по 4:
Но среди них есть числа с нулем в начале. из полученного значения 5040 необходимо вычесть количество таких чисел. Найдем это количество: т.к. на первом месте стоит о, то оставшиеся три выбираем из 9, т.е.
Искомое количество чисел равно 5040-504=4536.
. Вопрос 2. Перестановки Рассмотрим случай, когда п=т. Такие размещения называются перестановками.
Формулу для определения количества перестановок дает теорема.
Доказательство:
Следовательно, Р n= n! Вопрос 4. Сочетания В размещениях и перестановках важен порядок элементов. Рассмотрим случаи, когда порядок элементов в множествах не учитывается, т.е. случаи составления неупорядоченных множеств. Например:Из чисел 3, 5, 2 составить всевозможные произведения из двух различных множителей. Для произведения справедлив переместительный закон (свойство коммутативности), значит необходимо составить неупорядоченные подмножества из двух элементов множества, состоящего из трех элементов. Такие подмножества называются сочетаниями. Определение: Сочетанием из п элементов по т называется любое неупорядоченное множество из т элементов, которые принадлежат множеству, состоящему из п элементов.
Вернемся к задаче. Составим требуемые произведения:
Как видим, в сочетаниях не учитываются перестановки элементов в каждом построенном подмножестве. Учтем это при доказательстве следующей теоремы.
Доказательство: Число размещений из п по т можно получить следующим образом: выбирать по т элементов, не учитывая порядок. Это есть сочетания из п по т. А затем в каждом подмножестве произвести перестановки. Пользуясь правилом умножения, получим
Откуда имеем:
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.105.215 (0.036 с.) |
 (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.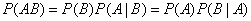 .
.
 ;
; 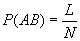 ;
; 


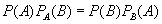


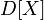 в русской литературе и
в русской литературе и  (англ. variance) в зарубежной. В статистике часто употребляется обозначение
(англ. variance) в зарубежной. В статистике часто употребляется обозначение  или
или  . Квадратный корень из дисперсии, равный
. Квадратный корень из дисперсии, равный  , называетсясреднеквадрати́чным отклоне́нием
, называетсясреднеквадрати́чным отклоне́нием — случайная величина, определённая на некотором вероятностном пространстве. Тогда
— случайная величина, определённая на некотором вероятностном пространстве. Тогда
 обозначает математическое ожидание[1][2].
обозначает математическое ожидание[1][2].
 :
:
 Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; Если случайная величина равна константе, то её дисперсия равна нулю:
Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; Если случайная величина равна константе, то её дисперсия равна нулю:  Верно и обратное: если
Верно и обратное: если  то
то  почти всюду; Дисперсия суммы двух случайных величин равна:
почти всюду; Дисперсия суммы двух случайных величин равна: , где
, где  — их ковариация; Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:
— их ковариация; Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство: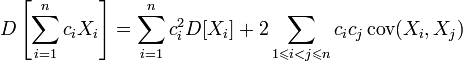 , где
, где  ; В частности,
; В частности,  для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;
для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;


 попарно несовместны, то справедливо равенство
попарно несовместны, то справедливо равенство






 называются независимыми в совокупности, если вероятность любого из них не меняется при наступлении какого угодно числа событий из остальных.
называются независимыми в совокупности, если вероятность любого из них не меняется при наступлении какого угодно числа событий из остальных.



 Доказательство: необходимо заполнить т мест элементами множества из п элементов. Каждое действие- это выбор определенного элемента. Действия совершаются последовательно, значит применимо правило умножения. Первый элемент можно выбрать п способами, второй- (п-1) способами, последний т- ый элемент- (п-(т-1)) способами. Тогда количество размещений равно п(п-1)(п-2)…(п-(т-1)). Умножим и разделим данное выражение на (п-т)!, преобразовав получим более удобный вид:
Доказательство: необходимо заполнить т мест элементами множества из п элементов. Каждое действие- это выбор определенного элемента. Действия совершаются последовательно, значит применимо правило умножения. Первый элемент можно выбрать п способами, второй- (п-1) способами, последний т- ый элемент- (п-(т-1)) способами. Тогда количество размещений равно п(п-1)(п-2)…(п-(т-1)). Умножим и разделим данное выражение на (п-т)!, преобразовав получим более удобный вид:


 Определение: Перестановкой из п элементов называется любое упорядоченное множество, в которое входят по одному разу все п различных элементов данного множества.
Определение: Перестановкой из п элементов называется любое упорядоченное множество, в которое входят по одному разу все п различных элементов данного множества.


 .
.