Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели задач дискретного программирования ⇐ ПредыдущаяСтр 10 из 10
По структуре математической модели задачи дискретного программирования разделяют на следующие классы: 1) задачи с неделимостями; 2) экстремальные комбинаторные задачи; 3) задачи на несвязных и на невыпуклых плоскостях; 4) задачи с разрывными целевыми функциями. Рассмотрим существо некоторых из них. Задачи с неделимостями. Математические модели задач с неделимостями основаны на требовании целочисленности переменных { xi}, вытекающем из физических условий практических задач. К таким задачам относится задача об определении оптимальной структуры производственной программы, где {х1, х2,..., хп} - объемы выпуска продукции. Эта задача заключается в отыскании
при
Если J =N = (1,2,..., n), то задача называется полностью целочисленной, в противном случае, если J≠N - частично целочисленной. Задача о ранце. Одной из наиболее распространенных задач целочисленного программирования является так называемая задача о ранце. Рассмотрим постановку данной задачи. Турист готовится к длительному переходу в горах. В рюкзаке он может нести груз, масса которого не более W. Этот груз может включать в себя п видов предметов, каждый предмет типа j, массой wj, j = 1,2,..., n. Для каждого вида предмета турист определяет его ценность Ej вовремя перехода. Задача заключается в определении количества предметов каждого типа, которые он должен положить в рюкзак, чтобы суммарная ценность снаряжения была максимальной. Обозначим через хj количество предметов j-го типа в рюкзаке. Тогда математическая модель задачи такова:
при ограничениях
Задача о коммивояжере. Имеется (n + 1) город. Задана матрица С = ||cij || расстояний между городами. Выезжая из исходного города Aij, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город Аij. Требуется определить, в каком порядке следует объезжать города, чтобы суммарное пройденное расстояние было минимально. Введем переменные: Xij — 1, если коммивояжер переезжает из населенного пункта А, в Аj; хij - 0 - в противном случае. Математическая модель задачи имеет следующий вид: найти
при условиях
где ui, uj - произвольные целые и неотрицательные числа. Условие (8.20) означает, что коммивояжер выезжает из каждого города один раз, а условие (8.21)- что он въезжает один раз в каждый город.
Если ограничить задачу только условиями (8.20) и (8.21), она будет эквивалентна задаче о назначениях, план которой не обязан быть цикличным. Иначе говоря, путь коммивояжера при этом можно представить как рад несвязанных подциклов, в то время как его путь в действительности состоит из одного цикла. Покажем, что для любого цикла, начинающегося в Aij можно найти ui удовлетворяющие условию (8.22). Пусть ui =p, если коммивояжер посещает город Аi на р- мэтапе. Отсюда следует, что ui- иj ≤ п - 1 для всех i и j, и, таким образом, условие (8.22) выполняется при xij = 0. При хij = 1 условие (8.22) выполняется как строгое равенство: ui-uj+nxij=p-(p+ 1 )+n = n- 1.
8.3. Метод ветвей и границ для задачи целочисленного программирования Рассмотрим частично целочисленную задачу ЛП: минимизировать
при условиях
Процесс поиска оптимального решения начинают с решения непрерывной задачи ЛП. Если полученный при этом оптимальный план Пусть некоторая переменная хi0 (1≤ i0 ≤ т) не получила в плане Если границы изменения хi0 заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи ЛП. Эти задачи состоят в максимизации и минимизации хi0 при условиях (8.24) и (8,25). Теперь для каждого фиксированного целочисленного значения хi0 в найденном отрезке [хi0min, хi0max] находят min z, решая задачу ЛП с ограничениями (8.24), (8.25) и с дополнительным ограничением хi0≤ki0.. Таким образом, все указанные выше возможности можно представить в виде некоторого дерева, в котором вершина 0 отвечает плану
Если оптимальные планы полученных задач удовлетворяют условиям целочисленности, то план с минимальной оценкой Любой маршрут в дереве от начальной вершины 0 до некоторой вершины определяет допустимую последовательность выбора целочисленных решений для переменных. Процесс продолжают до тех пор, пока продолжение ветвления становится невозможным. Каждая конечная вершина отвечает некоторому допустимому целочисленному плану. Вершина с минимальной оценкой дает оптимальный план. Рассмотрим алгоритм решения задачи целочисленного программирования. На первом этапе необходимо задать множество G(0), определяемое условиями (8,24), (8.25). На втором этапе формируются множества xj≤[xj0] или xj≥[ xj0] +1 (8.27) где [xj0]- целая часть хj0. На третьем этапе осуществляется вычисление оценок. Для множества G(0) оценку
где Если множество На четвертом этапе осуществляется нахождение планов. Если план На пятом этапе выполняют ветвление. Ветвление производят в том случае, когда план Пусть
.причем
Укажем некоторые особенности метода ветвей и границ для задач ЦП. 1. Если все коэффициенты сj целевой функции - целые при 1 ≤j≤ni и равны нулю при j > ni, то оценку 2. Алгоритм метода в вычислительном отношении представляет собой последовательность задач ЛП, причем конечность алгоритма следует из предполагаемой ограниченности множества G. 3. Из описания -алгоритма следует, что в применении метода ветвей и границ для полностью целочисленных и для частично.целочисленных задач нет никакой разницы. Геометрически этот метод можно интерпретировать таким образом. Гиперплоскость, определяемая функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи ЛП до встречи с ближайшей целочисленной точкой этого многогранника. ■ Пример 1 применения метода ветвей и границ для решения задач дискретного программирования. Возьмем задачу Максимизировать 3 x1 +3 x2 +13 x3 При ограничениях -3 x1+6 x2+7x3≤8; 6 x1-3 x2 +7x3≤8; где каждая переменная xj должнабыть неотрицательным целым. Предположим, что заданы границы на каждую переменную:
0≤ xj≤5, j=1,2,3. Как принято, обозначим x0t значение целевой функции. На итерации 1 примем нижнюю границу x 01 , поскольку при всех xj =0 имеем допустимое решение. Основой список содержит лишь одну задачу линейного программирования (8,) (9) и (10), которую назовем задачей 1. Выберем эту задачу на шаге 1 и найдем ее оптимальное решение на шаге 2: x0=16, x1=x2= Поскольку решение не является целочисленным, перейдем от шага 3 к шагу 4 и выберем x1. Внесем далее в основной список Задачу 2: ограничения (9) 3≤x1≤5; 0≤x2≤5; 0≤x3≤5; Задачу 3: ограничения (9) 0≤x1≤2; 0≤x2≤5; 0≤x3≤5; Допустимое решение задачи 2 отсутствует. Поэтому выберем x02= x03=0 и вернемся к шагу 1. выберем теперь задачу 3 и получим на шаге 2 оптимальное решение, x0=
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.13.173 (0.032 с.) |
 (8.13)
(8.13)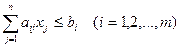 (8.14)
(8.14)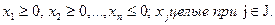 (8.15)
(8.15)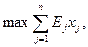 (8.16)
(8.16)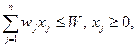 xj -целое, i= 1,2,..., т. (8.17)
xj -целое, i= 1,2,..., т. (8.17)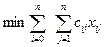 (8.19)
(8.19)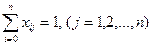 ; (8.20)
; (8.20)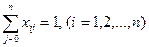 ; (8.21)
; (8.21)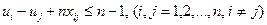 , (8.22)
, (8.22)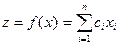 (8.23)
(8.23)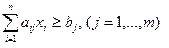 ; (8.24)
; (8.24)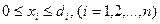 ; (8.25)
; (8.25) - целые числа. (8.26)
- целые числа. (8.26)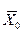 не удовлетворяет условию (8.26), то значение целевой функции
не удовлетворяет условию (8.26), то значение целевой функции 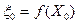 дает нижнюю оценку для искомого решения, т.е.
дает нижнюю оценку для искомого решения, т.е. 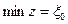 .
. , для всех k.
, для всех k.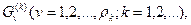 задаваемые условиями (8.24), (8.25) и дополнительным условием
задаваемые условиями (8.24), (8.25) и дополнительным условием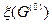 определяют как
определяют как 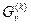 оценку
оценку 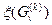 определяют аналогично:
определяют аналогично:
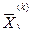 -оптимальный план задачи с условиями (8.24), (8.25) и с дополнительным условием (8.27).
-оптимальный план задачи с условиями (8.24), (8.25) и с дополнительным условием (8.27). ∞.
∞.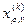 - одна из нецелочисленных компонент плана, где 1 ≤ρ≤n1, тогда множество
- одна из нецелочисленных компонент плана, где 1 ≤ρ≤n1, тогда множество 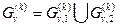

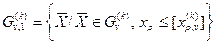 ; (8.28)
; (8.28)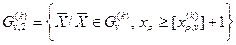 (8.29)
(8.29)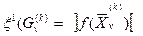 , где ]а[ обозначено наименьшее целое, но не меньшее, чем а, т.е. округленное до ближайшего целого с избытком.
, где ]а[ обозначено наименьшее целое, но не меньшее, чем а, т.е. округленное до ближайшего целого с избытком.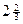 , x3=0.
, x3=0.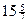 , x1=x2=2, x3=
, x1=x2=2, x3= 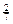 , не являющееся целочисленным. Дальнейшее решение задачи показано на рис.
, не являющееся целочисленным. Дальнейшее решение задачи показано на рис.