
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виміри лінійних об’єктів та полігонів.
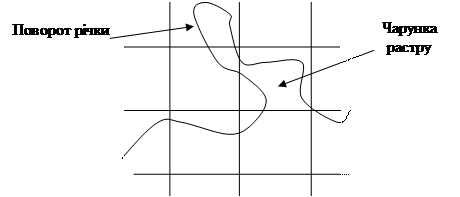
Під час досліджень за допомогою геоінформаційної системи нам потрібно знати, що це за об’єкти, де і в якій кількості вони є, їх розміри, як далеко вони від нас і яка відстань між ними, тощо. Крім того, потрібно вимірювати параметри об’єктів: довжину, ширину, площу, а також взаємозв’язки між цими параметрами (характеристиками, що були виміряні). Це нам дасть кількісні характеристики об’єктів, які ми можемо далі використовувати в аналізі для порівняння об’єктів в межах одного покриття, а також для порівняння між покриттями. Тому необхідно більш докладно розглянути механізми виконання наведених операцій. Спочатку розглянемо більш докладно основні види вимірів лінійних об’єктів та полігонів. Чому так? Ми знаємо, що крім поверхні існує три типи об’єктів: точкові, лінійні, площинні. Точки не мають просторових вимірів, лінії одновимірні, області мають два виміри: довжину і ширину. Оскільки точки не мають просторової протяжності (а тільки значення атрибутів), то вони не підлягають нашому подальшому розгляду. Вимірювання довжини лінійних об’єктів. Лінії мають одну міру величини – довжину, якщо не враховувати значення інших атрибутів, які можна просто вибрати з бази даних. Але довжина лінії також може використовуватися в якості атрибуту, за яким може проводитися класифікація об’єктів. Визначення довжини вертикальних або горизонтальних ліній в растрі виконується підрахунком кількості чарунок, через які лінія проходить і множенням цього значення на розмір однієї чарунки растру (дозвільна спроможність). Більш удосконалені геоінформаційні системи використовують тригонометричні функції для визначення дійсної довжини лінії, яка має довільну орієнтацію. Більш складна проблема виникає у випадку, коли ми маємо справу з крученою лінією, що випадковим чином проходить по растру (рис. 4.4).
В такому випадку довжина цієї лінії буде зменшена незалежно від методу її визначення. Це буде обумовлено тим, що окремі цілі закрути річки будуть розміщуватися у межах однієї чарунки растру. Тому для виміру лінійних об’єктів потрібно використовувати векторну структуру даних.
Визначення довжини лінійного об’єкту у векторній системі більш точніше (як і саме подання лінії), ніж підрахування чарунок растру. Для кожного прямого відрізку, що утворює лінію, система зберігає координати крайніх точок, з яких за теоремою Піфагора може бути підрахована довжина цього відрізку. Склавши значення довжини всіх відрізків лінії, ми отримаємо точне значення її загальної довжини. Але необхідно пам’ятати, що векторне подання лінійних об’єктів також використовує свого роду дискретизацію, коли криві ділянки апроксимуються прямими відрізками, і чим більше таких відрізків використовується, тим точніше подання цього об’єкту в цій структурі даних і тим точніше буде отримане значення загальної довжини лінії. Вимірювання полігонів. Площинні об’єкти двовимірні, тому ми можемо надавати їм більше характеристик. Наприклад: довжина і ширина; довжина кордонів полігону; площа полігону. Всі ці характеристики можуть використовуватися в якості обчислюємих атрибутів для класифікації областей за розмірами. Крім того користувачі можуть їх використовувати просто для створення окремих покрить (шарів) полігональних об’єктів встановлених розмірів. Лінійні міри полігонів. Однією з характеристик полігонів, яка дуже важлива при проведенні їх аналізу, є орієнтація. Для її визначення потрібно встановити напрям найбільш довгої вісі об’єкту. Більшість растрових ГІС не мають такої функції. У векторній моделі даних таке рішення полягає у визначенні відстані між точками кожної пари протилежних вершин. Найбільша відстань відповідає більшій вісі полігону, а її кутова орієнтація (напрям) визначається методами сферичної тригонометрії. Відповідно, але вже як мінімальне значення, знаходиться мала вісь полігону. Крім того, іноді аналітику потрібна не орієнтація, а співвідношення між великою і малою віссю. Її значення дає просту міру форми, яка може застосовуватися для виділення об’єктів з заданим співвідношенням вісь. Визначення периметру. Визначення периметру полігону полягає в складанні довжини відрізків, що утворюють його границю, і які можуть бути отримані за допомогою теореми Піфагора. У растровій моделі даних цей процес виконується складніше. Для цього потрібно виділити всі чарунки, що утворюють периметр, підрахувати їх кількість та помножити це значення на дозвільну спроможність растру. Як і у випадку з лініями, чим складніше границя полігону тим нижче точність обчислення.
Обчислення площини полігону. У растровій моделі площа підраховується простим множенням площі чарунки растру на кількість чарунок, які займає область. У випадку визначення площі одного чи кількох полігонів, що утворюють фрагментований регіон одного атрибуту, процес визначення ускладнюється. В такому випадку ми спочатку повинні перекласифікувати потрібні групи чарунок таким чином, щоб вони отримали унікальний атрибут. А далі вже безпосередньо здійснюють процес визначення площі. Крім того, коли об’єкт має складну форму, то його спочатку розподіляють на прості фігури для яких нескладно визначити площу (трикутник, коло, квадрат, тощо). А вже після цього виконується складання всіх отриманих значень площ. У більшості векторних геоінформаційних систем площі полігонів підраховуються при їх вводі і заносяться у таблиці атрибутів, що спрощує подальші процеси аналізу. Для цього потрібно тільки вибрати відповідне значення з бази даних. Іноді використовується для завдань аналізу значення відношення периметр/площа області, яка є найбільш стисненою характеристикою форми та мірою складності полігону. Найменше значення буде мати круг, а в той же час витягнуті полігони мають більше значення цього відношення. Міри форми. Ми встановили, що існує тісний зв’язок між формою і такими мірами, як периметр і площа для полігонів та довжина для лінійних об’єктів. В багатьох випадках окреслення об’єктів (полігонів) і міра хвилястості лінійних об’єктів забезпечують поняття взаємовідносин між об’єктами та їх оточенням. Наприклад хвилястість річки пов’язана: з обсягом осадку, що вона переносить, витратою води (дебіт), тощо. Тому розглянемо міри форми, що є у більшості сучасних геоінформаційних систем. Вимірювання хвилястості. На практиці існує дві прості міри хвилястості, які можуть використовуватися для характеристики ліній. Перша – це відношення загальної довжини відрізків, що утворюють лінію, до відстані між її крайніми точками. Чим ближче це відношення до одиниці, тім менше хвиляста ця лінія (для прямої лінії це значення дорівнює 1). Але часто про форму кривої лінії потрібно знати більше. Для цього в кожне закруглення вписують коло та вимірюють його радіус. У випадку, якщо річка подана полігоном, то є можливість ще виміряти відношення радіуса до ширини річки, яке дає нам ще одну корисну характеристику форми. Міри форми полігонів. Як ми бачимо, існують два основних аспекти вимірювання. Перший, на основі ідеї перфорованих і фрагментованих регіонів, має загальну назву просторової цілісності. Друга характеристика – на основі ідеї конфігурації границі, базується на відношенні периметра і площі. Найбільш поширеною мірою просторової цілісності полігону є функція Ейлера, яка дозволяє подати числове вираження ступеню фрагментованості і перфорованості. Функція Ейлера зіставляє кожній конфігурації полігону одне число, яке називають числом Ейлера. Воно обчислюється за формулою:
Е = Н – (F - 1), (4.1)
де: Е – число Ейлера; Н – кількість отворів у всіх полігонах регіону; F – кількість полігонів у фрагментованому регіоні (можливі від’ємні значення (-1)). Приклади обчислення наведені на рис. 4.5.
У табл..4.1. наведені деякі конфігурації з відповідними значеннями числа Ейлера, з якої можливо побачити співвідношення параметрів, що дають однакові значення числа Ейлера. табл. 4.1. Числа Ейлера для різних комбінацій кількості отворів (Н) і фрагментів (F).
Друга група міри полігонів, які відносяться до їх границь, дуже багато- чисельна. Це міри встановлюються на основі відношення вісь, на основі тільки периметру, на основі тільки площ, на основі відношення периметру і площі тощо. Більшість цих мір пов’язано з відношенням периметру до площі і його можливо розглядати, як міру форми полігону. Однак ця міра не описує дійсну геометричну форму об’єкта. Для цього форму об’єкту необхідно порівняти з відомими геометричними фігурами: трикутник, трапеція, паралелограм. Але найбільш простою та легко визначаємою фігурою є коло. Тому основним методом вимірювання форми об’єкту є порівняння її з колом. В зв’язку з використанням кола, як фігури порівняння, ми можемо говорити, що ця міра є і мірою випуклості або вогнутості полігону. Загальна формула випуклості об’єкту у векторних геоінформаційних системах така:
СІ = к · Р/А, (4.2)
де: СІ – індекс випуклості; к – константа; Р – периметр об’єкту; А – площа. Значення константи визначається розміром кола, що може бути описане біля многокутника та приймає значення від 1 до 99. Значення 100 ми будемо мати для ідеального кола. В растровій моделі використовується така ж сама ідея, але площа об’єкту визначається, як кількість чарунок, а квадратний корінь з цього значення використовується для отримання того ж самого діапазону від 1 до 99 значень подібності. Формула визначення подібності в растрових геоінформаційних системах наступна:
СІ = де: СІ – індекс випуклості; Р – периметр; N – площа об’єкту у растровому форматі. Існує ще одна міра конфігурації границь, яка називається розвитком границі, що використовує крайовий фільтр. Фільтри, що використовуються для оцінки або зміни растрових зображень, є матрицями коефіцієнтів, які застосовуються до чарунок растру, що знаходяться у “вікні” під матрицею. Після виконання операцій з однією групою чарунок, матриця зміщується на одну чарунку і операція повторюється, що і дало назву “ковзаюче вікно”. В дистанційному зондуванні фільтри використовуються для двох основних задач – підкреслювання деталей і згладжування. Фільтри першого типу підкреслюють лінії і край областей, а фільтри другого типу – навпаки, послабляють різкі переходи між значеннями сусідніх чарунок растру. Хоча застосування таких фільтрів більш пов’язано з класифікацією областей, розглянемо їх як засіб оцінки конфігурації границь. Візьмемо вікно розміром 4 на 3 чарунки, яке накладено у двох місцях на границі області (рис. 4.6).
Кожній чарунці растру ми присвоюємо одиницю, якщо вона має той же самий атрибут, що і границя, яка нас інтересує. У випадку, коли чарунка растру має атрибути будь-якого іншого об’єкта покриття то їй присвоюємо значення нуля. Індекс границь отримується простим підрахунком кількості чарунок з одиницею, що відповідає краю об’єкта. Чим більше одиниць, тим більше внутрішньої області полігону ми маємо. І навпаки, чим менше число чарунок має значення одиниці, тим більше площі відноситься до фону. Вимірювання відстаней. Вимірювання відстаней між об’єктами важливо для аналізу відношень між об’єктами, але і також, як безпосередня оцінка наближення до них, або знаходження біля них. Тому відстань може вимірюватися просто – як фізична відстань між двома точками і, як функціональна відстань – вимірювання відстані може враховувати вартість пересування по місцевості. Проста відстань. Визначення простої відстані, відомої як евклідова відстань, відносно просто здійснюється, як в растрових так і у векторних системах. В растрових системах відстань вимірюється кількістю чарунок між точками, яка може перетворюватися в стандартні одиниці довжини множенням на величину дозвільної спроможності растру. Відстань по діагоналі визначається за теоремою Піфагора. Крім такого способу визначення відстань між точками існує і інший спосіб, при якому заздалегідь підраховується відстань від певної точки до всіх інших можливих точок покриття. В растрі це робиться створенням набору концентричних кіл з центром у заданій точці, кожна наступна з яких має радіус на одну чарунку більше. В результаті утворюється ізотропна поверхня, оскільки вона однакова за всіма напрямками (рис.4.7). У трьохвимірному просторі вона може зображатися як конус, центр основи якого знаходиться у визначеній точці.
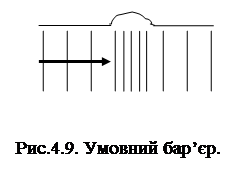
Існує модифікація цього методу, в якому відстань відмірюється не від точки, а від полігону. Це може бути відстань від межі міста. В результаті ми будемо мати карту подорожі до всіх точок покриття зовні міста від його межі. Як вже розглядалося раніше, у векторному покритті відстань між двома точками визначається за теоремою Піфагора, а загальною довжиною багато- сегментної лінії є сума довжин відрізків, які її складають. Оскільки векторні структури даних не визначають явним чином зміст простору у проміжках між введеними об’єктами, то в цих проміжках не можуть виконуватися і підрахунки. Розглянуте обмеження також відноситься і до створення ізотропнихповерхонь. Для здійснення таких підрахунків потрібна інша структура подання векторних даних, що спеціально створена для моделювання поверхні. Найбільш розповсюдженою такою структурою є розглянута нами раніше нерегулярна тріангуляційна мережа (TIN).В цій моделі можуть визначатися відстані, але з значними обчислювальними витратами. Користувачі ГІС, що працюють з моделями поверхней, частіше всього використовують растрові системи, особливо тоді, коли потрібно вимірювати відстані на поверхні. Функціональна відстань. Нашу можливість переміщуватися по прямій часто обмежують перешкоди або складна місцевість. Таким чином утворюється фрикційна поверхня. Фрикційна поверхня – це область, яка уповільнює наше переміщення, збільшуючи час досягнення визначеної точки у порівнянні з поверхнею без опору (рис.4.8). Перешкоди або бар’єри для руху на поверхні існують двох типів: абсолютні, шлях через які неможливий (скали, озера, тощо); умовні, які ідентичні фрикційним поверхням, але займають лише невеликі ділянки поверхні. Прикладами умовних перешкод є горбиста місцевість, невеликі річки, ділянки лісу, тощо. Абсолютні бар’єри зупиняють або відхилюють рух. В той же час умовні бар’єри і фрикційні поверхні накладають деяку вартість на переміщення, затримуючи його або вимагаючи більшої витрати енергії. В той же час при переміщенні по ізотропній поверхні геоінформаційна система звичайно додає одну чарунку растру на одиницю шляху і, результуюча поверхня функціональних відстаней буде подібна поверхні простих геометричних відстаней. Тепер розглянемо приклад. Перпендикулярно напрямку руху зверху донизу карти є умовний бар’єр. Ми можемо зробити його приписав пікселам в межах бар’єру значення опору, що дорівнює 5, а не 1. Тоді, переміщуючись зліва направо до бар’єру ми зустрічаємо опір у одну одиницю на кожну чарунку растру, яку проходимо. Підійшовши до бар’єру ми повинні додати у п’ять разів більше зусиль на подолання тільки однієї чарунки, що належить бар’єру, для того щоб його подолати. Такий бар’єр називається відносним (або умовним), так як він може бути подоланий за умови додаткових зусиль (рис.4.9).
Абсолютний бар’єр можливо уявити собі як де-яке продовження ідеї умовного бар’єру (рис.4.10). Для лінійного об’єкту ми просто присвоюємо йому значення, яке не можливо подолати в рамках задачі, яку вирішуємо. Хоча ідея надання значення опору чарунці растру – проста, її використання викликає складнощі. В нас частіше всього немає точних значень опору. Тому, результати аналізу відстаней з використанням бар’єрів і фрикційних поверхонь повинні розглядатися критично, особливо коли ці результати будуть використовуватися для прийняття рішень.
Окремо ми повинні розглянути дві додаткові характеристики відстані. Відстань може розглядатися як евклідова або неевклідова, ізотропна або функціональна, але і як інкрементна або наростаюча відстань. Інкрементна відстань складається з довжини етапів пройденого шляху. Кожний послідуючий етап додається як міра довжини так, як це робилося з ізотропною поверхнею. Іншими словами – інкрементна відстань – це найкоротший шлях між двома точками без урахування опору під час руху. Якщо інкрементна відстань вимірюється по всій поверхні, то ми отримаємо поверхню найкоротших відстаней. Коли ми маємо обмеження лініями або дугами, то маємо справу з лініями найкоротших відстаней, а не з поверхнею. Метою визначення функціональної відстані на поверхні з опором є пошук маршруту найменшої вартості, або найкоротшої відстані між двома точками покриття (рис.4.11). Відповідно, ми можемо побудувати і поверхню найменшої вартості для переміщення з однієї точки у всі інші точки покриття.

Для створення маршруту найменшої вартості (в протилежність найкоротшому маршруту) на растрі, починаючи з встановленої початкової чарунки шукаємо серед сусідніх чарунок таку, яка має найменше значення опору. Ця чарунка стає вихідною точкою для наступної ітерації. Процес продовжується, поки не буде досягнута потрібна точка. Таким чином ми отримаємо маршрут з вершини до потрібної точки, який потребує найменшу кількість зусиль. Хоча одного маршруту може бути достатньо, корисно розглянути всі можливі маршрути із установленого місця з урахуванням опору руху на фрикційній поверхні. В такому випадку ми будемо мати дві сітки растра. Перша – це масив значень опору, друга – обчислене значення наростаючої відстані з урахуванням опору. Процес обчислення в такому випадку буде більш складніший, ніж пошук найкоротшого маршруту. Тут програма не просто шукає найменше значення, але і обчислює значення для кожної суміжної чарунки з урахуванням, як евклідової відстані так і значення опору. За необхідності можуть обчислюватися і діагональні відстані між чарунками. Процес обчислення починається з чарунки (0;0). Для кожної сусідньої чарунки відстань вважається наростаючою на півшага множенням кожної зайнятої чарунки растру (включаючи початкову) на її значення опору і на значення її ширини (відстань по сітці: горизонтально і вертикально = 1; по діагоналі = Ö2 = 1,41). Оскільки ми пересуваємося із середини початкової чарунки до середини наступної, то перемножуємо кожну на 0,5, з метою показати наростаючу відстань у півшага. Таким чином, в загальному випадку формула для кожного кроку на половину чарунки растру наступна: 0,5 х (відстань по сітці х коефіцієнт опору). Потім ми повинні додати це до накопиченої величини опору. Наступний крок – вибір найменшої накопиченої відстані для кожної прилеглої чарунки. Потім цей процес повторюється. Значення відстані і значення опору на всіх кроках додаються разом для отримання наростаючого підсумку. В результаті ми отримаємо поверхню найменших витрат, а не один маршрут (рис. 4.12). Використовуючи ці дані є можливість визначити маршрут найменшої вартості з будь-якої і у будь-яку точки покриття. Це завдання вирішується простим перебором суміжних чарунок з найменшими значеннями вартості.
У випадку векторних координат, які описують точкові, лінійні і площинні об’єкти, для визначення відстані можуть використовуватися модифікації класичної теореми Піфагора (рис.4.13). Вихідною є формула для прямолінійної відстані між двома точками: D = Однак, у випадку, коли ми не можемо рухатися по прямій (є деякі перешкоди), то використовується неевклідова форма теореми Піфагора:
де: к – відповідний коефіцієнт від 0 до 2, що визначається в залежності від умов руху. Нескладно встановити, що коли k = 2, тоформула4.5 перетворюється у попередню.
Наприклад, ми шукаємо відстань між двома точками у місті, де будівлі і квартали обмежують наш рух відрізками під прямим кутом друг до другу. В такому випадку ми маємо значні обмеження руху, і змінна k прийме значення 1, а формула відстані (4.5) прийме вид:
Тому, люба відстань у векторній базі даних може бути визначена простою зміною значення параметра k у відповідності з умовами, які склалися. Значення k = 1,5 відповідає випадку десь між відстанню у місті та евклідовою відстанню. Крім того, фрикційні поверхні можуть оцінюватися за допомогою цієї формули. Наприклад, значення k = 0,6 дозволяє користувачу знайти найменшу відстань коло деякого бар’єру, наприклад – озера. Підсумовуючи викладений матеріал, потрібно відмітити, що з лінійними об’єктами та полігонами можливо виконувати певний перелік вимірів, які є корисними та необхідними під час виконання завдань аналізу просторової інформації за допомогою геоінформаційної системи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.068 с.) |


 (4.3)
(4.3)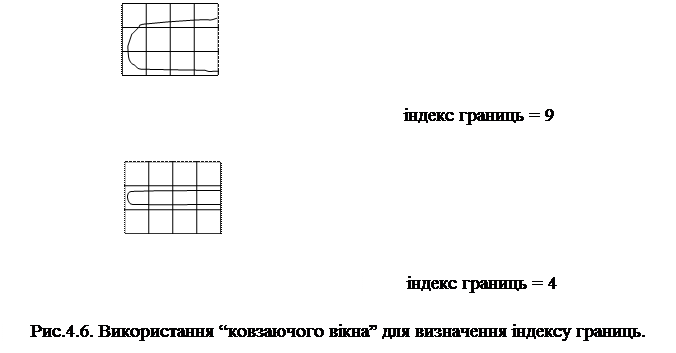 1
1

 Умовний бар’єр може бути не тільки тонкою лінією, але і площинним об’єктом. Можливі випадки, коли значення опору руху буде різним в різних чарунках растру і, більш того, значення опору в одній чарунці растру може бути різним при переміщенні через неї за різними напрямкам.
Умовний бар’єр може бути не тільки тонкою лінією, але і площинним об’єктом. Можливі випадки, коли значення опору руху буде різним в різних чарунках растру і, більш того, значення опору в одній чарунці растру може бути різним при переміщенні через неї за різними напрямкам.


 (4.4)
(4.4)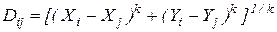 , (4.5)
, (4.5)





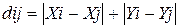 (4.6)
(4.6)


