
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подобие граничных и начальных условийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При исследовании какого-либо объекта или технологического процесса составляют систему дифф. Уравнений, которые описывают этот процесс на основе одного или нескольких физических законов. Эта система описывает процесс и устанавливает связь между пространственно-временными изменениями физических величин. Сами по себе эти физические величины характеризуют процесс в общем виде. Чтобы из системы дифф. Уравнений и целого ряда процессов выделить один конкретный, необходимо ограничить систему дифуров определенными условиями. Для ограничения нужно: - задать распределение в пространстве или в объеме важных для данного объекта знач. Факторов в начальный момент времени - задать взаимоотношения с окружающей средой на границах систем (равентсво скорости потока = 0 у стенок трубопровода). Граничные условия бывают 4 родов: I рода имеют место быть если зависимость изменения температуры задана в виде функции в интервале времени. II рода задаются тепловым потоком III рода соответствуют зависимости температуры стенки объекта от температуры среды IV рода – граничные условия задаются при модкор. Среды Подобие граничных и начальных условий соблюдается при подобии геометрических, физических и временных величин. Теоремы подобия Практическое применение теорий подобия к экспериментальному и теоретическому исследованию процессов основано на трех теоремах подобия Теорема Ньютона – Бертрана Подобные явления характеризуются численно равными критериями подобия или у подобных явлений критерии подобия равны 1. Теорема Бэкингема – Федермана Любая зависимость между физическими величинами, характеризующими явление или процесс, может быть представлена в виде взаимной зависимсти между критериями подобия. Теорема Кирпичева – Гухмана (обратная первой) Подобны те явления или системы, которые описываются одинаковыми уравнениями связи, и условия однозначности которых подобны. Теорема ОСНОВНАЯ Бэкингема (П-теорема) Первые 3 теоремы формулируют необходимость и достаточность условий для рассмотрения подобия явлений и процессов. Всякое уравнение, связывающее между собой n физических величин, среди которых m величин обладают независимыми размерностями, может быть преображено к уравнению, связывающему (n-m) безразмерных комплексов (критериев П и симплексов, состоящих из этих величин).
Лекция 4 Метод анализа размерностей и основные критерии подобия 𝜋-теорема широко используется при проведении экспериментальных исследований, так как она позволяет находить связь не между отдельными физическими величинами, а между их безразмерными соотношениями 𝜋. Каждое из этих соотношений составляется по определенному закону. Метод анализа размерностей Позволяет выражать функциональную зависимость для любого процесса в виде уравнения связи между ними. Это уравнение связи строго определяется числом безразмерных комплектов, которые состоят из физических величин со своей размерностью. Метод анализа размерностей базируется на двух допущениях: - из практических данных известно от каких параметров процесса и переменных зависит функция или рассматриваемая физическая величина - связь между всеми необходимыми для данного процесса физическими величинами выражается в виде степенного многочлена Для того чтобы использовать степенной многочлен на практике нужна степенная однородность. В уравнение подставляют размерности входящих в него величин, и тем самым достигается размерная однородность. Размерная однородность обеспечивает независимость уравнения от переменных, которые имеют каждая свою единицу измерения. Это называется инвариантностью уравнения. Пример: Рассмотрим ламинарное движение жидкости в прямой трубе. Допустим, что мы не знаем закона движения этой жидкости, но имеем ряд практических данных и можем предположить, что перепад давления в начале и в конце трубы зависит от Функция этого степенного уравнения имеет размерную однородность. Каждый член этого уравнения имеет свою единицу измерения и чтобы сделать это уравнение инвариантным мы должны привести его к инвариантному виду, поэтому
Для достижения инвариантности добавляем безразмерный постоянный коэффициент В. Размерная однородная система, которая состоит из размерных величин, может быть заменена безразмерной системой. Для этого составляется матрица величин, и мы выражаем все размерности через 3 основные (m, l, t) После всех математических преобразований уравнения мы получаем 3 основных комплекса безразмерных
Запишем уравнение в критериальной форме
Для перехода от функциональной зависимости к критериальной форме используют критерии подобия. Эти критерии применяют для описания гидравлических, механических и прочих процессов. Критерии подобия
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

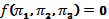

 – критерий Эйлера;
– критерий Эйлера; - критерий Рейнольдса;
- критерий Рейнольдса; - геометрический симплекс или инвариантное постоянство.
- геометрический симплекс или инвариантное постоянство.



