
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний.
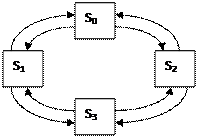
В графе состояний каждой дуге необходимо приписать интенсивность соответствующего перехода из одного состояния в другое. l - поток отказов. m - поток «окончаний ремонтов».
l1 m2
l2 l1
m2 m1
Пусть рассматривается система S, имеющая n возможных состояний S1, S2, … Sn. pi(t) – вероятность i-го состояния, вероятность того, что в момент t система будет находиться в состоянии Si.
По различному графу состояний можно найти все вероятности pi(t) как функции времени. Для этого составляются и решаются уравнения Колмогорова – особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.
Пример построения функций Колмогорова:
l21 l13 l12
l32
S – система, у которой 4 состояния S1, S2, S3, S4. Dt – малое приращение времени. Тогда p1(t+Dt)= p1(t)(1-(l12+l13) Dt)+ p2(t) l21Dt (l12+l13) Dt– вероятность выхода S за момент время Dt из S1 в S2 или S3 соответственно. Раскроем скобки, перенесем p1(t) в левую часть, разделим на Dt:
При Dt–>0 слева получаем в пределе производную: Аналогично получаем остальные дифференциальные уравнения и записываем их в систему:
Правило составления уравнений Колмогорова: В левой части каждого из уравнений Колмогорова стоит производная вероятности i-го состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного i-го состояния. Пусть t->∞. Если существует limpi(t)=pi, i= В теории случайных процессов доказывается, что, если число n состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют (это условие достаточно, но не необходимо). При t->∞ в системе S устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Финальную вероятность состояния Si можно истолковать как среднее относительное время пребывания системы в этом состоянии.
Т. к. финальные вероятности p1,p2,…, pn постоянны, то левые части уравнений Колмогорова полагаем равными нулю и решаем обычную систему алгебраических уравнений, дополнив ее нормировочным условием
Т. к. p1,p2,… постоянны, то их производные равны нулю. Поэтому:
Т. к. p1+p2+p3+p4=1, то можно решать однородное уравнение, найти финальные вероятности состояний системы, которые могут помочь оценить эффективность работы системы.
67. Схема гибели и размножения. Функциональные вероятности. Формула Литтла
Схема гибели и размножения. Мы знаем, что имея в распоряжении размеченный граф состояний, можно легко написать уравнения Колмогорова для вероятностей состояний, а также написать и решить алгебраические уравнения для финальных вероятностей. Для некоторых случаев удается последние уравнения решить заранее, в буквенном виде. В частности, это удается сделать, если граф состояний системы представляет собой так называемую «схему гибели и размножения».
Граф состояний для схемы гибели и размножения имеет вид, показанный на рис. 19.1. Особенность этого графа в том, что все состояния системы можно вытянуть в одну цепочку, в которой каждое из средних состояний (S1, S2,..., Sn-1) связано прямой и обратной стрелкой с каждым из соседних состояний — правым и левым, а крайние состояния (S0, Sn) — только с одним соседним состоянием. Термин «схема гибели и размножения» ведет начало от биологических задач, где подобной схемой описывается изменение численности популяции. Схема гибели и размножения очень часто встречается в разных задачах практики, в частности — в теории массового обслуживания, поэтому полезно, один раз и навсегда, найти для нее финальные вероятности состояний. Предположим, что все потоки событий, переводящие систему по стрелкам графа,— простейшие (для краткости будем называть и систему S и протекающий в ней процесс — простейшими). Пользуясь графом рис. 19.1, составим и решим алгебраические уравнения для финальных вероятностей состояний (их существование вытекает из того, что из каждого состояния можно перейти в каждое другое, и число состояний конечно). Для первого состояния S0 имеем:
Для второго состояния S1:
В силу (8.1) последнее равенство приводится к виду
далее, совершенно аналогично
и вообще
где k принимает все значения от 0 до n. Итак, финальные вероятности р0, p1,..., рn удовлетворяют уравнениям
кроме того, надо учесть нормировочное условие p0 + р1+ р2+…+ рn=1 (8.3) Решим эту систему уравнений. Из первого уравнения (8.2) выразим р1 через р0.
Из второго, с учетом (8.4), получим:
из третьего, с учетом (8.5),
и вообще, для любого k (от 1 до N):
Обратим внимание на формулу (8.7). В числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данного состояния Sk), а в знаменателе — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево (с начала и до Sk). Таким образом, все вероятности состояний p1, р2, …, pn выражены через одну из них (p0). Подставим эти выражения в нормировочное условие (8.3). Получим, вынося за скобку p0:
отсюда получим выражение для р0.
(скобку мы возвели в степень -1, чтобы не писать двухэтажных дробей). Все остальные вероятности выражены через р0 (см. формулы (8.4) — (8.7)). Заметим, что коэффициенты при p0 в каждой из них представляют собой не что иное, как последовательные члены ряда, стоящего после единицы в формуле (8.8). Значит, вычисляя р0, мы уже нашли все эти коэффициенты. Полученные формулы очень полезны при решении простейших задач теории массового обслуживания. Формула Литтла Рассмотрим СМО произвольного типа: одноканальная, многоканальная, с неограниченной или ограниченной очередью. С ней связаны два потока заявок, прибывающих в СМО и покидающих СМО. Если в системе установился предельный стационарный режим, то оба потока имеют одинаковую интенсивность. X(t) – число заявок, прибывших в СМО до момента t. Y(t) – число заявок, покинувших СМО до момента t. Обе функции случайны и меняются скачком (увеличиваются на 1 в моменты прихода или ухода заявок).
Пусть T – большой промежуток времени. Для него среднее число заявок, находящихся в СМО:
Интеграл равен сумме прямоугольников, высота которых равна 1, а основание равно времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена t1, t2, … Тогда
Wсист. – среднее время пребывания заявки в системе. Тогда Lсист=λWсист, и
Формула может быть использована для любой СМО (любой характер потока заявок, любое распределение времени обслуживания и дисциплины обслуживания).
Lоч – среднее число заявок в очереди. Wоч – среднее время пребывания заявки в очереди. 68. Одноканальные СМО с неограниченной очередью. Пусть потоки обслуживания и поступления заявок стационарны. λ – интенсивность поступления заявок. μ – интенсивность обслуживания заявок. Потоки λ и μ – простейшие.
Граф состояний:
S0 – канал свободен. S1 – канал занят (обслуживает заявку), очереди нет. S2 – канал занят, одна заявка в очереди. S3 – канал занят, две заявки в очереди. … Sk – канал занят, (k-1) заявок стоят в очереди.
… Теоретически число состояний ничем не ограничено (∞). Таким образом – это схема гибели и размножения с бесконечным числом состояний. Для такой системы финальные вероятности существуют не всегда (при t->∞ очередь может неограниченно возрастать), а только при r<1, когда система не перегружена.
При При Пусть
p0=1-ρ (1) p1=ρp0 p2=ρ2p0 … (2) pk=ρkp0,… Тогда, учитывая (1),
Z – случайная величина, характеризующая число заявок в системе, имеет возможные значения
Сумма быстро убывает – геометрическая прогрессия с первым членом
По формуле Литтла
Найдем среднее число заявок в очереди Число заявок в очереди равно числу заявок в системе минус число заявок, находящихся под обслуживанием. X - число заявок под обслуживанием, pk=pканала
По формуле Литтла
70. n-канальные СМО с неограниченной очередью.
…
…
Естественное условие существования финальных вероятностей Пусть
Тогда
Пусть
71. n-канальные СМО с отказами. Задача Эрланга – классическая задача ТМО, возникла из практических нужд телефонии, была решена датским математиком Эрлангом. Постановка задачи: n – количество каналов связи (линий связи), на которые поступает поток заявок с интенсивностью
…
Вычислим характеристики работы СМО. Финальные вероятности существуют
(1)и (2) называются формулами Эрланга.
Относительная пропускная способность Абсолютная пропускная способность:
Т.к.
72. Языки моделирования Языки и системы моделирования упрощают построение программ-имитаторов и проведение имитационных экспериментов за счет частичной или полной автоматизации переходов от одного уровня представления модели к другому. В этом состоит основное назначение языков моделирования, именно здесь и проявляется их главное преимущество перед универсальными алгоритмическими языками. Язык моделирования содержит абстрактные конструкции, непосредственно отражающие понятия, в которых представлена формализованная модель, или близкие концептуальному уровню описания моделируемой системы, с помощью которых четко классифицируют элементы моделируемой системы, элементы различных классов различают по характеристикам и свойствам, описываются связи между элементами системы и внешней среды, позволяющие изменять структуру модели. Язык моделирования предоставляется пользователем как часть системы моделирования. Система моделирования – это совокупность языковых и программных средств, которая включает: • собственно язык моделирования; • язык управления системой моделирования– язык команд интерактивного взаимодействия с пользователем; • управляющая программа – программные средства, обеспечивающие трансляцию модели и другие стандартные функции системы моделирования (продвижение модельного времени, генерацию случайных чисел, сбор статистической информации, вывод результатов и т. д.). Системы моделирования проблемно-ориентированные включают также средства разработки языков конечного пользователя. Среди большого числа языков моделирования довольно сложно выделить какое-то базовое подмножество языков, покрывающих основные потребности пользователей в средствах автоматизации моделирования. На практике существует проблема выбора системы моделирования, подходящей для поставленной задачи.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1009; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.184 (0.088 с.) |
 m1 l2
m1 l2 t
t 







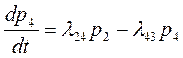
 и все пределы не зависят от начального состояния системы. Тогда они называются финальными вероятностями состояний.
и все пределы не зависят от начального состояния системы. Тогда они называются финальными вероятностями состояний. .
.





 (8.1)
(8.1)



 (8.2)
(8.2) (8.4)
(8.4) (8.5)
(8.5) (8.6)
(8.6) (8.7)
(8.7)
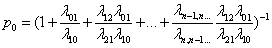 (8. 8)
(8. 8) Z(t)=X(t)-Y(t) – число заявок, находящихся в СМО.
Z(t)=X(t)-Y(t) – число заявок, находящихся в СМО.
 (1) |:T
(1) |:T

 - среднее число заявок, пришедших за время T.
- среднее число заявок, пришедших за время T. - формула Литтла (первая формула).
- формула Литтла (первая формула). - вторая формула Литтла
- вторая формула Литтла


 <1 ряд сходится.
<1 ряд сходится.
 Следовательно,
Следовательно,
 , …,
, …, ,…. Самое вероятное число заявок = 0.
,…. Самое вероятное число заявок = 0. с вероятностями
с вероятностями 
 (нулевой член = 0) – среднее число заявок в системе, выраженное через математическое ожидание
(нулевой член = 0) – среднее число заявок в системе, выраженное через математическое ожидание
 .
.  ,
, 



 По правилу сложения математических ожиданий, среднее число заявок в очереди минус (среднее число заявок под обслуживанием)
По правилу сложения математических ожиданий, среднее число заявок в очереди минус (среднее число заявок под обслуживанием)  .
.
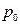 k=p0, вероятность того, что канал свободен
k=p0, вероятность того, что канал свободен
 , вероятность того, что канал занят
, вероятность того, что канал занят
 - средне число заявок под обслуживанием.
- средне число заявок под обслуживанием.

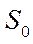 - в СМО нет ни одной заявки
- в СМО нет ни одной заявки - в СМО находится 1 заявка (один канал занят, остальные свободны)
- в СМО находится 1 заявка (один канал занят, остальные свободны) -
-  - // - занято, очереди нет
- // - занято, очереди нет - 1 заявка в очереди
- 1 заявка в очереди - в очереди
- в очереди  заявок
заявок
 . Если
. Если  , очередь растет до бесконечности.
, очередь растет до бесконечности.
 - бесконечно убывающая геометрическая прогрессия
- бесконечно убывающая геометрическая прогрессия ,
,  ,
, 


 -среднее число занятых каналов
-среднее число занятых каналов - среднее число заявок в очереди
- среднее число заявок в очереди , тогда
, тогда 
 - бесконечно убывающая геометрическая прогрессия.
- бесконечно убывающая геометрическая прогрессия. ,
,  ,
, 


 ,
,  ,
, 
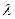 . Поток обслуживаний имеет интенсивность
. Поток обслуживаний имеет интенсивность  . Потоки простейшие. Граф состояний соответствует схеме гибели и размножения.
. Потоки простейшие. Граф состояний соответствует схеме гибели и размножения.
 - в СМО нет ни одной заявки
- в СМО нет ни одной заявки - в СМО находится 1 заявка (один канал занят, остальные свободны)
- в СМО находится 1 заявка (один канал занят, остальные свободны) - - // -
- - // -  - // - (
- // - (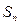 - - // -
- - // -  чтобы из
чтобы из 
 чтобы из
чтобы из  перейти в
перейти в  ).
).
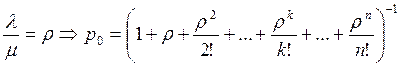 (1)
(1) ,
,  , …,
, …,  , …,
, …, 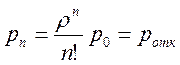 (2)
(2)
 .
. .
. - среднее число занятых каналов.
- среднее число занятых каналов.
 - абсолютная пропускная способность не что иное, как интенсивность потока обслуженных заявок, следовательно, каждый занятый канал обслуживает в единицу времени
- абсолютная пропускная способность не что иное, как интенсивность потока обслуженных заявок, следовательно, каждый занятый канал обслуживает в единицу времени 



