
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка степени согласованности порядковых показателей
Расстояние d (R ( X ), R ( Y )), определяемое согласно (37), можно использовать в качестве меры близости не только для отношений порядка или эквивалентности, но и для любых бинарных отношений R ( X ) и R ( Y ). Однако в прикладных задачах квалиметрии чаще всего рассматриваются именно отношения порядка, соответствующие оценкам показателей, измеряемым по ординальной шкале. При этом нередко интерес представляет оценка степени согласованности порядковых показателей, позволяющая судить о том, насколько зависимы эти показатели между собой и, следовательно, возможен ли прогноз значений одного показателя на основе значений другого. Для этих целей наиболее часто используются меры связи, аналогичные известному из теории вероятностей коэффициенту корреляции. Напомним, что коэффициент (парной) корреляции r (X, Y) для числовых случайных переменных X и Y определяется следующим выражением: r (X, Y) =
где M (X), M (Y), M (XY) – соответственно средние значения (математические ожидания) величин X, Y и произведения XY; D (X), D (Y) – соответственно дисперсии величин X и Y. Кроме того, если имеется выборка из n объектов, каждый из которых характеризуется показателями X и Y, и если пара чисел (xi, yi) обозначает полученные в результате наблюдений (оценок, измерений) значения этих показателей для i –го объекта (i = 1,…, n), то выборочная оценка
где Коэффициент корреляции (48), как известно, обладает следующими основными свойствами: 1) –1 £ r (X, Y) £ 1, причем равенство достигается, если между показателями X и Y существует линейная зависимость вида Y = a X + b. В этом случае при a < 0 r (X, Y) = –1 а при a > 0 r (X, Y) = 1. 2) если показатели X и Y статистически независимы, то r (X, Y) = 0. Для показателей, измеряемых по ординальной шкале, можно построить меры связи, обладающие аналогичными свойствами. Коэффициент ранговой корреляции Спирмена. Пусть на основе результатов оценки n объектов по двум порядковым показателям X и Y получены две ранжировки:
R 1(X), R 2(X), …, Rn- 1(X), Rn (X) R 1 (Y), R 2(Y), …, Rn- 1(Y), Rn (Y). (50)
Вначале рассмотрим случай, когда связные ранги отсутствуют, т.е. когда степени проявления качества по обоим показателям у всех объектов различимы и, следовательно, никакие два объекта не оценены как эквивалентные. Это допущение означает, что обе строки в матрице (50) представляют собой перестановки первых n натуральных чисел { 1,…, n }.
Чем более согласованы между собой две данные ранжировки, тем меньше должны различаться соответствующие элементы первой и второй строк матрицы (2.50). В качестве меры согласованности вполне естественно взять функцию от суммы S квадратов разностей рангов, полученных объектамипо X и по Y:
S =
Ясно, что если обе ранжировки полностью совпадают, то есть если для всех i = 1, …, n будет Ri ( X ) = Ri ( Y ), то сумма (51) принимает свое минимальное значение, равное нулю. Пронумеруем все n объектов в порядке снижения их качества по показателю X: от самого лучшего к самому худшему. Заметим, что мы вправе выбрать любую нумерацию объектов, так как наши выводы, разумеется, не должны зависеть от нумерации. Поэтому далее там, где это удобно, будем считать, что объекты расположены именно в таком порядке. В этом случае, очевидно, будет выполняться условие
Ri ( X ) = i, (i = 1,…, n),
и тогда матрица (50) приобретет следующий вид:
R 1(Y), R 2(Y), R3 (Y), …, Rn- 1(Y), Rn (Y). (52)
Потребуем, чтобы коэффициент, характеризующий степень согласованности двух ранжировок, который далее будем обозначать ρ, линейно зависел от суммы S, определяемой согласно (51):
ρ = a S + b, (53)
(a и b – числовые коэффициенты, которые следует определить) и лежал в пределах: –1 ≤ ρ ≤ 1. Кроме того, потребуем, чтобы случай ρ = 1 означал бы полное совпадение двух ранжировок, а случай ρ = –1 их полную “противоположность”, т.е. случай, когда объект, наилучший по показателю X, являлся бы наихудшим по показателю Y и т. д. В этом “крайнем“ случае матрица (52) имела бы следующий вид:
n, n –1, n –2, …, 2, 1, (54)
т.е. Ri ( Y ) = n +1 – i (55)
В этом случае сумма (51), как легко видеть из (55), будет равна
S = (n –1)2 + (n –3)2 + …+ [2 – (n –1)]2 + (1– n)2 = = 2(n –1)2 + 2(n –3)2 + … =
= (56) 2
С учетом известного соотношения для суммы квадратов первых k чисел натурального ряда:
из (56) можно легко получить, что в случае «противоположных» ранжировок (54) сумма S принимает свое максимально возможное значение S =
Теперь, возвращаясь к условию (53), можем определить неизвестные коэффициенты a и b:
1 при S = 0 ρ = a S + b = (59) – 1 при S = n (n 2 –1) ] / 3.
Решив (59) как систему двух уравнений относительно неизвестных a и b, находим в итоге явный вид коэффициента ρ
ρ = 1 –
который называют ранговым коэффициентом корреляции Спирмена по имени известного британского психолога, впервые предложившего использовать этот коэффициент. При выводе формулы (60) предполагалось, что все ранги в каждой из двух ранжировок различны (отсутствие связных рангов использовалось, в частности, в условии (58)). Если же хотя бы в одной ранжировке имеются связные ранги, то формула (60) перестает быть эффективной, и ее применение даже может исказить результат. Для иллюстрации этого обстоятельства можно рассмотреть тот крайний случай, когда по показателю Y качество всех n объектов одинаково. Тогда, используя (24), нетрудно заметить, что ранжировки (56) будут иметь вид
½ (n +1), ½ (n +1),.…, ½ (n +1).
Несложный подсчет по формуле (60) дает для этих данных значение ρ = 0,5. В то же время логика подсказывает, что в данном случае между ранжировками нет никакой, в частности, положительной, корреляции. В силу этого обстоятельства рекомендуется при наличии связных рангов вычислять ранговый коэффициент корреляции Спирмена, применяя к рангам (50) общую формулу (49) вычисления парного коэффициента корреляции. Для этого в качестве элементов векторов (х 1,.., х n) и (у 1,.., у n) следует взять ранжировки соответственно по X и по Y: х 1 = R 1(X),..., х n = R n(X); y 1 = R 1(Y),..., y n = R n(Y), (61) и применить к этим данным формулу (49). Обоснованием такого метода вычисления ρ служит следующее утверждение. Если в обеих ранжировках отсутствуют связные ранги, то вычисление рангового коэффициента корреляции Спирмена ρ по формуле (60) и применение формулы (49) к ранжировкам (61) дают одинаковый результат.
Ранговый коэффициент корреляции Спирмена может использоваться, например, в качестве критерия проверки гипотезы о наличии или отсутствии согласованности мнений двух экспертов. При этом сами по себе понятия «отсутствие согласованности» или «независимость мнений экспертов» нуждаются в уточнении. Чаще всего эти понятия принято моделировать следующим образом. При любой заданной ранжировке R ( X ), полученной от первого эксперта, все ранжировки
(R 1(Y), R 2(Y), …, Rn- 1(Y), Rn (Y)), (62)
полученные от второго эксперта, считаются равновероятными. Каждая из ранжировок (62) представляет собой перестановку первых n чисел натурального ряда. Всего имеется n! таких перестановок. Следовательно, если гипотеза об отсутствии согласованности мнений экспертов верна, то вероятность каждой из ранжировок (62) следует принять равной (n!)−1. Для каждой из n! возможных ранжировок (62) может быть подсчитан ранговый коэффициент корреляции ρ. Таким образом, за счет допущения о равновозможности любых сочетаний результатов, полученных от первого и от второго экспертов, мы приходим к тому, что сам ранговый коэффициент корреляции Спирмена становится случайной величиной, которая принимает каждое из n! своих значений (не все из этих значений обязательно будут различны) с вероятностью, равной (n!)−1.
Такой прием, когда разброс значений представляющего интерес параметра (в данном случае – ρ) описывается с помощью того или иного закона распределения вероятностей (в данном случае – равномерного) носит название рандомизация. Можно показать, что математическое ожидание и дисперсия величины ρ будут равны, соответственно, M (ρ) = 0, D (ρ) = (n -1)−1. Подчеркнем, что это справедливо, только если верна высказанная выше гипотеза о независимости ранжировок, так как именно ей соответствует модель равной вероятности каждой из ранжировок (62).
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.127.197 (0.023 с.) |
 , (48)
, (48) коэффициента корреляции r (X, Y) вычисляется по формуле
коэффициента корреляции r (X, Y) вычисляется по формуле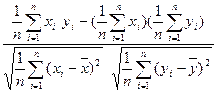 , (49)
, (49) ,
,  - выборочные средние значения X и Y, которые, как известно, являются несмещенными оценками математических ожиданий M (X)и M (Y).
- выборочные средние значения X и Y, которые, как известно, являются несмещенными оценками математических ожиданий M (X)и M (Y).
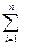 (Ri ( X ) – Ri ( Y ))2 . (51)
(Ri ( X ) – Ri ( Y ))2 . (51) 1, 2, 3, …, n -1, n
1, 2, 3, …, n -1, n 1, 2, 3, …, n –1, n
1, 2, 3, …, n –1, n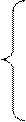 2
2  (2j)2, если n – нечетное (n = 2 k +1),
(2j)2, если n – нечетное (n = 2 k +1), , (57)
, (57)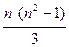 . (58)
. (58)
 , (60)
, (60) 1, 2, …., n
1, 2, …., n


