Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 7 Математические пакеты в моделировании
Виды математических программных сред. Общая характеристика программ МаMaple, MathCad, MatLab, Mathematika. Их применение в моделировании Литература[7 c. 50-250], методические рекомендации по выполнению задач домашней контрольной работы. Вопросы для самоконтроля: 1 Редактирование документов в программе MathCad. 2 Вычисление в пределах экрана (Calculate) 3 Работа с символьным процессором 4 Решение уравнения относительно заданной переменной (Solve) 5 Транспонирование матрицы (Transpose), обращение матриц (Invert)
М етодические рекомендации по выполнению задач домашней контрольной работы Методические рекомендации к решению задач графическим способом (101–115)
Графическое решение задач с двумя и n переменными рассмотрим на примерах. Пример. Решить задачу линейного программирования
графическим способом. Решение: для построения области допустимых решений строим в системе х10х2 соответствующие данным ограничениям-неравенствам граничные прямые:
х1 + х2 = 6, х1 + 4 · х2 = 4, 2 · х1 – х2 = 0.
Находим полуплоскости, в которых выполняются данные неравенства. Для этого вследствие выпуклости любой полуплоскости достаточно взять произвольную точку, через которую не проходит соответствующая граничная прямая, и проверить, удовлетворяет ли эта пробная точка ограничению-неравенству. Если удовлетворяет, то данное неравенство выполняется в полуплоскости, содержащей пробную точку. В противном случае берется полуплоскость, не содержащая пробной точки. В качестве пробной точки часто удобно брать начало координат О (0; 0). Для нашего примера область допустимых решений – множество точек четырехугольника АВСD (рисунок 1). Строим вектор с = (с1; с2) = (2; 3). Так как он необходим для выяснения направления возрастания целевой функции, иногда для большей наглядности удобно строить вектор λс (λ>0). Перпендикулярно к вектору с проводим линию уровня F = 0. Параллельным перемещением прямой F = 0 находим крайнюю точку В, в которой целевая функция достигает максимума, и точку А, в которой достигается минимум. Координаты точки В определяются системой
откуда В (2; 4), Fmax = F(B) = 16. Точку минимума А находим, решая систему уравнений граничных прямых:
Имеем А(4/9; 8/9), Fmin = F(A) = 32/9.
Рисунок 1 – Решение задачи
Пример. Найти
при ограничениях:
Решение: в данном примере n = 5, m = 3. Так как n – m = 5 – 3 = 2, то задачу можно решить графически. Решим систему ограничительных уравнений относительно любых трех неизвестных. В данном случае лучше решить систему относительно х3, х4 и х5:
Подставив выражения для х3, х4 и х5 в целевую функцию, после упрощения получим F = -2х1 – 3х2. Задача линейного программирования с двумя переменными принимает вид:
На рисунке 2 представлен многоугольник решений АВСD, линия уровня F и вектор с = (2; 3).
Максимального значения целевая функция достигает в точке А(0; 4), то есть Fmax = f(A) = -12, а минимального в точке В (6; 8): Fmin = f(В) = -36. подставив координаты точек А и В в выражения для х3, х4, х5, найдем остальные координаты экстремальных точек: А´ (0; 4; 16; 0; 0), В´ (6; 8; 0; 28). При этом Fmax = -12, Fmin = -36. Методические рекомендации к решению задач симплекс методом
Для случая большого числа переменных используется симплекс-метод, который гласит, что если задача линейного программирования имеет решение, то хотя бы одно из них – базисное. Решение задачи симплекс-методом рассмотрим на примере. Пример. Решить задачу симплекс-методом. Предприятие выпускает три вида продукции:I, II, III. Для производства продукции оно располагает ресурсами в следующих объемах (единиц): - Комплектующие изделия – 3120; - Сырьё – 3000; - Материалы – 3150. Расход ресурсов на единицу продукции каждого вида приведен ниже:
Прибыль от единицы продукции I вида составляет 240 млн руб., II – 210 млн. руб. и III – 180 млн руб. Требуется определить производственную программу предприятия, обеспечивающую максимальную прибыль. Решение: составим математическую модель задачи. Обозначим через х1, х2, х3 искомые объемы производства продукции, а через F – прибыль от производства и реализации всей продукции, которая с учетом обозначений определяется следующей функцией:
Запишем ограничения по ресурсам:
Объемы производства продукции не могут быть отрицательными, поэтому х1, х2, х3 ≥ 0. Приведем ограничения задачи к каноническому виду, добавив к их левым частям соответствующие положительные неизвестные у1, у2, у3. В результате ограничения запишутся в виде равенств:
Дополнительные неизвестные у1, у2, у3 будут базисными, так как им соответствуют единичные векторы, которые образуют базис в трехмерном пространстве. Разрешив систему относительно базисных неизвестных, получим:
Занесем условия задачи в симплексную таблицу 1:
Таблица 1 – Условия задачи
Базисное решение задачи в таблице 1 следующие: х1 = х2 = х3=0 (как небазисные неизвестные), т.е. предприятие продукции не выпускает. Тогда у1 =3120, у2 =3000, у3 = 3150. Игреки означают количество неиспользуемых ресурсов. Значит, если продукция не выпускается, то ресурсы не используются, и прибыль при этом равна нулю (F = 0). Решение задачи опорное, так как базисные неизвестные принимают положительные значения. Переходим к поиску оптимального решения. В строке функции наибольший по абсолютной величине (среди отрицательных) элемент находится в первом столбце, поэтому этот столбец берем за разрешающий и выделяем его. Разрешающую строку находим по наименьшему симплексному отношению:
Наименьшее симплексное отношение соответствует третьей строке, следовательно, она будет разрешающей, выделим ее. Выделим в таблице и разрешающий элемент, который находится на пересечении разрешающих строки и столбца. Разрешающий столбец выделен первый, так как от единицы продукции первого вида самая высокая прибыль – 240 млн. руб. Симплексное отношение означает возможные объемы производства продукции первого вида из имеющихся ресурсов, а наименьшее симплексное отношение означает максимально возможный выпуск этой продукции. В самом деле, третий ресурс позволяет изготавливать лишь 525 ед. продукции, в то время как первый ресурс – 780, а второй – 1500. Рассчитаем элементы новой симплексной таблицы 2.
Таблица 2 – Симплексная таблица
Выпишем решение из таблицы 2:
х1 = 525, х2 = х3 = 0, у1 =1020, у2 =1950, у3 = 0, F = 126000 (млн руб).
Это означает следующее: предприятие может изготовить продукции первого вида в объеме 525 ед., при этом оно получит прибыль в размере 126000 млн руб., третий ресурс будет использован полностью (у3 = 0), а первый и второй ресурсы не используются в объемах 1020 и 1950 ед. соответственно. Решение в таблице 2 не является оптимальным, так как в строке функции имеется отрицательный элемент -20. В соответствии с алгоритмом выберем разрешающий элемент (16/3) и осуществим еще одно симплексное преобразование. В таблице 3 получено оптимальное решение:
х1 = 397,5; х2 = 0; х3 = 191,25; у1 =у3 = 0, у2 =292,5.
Fmax = 129825 (млн руб).
Таблица 3 – Оптимальное решение
Из решения видно, что продукция третьего вида с самой малой прибылью (180 млн руб.) вошла в оптимальное решение задачи. Это произошло потому, что у этого вида продукции низкая норма расхода третьего ресурса. Поэтому оптимальное сочетание выпуска продукции первого и третьего вида позволило увеличить прибыль по сравнению с предыдущим решением на 3825 млн руб.
Методические рекомендации к решению двойственных задач (116–140)
Пример. Сформулировать правила построения модели любой из задач данной пары, если другая модель известна. В “а” и “б” построены пары симметричных взаимно двойственных задач. В “в” приведен порядок построения двойственной задачи к несимметричной задачи линейного программирования:
прямая задача двойственная задача а)
б)
в) пусть имеется задача линейного программирования в произвольной несимметричной форме. Построить ей двойственную:
Прежде всего ограничения типа ≥ умножением на –1 сведем к ограничениям типа ≤. Получим:
Решение. Для построения двойственной задачи необходимо пользоваться следующими правилами: 1) если прямая задача решается на максимум, то двойственная – на минимум, и наоборот; 2) в задаче на максимум ограничения-неравенства имеют смысл ≤, а в задаче минимизации – смысл ≥; 3) каждому ограничению прямой задачи соответствует переменная двойственной задачи, и наоборот, каждому ограничению двойственной задачи соответствует переменная прямой задачи; 4) матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием; 5) свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи, и наоборот; 6) если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, если же нет, то как ограничение-равенство; 7) если какое-либо ограничение прямой задачи записано как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается. В результате применения указанных правил получим следующую модель двойственной задачи для модели задачи линейного программирования, сформулированной в пункте “в”:
Методические рекомендации к решению транспортных задач
(141–197)
Пример. Построить исходный опорный план транспортной задачи, условие которой представлено в таблице 4, по правилу «северо-западного угла».
Таблица 4 – Условие задачи
Решение. В клетку (1; 1) вписываем число х11 = min (50, 40) = 40 ед. В данном случае потребность потребителя В1 полностью удовлетворяется запасом поставщика А1. Первый столбец в дальнейшем в расчет не принимается. Потребность потребителя В2 за счет поставщика А1 можно удовлетворить только частично. В клетку (1; 2) вписываем число х12 = =min (50 – 40, 60) = min (10, 60) = 10 ед. В результате такого распределения запас груза поставщика А1 полностью исчерпан, т. е. первая строка таблицы в дальнейшем в расчет не принимается. Поскольку потребность потребителя В2 удовлетворена за счет поставщика А1 частично, переходим к распределению запаса груза поставщика А2. В клетку (2; 2) вписываем число х22 = min (70, 60 – 10) = min (70, 50) = 50 ед. В этом случае потребность потребителя В2 полностью удовлетворена, а у поставщика А2 осталось 20 ед. груза. Потребность потребителя В3 за счет поставщика А2 можно удовлетворить частично (на 20 ед.). В клетку (2; 3) вписываем число х23 = min (20, 50) = 20 ед. В этом случае запас груза поставщика А2 полностью исчерпан и переходим к распределению запаса груза поставщика А3. В клетку (3; 3) вписываем число х33 = min (100, 50 – 20) = min (100, 30) = 30 ед. В результате потребность потребителя В3 полностью удовлетворена, у поставщика А3 осталось 70 ед. груза. Потребность потребителя В4 составляет 70 ед., а у поставщика А3 осталось 70 ед. груза. В клетку (3; 4) вписываем число x34 = 70 ед. Окончательно получаем таблицу 5.
Таблица 5 – Итоговая таблица
Исходным опорным планом перевозок является
Этому плану соответствует значение целевой функции
F = 4 · 40 + 3 · 10 + 4 · 50 + 5 · 20 + 7 · 30 + 5 · 70 = 1050.
Пример. Составить исходный опорный план транспортной задачи, условие которой представлено в таблице 6, по правилу «минимального элемента».
Таблица 6 – Условие задачи
Решение. Загрузка начинается с клетки, которой соответствует наименьший тариф сij из всей матрицы тарифов. Такой клеткой является (2; 4), с24 = 1. В клетку (2; 4) вписываем число х24= min (70, 70) = 70 и исключаем из дальнейшего рассмотрения вторую строку и четвертый столбец. Из оставшихся тарифов наименьшим является с13 = 2. В клетку (1; 3) вписываем число х13 = min (50, 50) = 50. В этом случае из дальнейшего рассмотрения исключаются первая строка и третий столбец. В расчет принимается распределение груза поставщика А3. В третьей строке имеем наименьший тариф для клетки (3; 1), с31 = 3. В клетку (3; 1) вписываем число x31 = min (100, 40) = 40. Оставшееся количество единиц груза от поставщика А3 помещаем в клетку (3; 2), х32 = min (100 - 40, 60) = (60, 60) = 60. Окончательно получаем таблицу 7.
Таблица 7 – Итоговая таблица
В результате полного распределения грузов получаем исходное опорное решение
для которого F = 2 x 50 + 1 x 70 + 3 x 40 + 6 x 60 = 650 ден.ед.
Очевидно, что для данного опорного плана не выполняется условие m + n – l = 3 + 4 – l = 6. План Х вырожденный.
Пример. Составить методом Фогеля опорный план ТЗ, условие которой представлено в таблице 8.
Таблица 8 – Условие задачи
Решение. По каждой строке и каждому столбцу определяем разность между двумя наименьшими тарифами и из всех разностей выбираем наибольшую. Такой разностью на первом этапе является с34 – с24 = 5 – 1 = 4 для четвертого столбца. В клетку (2; 4) вписываем число x24 = min (70, 70) = 70. Остаток груза по второй строке равен нулю, и потребность в грузе по четвертому столбцу равна нулю, а это значит, что на втором этапе вторая строка и четвертый столбец в расчет приниматься не будут. На втором этапе наибольшей разностью будет с33 – с13 = 7–2 = 5 в третьем столбце. В клетку (1; 3) вписываем число x13 = min (50, 50) = 50. На данном этапе остатки груза по первой строке и третьему столбцу равны нулю, т. е. первая строка и третий столбец на следующем этапе в расчет не принимаются. Остались одна строка и два столбца. В этом случае запас груза поставщика А3 распределяем по третьей строке для полного удовлетворения спроса потребителей B1, B2. Последовательность поставок груза в соответствующую клетку на каждом этапе можно отмечать числом в нижнем правом углу клетки. Проделав несколько таких этапов, получим опорный план перевозок, который близок к оптимальному, а иногда совпадает с ним (таблица 9).
Таблица 9 – Итоговая таблица
Полученный опорный план задачи можно представить в виде
Для этого плана транспортные издержки F=2x50+1x70+3x40+6x60=650 ден. ед. План Х вырожденный. Пример. Найти оптимальный опорный план перевозок топлива из хранилищ А1, А2, А3, в которых имеется в наличии соответственно 300, 150, 200 т топлива, предназначенного для пяти АЗС: В1, В2, В3, В4, В5. Потребности в топливе составляют соответственно 80, 170, 150, 160 и 70 т при следующей матрице затрат на перевозку 1 т топлива:
Решение. Опорное решение найдем, например, по правилу «минимального элемента» (таблица 10)
Таблица 10 – Опорное решение найденное по правилу «минимального элемента»
В таблице распределения получен вырожденный план. Условие для базисных клеток m + n – l = 3 + 5 – l = 7 не выполняется. В одну из свободных клеток (как правило, в клетку с наименьшим тарифом) вписываем число нуль (нуль-загрузка), и такая клетка считается базисной. Очень важно, чтобы из базисных клеток не образовался замкнутый цикл. Например, впишем число нуль в клетку (2;5), х25 = 0.
Построение оптимального плана перевозок методом потенциалов. Дл я определения оптимального плана перевозок необходимо построить начальный опорный план по одному из выше приведенных правил («северо–западного угла», «минимального элемента», и т.д.) Затем определяем потенциалы поставщиков. Для определения потенциалов поставщиков и потребителей имеем систему уравнений:
Поскольку число уравнений системы на единицу меньше числа потенциалов (система неопределенная), для ее решения одному из потенциалов придается произвольное значение. Положим u1 = 0. все остальные потенциалы определяются однозначно: u2 = 1, u3 = 4, v1=4, v2 = 2, v3 = 1, v4 = 0, v5 = 4. Найденные потенциалы поставщиков и потребителей указаны справа и внизу в клетках таблицы 10. Расчет их можно произвести непосредственно в таблице. Определяем оценки свободных клеток:
s12 = 7 – (0 + 1) = 6, s14 = 5 – 0 = 5, s21 = 6 – (1 + 4) = 1, s22 = 2 – (1 + 2) = -1, s23 = 4 – (1 + 1) = 2, s31 = 5 – (4 + 1) = -3, s33 = 7 – (4 + 1) = 2, s35 = 8 – (4 + 2) = 2.
Полученный план неоптимален. Среди оценок имеются отрицательные. Наиболее потенциальной клеткой является клетка (3;1). Строим замкнутый цикл для клетки (3;1). В таблице он выделен штриховой линией. В отрицательных вершинах цикла наименьшее количество груза равно min (80, 0, 30) = 0, т.е. число нуль нужно поместить в клетку (3;3), х33 = 0. Получаем новый план перевозок, хотя значение целевой функции и не изменится (таблица 11): u1 = 0, u2 = -2, u3 = 1, v1=4, v2 = 5, v3 = 1, v4 = 3, v5 = 2.
Таблица 11 – Новый план перевозок
Оценки свободных клеток следующие:
s12 = 7 – (5 + 0) = 2, s14 = 5 – (3 + 0) = 2, s21 = 6 – (-2 + 4) = 4, s22 = 2 – (-2 + 5) = -1, s23 = 4 – (-2 + 1) = 5, s31 = 3 – (-2 + 2) = 3, s33 = 7 – (1 + 1) = 5, s35 = 8 – (1 + 2) = 5.
Поскольку имеется оптимальная оценка, то план перевозок еще неоптимален и его можно улучшить за счет загрузки клетки (2;2). Строим замкнутый цикл, который включает клетки (2;2), (2;4), (3;4), (3;2). Наименьшее количество единиц груза в отрицательных вершинах цикла равно min (150, 170) = 150 ед. После смещения по циклу 150 ед. груза получим новый план (таблица 12)
Таблица 12 – Новый план перевозок
Потенциалы поставщиков и потребителей для плана, представленного в таблице 12, определены непосредственно в таблице. Оценки свободных клеток следующие:
s12 = 7 – (5 + 0) = 2, s14 = 5 – (3 + 0) = 2, s21 = 6 – (-3 + 4) = 5, s22 = 4 – (-3 + 1) = 6, s23 = 1 – (-3 + 3) = 1, s31 = 3 – (-3 + 2) = 4, s33 = 7 – (1 + 1) = 5, s35 = 8 – (1 + 2) = 5.
Все оценки свободных клеток положительны. Представленный в таблице 12 план перевозок оптимален, а так как среди оценок нет нулевых, то оптимальный план является и единственным:
Для этого плана значение целевой функции
F(Х*) = 4 · 80 + 1 · 150 + 2 · 70 + 6 · 20 + 4 ∙ 180 = 1750
Методические рекомендации к решению задач заданных с помощью графовых моделей (198–227)
Имеется несколько способов задания графа. Во многих случаях граф удобно задавать в виде матрицы смежности вершин, матрицы смежности дуг или матрицы инцидентности. Матрицей смежности вершин орграфа называется квадратная матрица А, каждый ij -ый элемент которой численно равен количеству дуг, идущих из вершины Еi в вершину Еj. Если G=(E,
Рисунок 3 – Изображение ориентированного графа
Матрица смежности вершин графа (рисунка 3) представлена в таблице 13.
Таблица 13 – Матрица смежности вершин графа
Матрицей смежности дуг (ребер) орграфа (графа) называется квадратная матрица А, каждый ij -ый элемент которой равен единице, если конечная вершина дуги
Таблица 14 – Матрица смежности ребер
Матрицей инцидентности орграфа называется прямоугольная матрица А, строки которой соответствуют вершинам, столбцы – дугам, а элементы равны 1, -1 или 0. При этом на пересечении вершины Е и дуги Если G – неориентированный граф, то можно использовать значения ε = 0, ε = 1.
Методические рекомендации к решению задач о максимальном потоке (228–257)
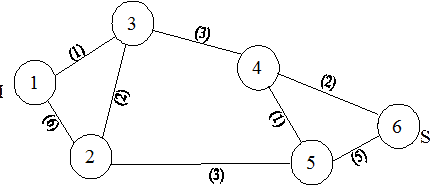
Для решения задачи необходимо рассмотреть алгоритм построения максимального потока: 1 построить некоторый начальный поток Х0 ={ х0ij }; 2 организовать процедуру составления подмножества А вершин, достижимых из истока I по ненасыщенным ребрам. Если в этом процессе сток S не попадет в подмножество А, то построенный поток максимальный и задача решена. Если же S попал в А, то перейти к п.3 алгоритма; 3 выделить путь из I в S, состоящий из ненасыщенных ребер, и увеличить поток хij по каждому ребру этого пути на Δ = min(rij - хij), где минимум берется по ребрам (i, j) упомянутого пути. Тем самым будет построен новый поток Х1 ={ х1ij }. После этого надо возвратиться к п.2 алгоритма. Применение алгоритма рассмотрим на примере. Пример. На сети, изображенной на рисунке 4, сформировать поток максимальной мощности, направленный из истока I в сток S, при условии, что пропускные способности ребер в обоих направлениях одинаковы. Выписать ребра, образующие на сети разрез минимальной пропускной способности.
Рисунок 4 - Сеть Решение. В соответствии с п.1 алгоритма на сети необходимо сформировать начальный поток Х0. Сделаем это, следующим образом. По пути 1–3–4–6 пропустим 1 ед., по пути 1–2–3–4–6 — 1 ед., по пути 1–2–5–6 — 3 ед. В результате потоки хij по ребрам сети будут равны: х12 =4, х13 =1, х23 =1, х25 = 3, х34 = 2, х46 = 2, х56 = 3; потоки по остальным ребрам сети равны нулю. Совокупность перечисленных потоков по ребрам и составит поток Х0 по сети. Видно, что условия (2) и (3), налагаемые на потоки по ребрам сети выполняются. Матрица пропускных способностей ребер данной сети приведена в таблице 15, а матрица построенного потока – в таблице 16.
Таблица 15 – Матрица пропускных способностей ребер
Таблица 16 – Матрица построенного потока
Приступая к выполнению п.2 алгоритма, составим матрицу R – Х0 (таблица 17), элементы rij – хij которой позволяют судить о ненасыщенности ребер сети. Насыщенным ребрам будут соответствовать нулевые элементы, а ненасыщенным – ненулевые. Так, ребро (1, 2) ненасыщенное, поэтому элемент r12 - х012 = 6-4=2≠0, а вот ребро (2,5) насыщенное, поэтому r25 - х025 = 3 – 3 = 0.
Таблица 17 – Матрица R – Х0
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.12.240 (0.151 с.) |
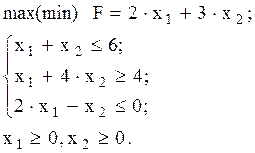
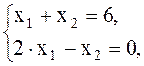






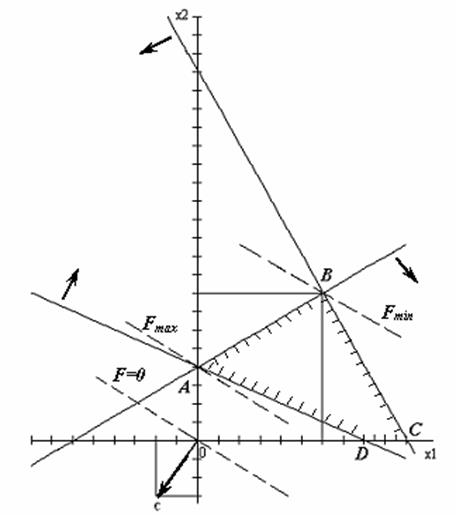
 Рисунок 2 – Решение задачи
Рисунок 2 – Решение задачи

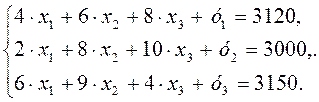

 .
.




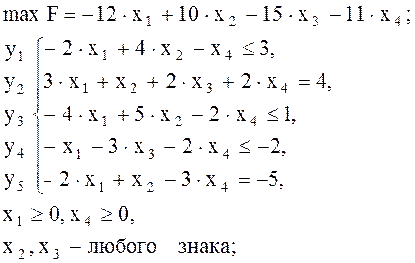




 .
.

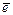 ) – неориентированный граф, то ему соответствует симметричная матрица смежности, так как дуги (Еi, Еj) и (Еj,Еi) существуют одновременно. Если G=(E,
) – неориентированный граф, то ему соответствует симметричная матрица смежности, так как дуги (Еi, Еj) и (Еj,Еi) существуют одновременно. Если G=(E, 
 является начальной вершиной дуги
является начальной вершиной дуги 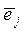 (если ребра имеют общую вершину), и нулю во всех остальных случаях. В таблице 14 приведены матрица смежности ребер и (дуг) графа, изображенного на рисунке 3.
(если ребра имеют общую вершину), и нулю во всех остальных случаях. В таблице 14 приведены матрица смежности ребер и (дуг) графа, изображенного на рисунке 3.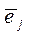


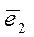














 ставится значение ε (E,
ставится значение ε (E, 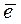 , ε (E,
, ε (E,