
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения с разделенными и разделяющимися переменными
Рассмотрим дифференциальное уравнение вида
которое называется уравнением с разделяющимися переменными (здесь и в дальнейшем все функции подразумеваются непрерывными в некоторой области). Предполагая, что
Интегрируя левую и правую части, получим общий интеграл уравнения (5.1):
Дифференциальное уравнение типа (5.2) или вида
называют уравнением с разделенными переменными. Его общий интеграл есть
Уравнение вида
в которых коэффициенты при дифференциалах распадаются на множители, зависящие только от x и только от
Лекция 10. §5. Однородные уравнения первого порядка Определение 1. Функция
Определение 2. Уравнение первого порядка
называется однородным уравнением, если функция Метод решения однородного уравнения следующий. Определим новую функцию и(х) с помощью соотношения
Тогда будем иметь
Подставляя это выражение производной в исходное уравнение, получим уравнение с разделяющимися переменными
Интегрируя, найдем
Подставляя вместо u отношение Замечание. Уравнение вида К однородным уравнениям приводятся уравнения вида
Если
где p и q константы, пока неизвестные. Подберем
При этом условии уравнение (6.2) становится однородным:
Решив это уравнение и, перейдя снова к x и §5.1. Уравнения в полных дифференциалах
Рассмотрим дифференциальное уравнение
Предположим, что функции
Определение. Если левая часть уравнения (9.1) представляет собой полный дифференциал некоторой функции Другими словами, уравнение (9.1) представляется в виде Теорема. Для того чтобы уравнение (9.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы во всех точках области
Общий интеграл уравнения (9.1) имеет вид Лекция 11 §6. Линейные уравнения первого порядка Определение.Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной вида
где Будем искать решение уравнение (7.1) в виде произведения двух функций
Дифференцируя обе части этого равенства, находим
Подставляя полученное значение производной
Выберем функцию
Разделяя переменные в этом дифференциальном уравнении, находим
Подставляя найденное значение
Окончательно, Уравнения Бернулли Уравнение вида
где
тогда
Отсюда получим линейное дифференциальное уравнение
Найдя его общий интеграл и, подставив вместо Замечание. Уравнение Бернулли можно решить таким же методом, как и линейное уравнение с помощью замены
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.25.74 (0.01 с.) |
 , (5.1)
, (5.1) , преобразуем его следующим образом:
, преобразуем его следующим образом: . (5.2)
. (5.2)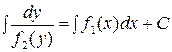 .
.
 .
. , (5.3)
, (5.3)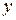 , также называется уравнением с разделяющимися переменными. Общий интеграл этого уравнения имеет вид
, также называется уравнением с разделяющимися переменными. Общий интеграл этого уравнения имеет вид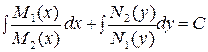 .
. называется однородной функцией
называется однородной функцией  -го измерения относительно переменных x и
-го измерения относительно переменных x и 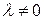 и любых х и у из области определения функции справедливо тождество
и любых х и у из области определения функции справедливо тождество .
. (6.1)
(6.1) , т.е.
, т.е.  .
. .
. .
.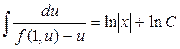 .
. , получим общий интеграл уравнения (6.1).
, получим общий интеграл уравнения (6.1). будет однородным в том и только в том случае, когда
будет однородным в том и только в том случае, когда  и
и  являются однородными функциями одного и того же измерения.
являются однородными функциями одного и того же измерения.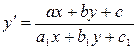 . (6.2)
. (6.2) , то уравнение (6.2) есть однородное. Пусть теперь
, то уравнение (6.2) есть однородное. Пусть теперь 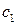 и c отличны от нуля. Сделаем замену переменных
и c отличны от нуля. Сделаем замену переменных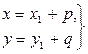 , (6.3).
, (6.3). и
и  так, чтобы выполнялись равенства
так, чтобы выполнялись равенства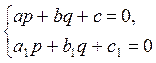 . (6.4)
. (6.4)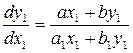 .
. уравнение (6.2) приводится к уравнению с разделяющимися переменными.
уравнение (6.2) приводится к уравнению с разделяющимися переменными. дифференцируемы в некоторой области
дифференцируемы в некоторой области  .
.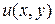 , то (9.1) называется уравнением в полных дифференциалах.
, то (9.1) называется уравнением в полных дифференциалах. ; откуда, интегрируя, найдем его общий интеграл
; откуда, интегрируя, найдем его общий интеграл  .
.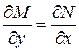 .
. (или
(или  ). Здесь (
). Здесь ( ,
,  ) - некоторая точка из D.
) - некоторая точка из D. , (7.1)
, (7.1) и
и  - непрерывные функции от x.
- непрерывные функции от x.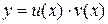 .
. .
.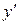 в уравнение (7.1.), имеем
в уравнение (7.1.), имеем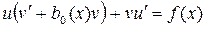 . (7.2).
. (7.2). так, чтобы
так, чтобы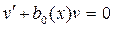 .
. .
.
 .
. .
. ,
, называется уравнением Бернулли. Уравнение Бернулли приводится к линейному дифференциальному уравнению. Для этого сделаем замену
называется уравнением Бернулли. Уравнение Бернулли приводится к линейному дифференциальному уравнению. Для этого сделаем замену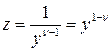 ,
, .
. .
.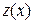 выражение
выражение  , получим общий интеграл уравнения Бернулли.
, получим общий интеграл уравнения Бернулли.


