
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства векторного произведения. ⇐ ПредыдущаяСтр 3 из 3
1. Доказательство: Из определения следует, что векторы
2. Докажем это свойство для 3. Без доказательства. .6. Геометрический смысл векторного произведения: Модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах. 10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов. Определение 4.3. Векторы, параллельные одной плоскости, называются компланарными. Очевидно, что два вектора всегда компланарны. Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю. Определение 4.2. Смешанным произведением трех векторов Свойства смешанного произведения. 1. Доказательство этих соотношений проводится аналогично выводу формулы (4). Чтобы их запомнить заметим, что при «циклической перестановке» векторов (вектор передвигается на следующее место, а последний – на первое) знак не меняется, а при перестановке двух соседних векторов знак смешанного произведения меняется. 2. Геометрический смысл смешанного произведения.Модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах, как на ребрах. Параметрическое и каноническое уравнения прямой на плоскости. Так как координаты вектора Выражая параметр
Опуская
где Приведенное и общее уравнения прямой. Угол между прямыми. Расстояние от точки до прямой. Критерий перпендикулярности.
общее уравнение прямой
приведенное уравнение прямой Таким образом, угол между прямыми находится по формуле:
В частности, если угол составляет
Критерием параллельности двух невертикальных прямых на плоскости
т.к.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.9 (0.006 с.) |
 (антикоммутативность).
(антикоммутативность). и
и  имеют одинаковую длину и противоположные направления:
имеют одинаковую длину и противоположные направления: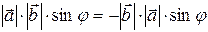 .
. (ассоциативность).
(ассоциативность).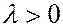 : вектор
: вектор 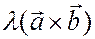 имеет то же направление, что и вектор
имеет то же направление, что и вектор 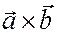 . Вектор
. Вектор  при
при  ,
,  . Аналогично проводится доказательство для случая
. Аналогично проводится доказательство для случая  .
. (дистрибутивность).
(дистрибутивность). ,
,  и
и  называется число, равное
называется число, равное  , т.е. скалярному произведению векторного произведения первых двух на третий вектор.
, т.е. скалярному произведению векторного произведения первых двух на третий вектор. .
. и известны координаты вектора
и известны координаты вектора  , то можно записать векторное уравнение прямой (1) в координатах:
, то можно записать векторное уравнение прямой (1) в координатах:  Полученную систему называют параметрическим уравнением прямой.
Полученную систему называют параметрическим уравнением прямой. из каждого уравнения параметрической системы (2), получим
из каждого уравнения параметрической системы (2), получим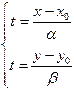 Û
Û 
 , (3)
, (3)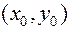 - координаты точки, через которую проходит прямая, а
- координаты точки, через которую проходит прямая, а  - координаты направляющего вектора.
- координаты направляющего вектора. .
.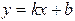 , где
, где  ,
,  .
. . (9)
. (9) , то
, то  . Это возможно, если
. Это возможно, если 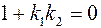 . Получаем критерий перпендикулярности прямых
. Получаем критерий перпендикулярности прямых или
или  (10)
(10) и
и  является равенство:
является равенство: , (11)
, (11) .
.


