Периодические режимы в нелинейных системах. автоколебательный режим

В автоколебательном режиме работы формирование импульсов и переключение усилительных каскадов происходят независимо от внешнего воздействия на схему мультивибратора. В автоколебательном режиме работы мультивибратор исходного положения не имеет и после каждого переключения находится в одном из временно устойчивых состояний. В автоколебательном режиме импульсного устройства развитие лавинообразного процесса опрокидывания связано с внутренним источником перепадов тока в виде хронирующей индуктивности. Ждущий или автоколебательный режим развертки устанавливают ручкой Режим запуска, имеющей три основных положения. Первое положение используют для наблюдения периодических процессов в автоколебательном режиме развертки, второе-для наблюдения апериодических процессов в ждущем режиме развертки, в третьем положении колебания генератора развертки срываются. [7]Именно такой автоколебательный режим работы двигателя наблюдается при нередко встречающемся на практике дефекте - западании толкателя микропереключателя, когда его контакты остаются постоянно разомкнутыми. Эта неисправность может быть легко устранена заменой или промыванием в чистом бензине микропереключателя, снятого с карбюратора. [8]Проведите исследование автоколебательных режимов для ММ 5.1 - 1, 5.1 - 5, 5.1 - 6, воспользовавшись методом определения периодических режимов работы нелинейных автоколебательных систем, в котором частное периодическое решение ищется в виде нелинейной комбинации заданных функций времени. [9]При возмущениях автоколебательного режима это определяет и низкочастотность спектра Z (f) относительно полосы пропускания разомкнутого контура. [10]Установившиеся параметры автоколебательного режима определяются давлением, конструктивными элементами гидросервомотора и положением втулок регулятора амплитуды. [11]Для нахождения автоколебательных режимов и исследования их устойчивости применим метод эквивалентной линеаризации. [12]

 

Билет 6

Дифференциальные уравнения элементов и систем Преобразование Лапласа

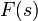Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими. Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных. Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него. Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y '(x), y ''(x),..., y ⁽ⁿ⁾(x) до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.где x[nT] - решетчатая функция, которая представляет собой значение непрерывной функции в дискретные моменты времени.При x(t) = 1(t) . Для любого x(t) . (3)Это физически не реализуемо и является математической идеализацией, вводимой для упрощения исследования дискретных систем.Реальный импульсный элемент (рис. 4) - импульсный элемент с конечной длительностью импульса. Он состоит из идеального импульсного элемента и формирователя.Формирователь преобразует идеальные импульсы в импульсы длительности - gT