
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические функции двойного, половинного аргумента.
1. Тригонометрические функции двойного аргумента:
2. Формулы понижения степени:
3. Тригонометрические функции половинного аргумента:
27. Преобразование суммы и разности одноименных тригонометрических функций в произведение. 1. Сумма синусов
2. Разность синусов
3. Сумма косинусов
4. Разность косинусов
5. Сумма тангенсов
6. Разность тангенсов
7. Сумма котангенсов
8. Разность котангенсов
1) Объясним первую формулу: x + y x – y Она поучена из формул синуса сложения и разности аргументов: sin (α + β) = sin α cos β + sin β cos α sin (α – β) = sin α cos β – sin β cos α. Сложим две формулы: sin (α + β) + sin (α – β) = sin α cos β + Таким образом, sin (α + β) + sin (α – β) = 2 sin α cos β. К этой формуле вернемся в конце наших вычислений. Теперь введем новые переменные: вместо α + β напишем х, вместо α – β напишем у. Тогда: sin х + sin у = 2 sin α cos β. В то же время, введя новую переменную, мы получили систему уравнений. Решим ее методом алгебраического сложения: │α + β = х
│α + β + α – β = х + у
│2α = х + у
Вернемся к полученной нами сумме двух формул сложения аргументов: sin х + sin у = 2 sin α cos β. Осталось подставить в них полученные значения α и β, чтобы в итоге получить нашу формулу: x + y x – y 2) Вторая формула из таблицы логически вытекает из первой и доказывается просто. Вспомним свойство нечетности синуса: sin (–y) = – sin y. Из этого следует, что sin x – sin y = sin x + (–sin y). Следовательно: x + (–y) x – (–y) х – у х+ у Таким образом: x – y x + y
Аналогично преобразуются в произведение суммы косинусов. Преобразуем еще суммы тангенсов и котангенсов. Порядок прост: представляем тангенсы и котангенсы как отношение синусов и косинусов, находим для полученных дробей общий знаменатель и применяем формулы сложения. То есть совершаем всего три действия: sin x sin y sin x cos y + cos x sin y sin ( x + y )
cos x cos y cos x sin y + sin x cos y sin ( x + y ) ctg x + ctg y = ——— + ——— = ———————————— = —————— Преобразование разностей в произведение осуществляется таким же образом. 28. Преобразование произведения одноименных тригонометрических функций в сумму и разность
Первая формула получается сложением формул синуса суммы и синуса разности, в каждой из которых левую и правую часть поменяем местами:
Вторая формула получается сложением, а третья — вычитанием следующих равенств (формул сложения для косинуса):
Окончательно:
Применение этих формул иногда упрощает преобразование тригонометрического выражения. 29. Простейшие тригонометрические уравнения y=sin x, y=cos x, y=tg x, y=ctg x. Уравнение sin x = a Условия: 1) | a | ≤ 1 2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения sin x = a:
Частные случаи, когда уравнение sin x = а имеет более простое решение:
Уравнение cos x = a Условия: 1) | a | ≤ 1 2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Уравнения tg x = a и ctg x = a. Формула решения уравнения tg x = a:
Формула решения уравнения ctg x = a:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.012 с.) |
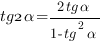






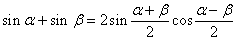

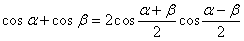



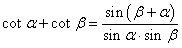

 ,
, ,
, .
.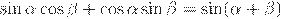 ,
,  ,
,  ,
, ,
,  ,
, ,
, 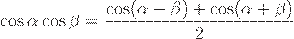 .
.


