
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двойное векторное произведение. ⇐ ПредыдущаяСтр 7 из 7
Определение 1. Двойное векторное произведение векторов Выразим двойное векторное произведение через скалярное. Пусть Пусть вектор Тогда
Для того, чтобы найти Имеем
Отсюда видно, что
Пример 1. Доказать тождество Якоби:
Имеем
Суммируя эти равенства, получим тождество Якоби. Пример 2. Вычислить Имеем: (
§15.Уравнение прямой линии на плоскости. 10. Векторное, параметрическое, общее и каноническое уравнение прямой.
Зафиксируем на плоскости аффинную систему координат, определяемую точкой О - началом координат, базисным вектором Тогда " точка плоскости Зафиксируем на плоскости некоторую прямую линию. Определение 1. Всякий ненулевойвектор Пусть есть точка Другими словами это означает, что С другой стороны всякая точка М, для которой выполнено уравнение (1) принадлежит прямой в силу определения произведения вектора на число. Таким образом т. М Если обозначить радиус вектора т. также называется векторным уравнением прямой. Если
- параметрическое уравнение прямой на плоскости, проходящей через т.
Рис.1 Исключая из уравнения (3) параметр t получаем - каноническое уравнение прямой на плоскости. Уравнение (4) необходимо воспринимать, как пропорцию, если Приведем уравнение (4) к общему знаменателю:
- общее уравнение прямой на плоскости. Так как Показали, что " прямая является алгебраической линией первого порядка. Покажем, что " алгебраическая линия первого порядка на плоскости является прямой. Действительно, уравнение (5) имеет частное решение, например:
В качестве Покажем, что т. Действительно, по построению
0=0 получаем тождество Таким образом доказана следующая теорема: Теорема 1. Прямые на плоскости – алгебраические линии первого порядка. Из доказательства теоремы 1 следует, что если

Рис.2. Если
Вместе с каноническим уравнением (4) используется уравнение прямой, проходящей через 2 точки: если l проходит через точку и называется уравнением прямой, проходящей через т. ??? частные случаи уравнения (5): 1. А=0 прямая ∥-ая Ox 2. B=0 прямая ∥-ая Oy 3. C=0 проходящая через начало координат 4. A=C=0 ось Ox 5. B=C=0 ось Oy
20. Взаимное расположение прямых на плоскости. Полуплоскости. Пусть на плоскости задана аффинновая система координат Утверждение 1. Для того, чтобы прямые
соответственно совпадали необходимо и достаточно, чтобы |Þ Возьмем т. Умножая первое уравнение на Формулы (10), (11) эквивалентны (9) Ü| пусть выполняется (9), тогда уравнения (7) и (8) эквивалентны Þ соответствующие прямые совпадают, ч.т.д.∎ Утверждение 2. Прямые
Доказательство. |Þ прямые параллельны и не совпадают Þ возможно лишь при условии Ü| Если выполняется первое равенство Þ прямые параллельны, а не выполнение второго Þ система (7), (8) несовместна Þ прямые параллельны и не совпадают, ч.т.д.∎ Следствие (из 1,2). Прямые Утверждение 3. Пусть прямые
Т.е. уравнение (14) – линейная комбинация (7,8) Доказательство. |Þ Очевидно, а именно, если уравнение l3 задается (14), то она проходит через т. Ü| пусть l3 проходит через т. Возьмем на прямой l3 " т. Покажем, что уравнение для l3 пропорционально (14) с выбранными Т.к. т. По построению эта прямая проходит через т. Уравнение (14) называется уравнением пучка прямых, проходящих через т.
30. Прямая линия на плоскости с прямоугольной системой координат. Нормальное уравнение прямой. Пусть на плоскости задана прямоугольная декартова система координат Отметим, что угол между прямыми принимает значение от Поэтому угол между прямыми определяется углом между векторами. Получаем, что прямые (7), (8) в прямоугольной системе координат ортогональны Û Отметим, что только прямоугольной декартовой системе координат вектор В дальнейшем построим нормальное уравнение на плоскости. В начале введем уравнение прямой в полярной системе координат. Пусть полярная ось совпадает с Ox и l1 – ось, проходящая через начало координат перпендикулярно прямой l.
Рис.3.
Пусть прямая
Последнее условие является необходимым и достаточным, для того, чтобы т. М
где
Другими словами,
где Получаем:
Отметим, что Пусть прямая l:
Если С= 0, то знак Нормальное уравнение прямой удобно для нахождения расстояния между от произвольной точки плоскости до прямой.
 
Рис.4.
Произвольная точка
 Таким образом, получили, что расстояние от точки до прямой вычисляется следующим образом: в левую часть нормального уравнения этой прямой необходимо подставить координаты т. и полученную величину взять по модулю. Замечание. Из рисунка видно, что если т. Последнее может быть использовано, чтобы узнать лежит ли т. Пример. § 16. Уравнение плоскости в пространстве. 10. Различные виды уравнения на плоскости.
Принципы построения уравнения плоскости в пространстве во многом совпадают с построением прямой на плоскости. Это связано с тем, что размерность прямой отличается от??? плоскости на единицу. Размерность плоскости отличается на единицу от??? пространства. Поэтому плоскость определяется двумя линейно-независимыми векторами и точкой, через которую эта плоскость проходит. Утверждение 1. Пусть в плоскости Доказательство. |Þ Пусть т. М лежит в плоскости, тогда это означает, что Ü| если справедливо (1), то Уравнение (1) будет называться уравнением плоскости в векторной форме. Оно означает лишь, что плоскость проходит через т. Тогда (1) перепишем: Если теперь зафиксировать координаты векторов Уравнение (3) называется параметрическим уравнением плоскости. Если его переписать в виде:
Представляет собой линейную зависимость столбцов матрицы: Разлагая этот определитель по первому столбцу получим:
где Уравнение (4) является уравнением плоскости, проходящей через т.
Если в плоскости заданы 3 точки Уравнение плоскости, проходящей через 3 точки: Если в уравнение (5) раскрыть скобки и обозначить Отметим, что в силу неколлинеарности Таким образом, показали, что любое уравнение плоскости может быть записано в виде уравнение первой степени. Докажем и обратное: любое уравнение первой степени вида (8) представляет собой уравнение некоторой плоскости. Пусть в (8) Покажем, что плоскости, проходящие через полученную точку параллельно
доказана теорема 1: Пусть в пространстве- в точности поверность первого порядка.
20. Взаимное расположение плоскостей в пространстве. Полупространства. Утверждение 1. Вектор Доказательство. Для доказательства утверждения необходимо и достаточно показать, что, если Пусть Утверждение 2. Плоскости
параллельны Доказательство. Ü| Плоскости параллельны, если вектор параллельный одной плоскости, будет параллелен другой. Поэтому, если выполняется условие (12), то в силу утверждения 1 плоскости параллельны. |Þ пусть
Утверждение 3. Плоскости Доказательство. Ü| очевидно |Þ пусть плоскости совпадают, тогда первые два равенства следуют из утверждения 2 и доказываем третье равенство. Пусть т В силу соотношения (12) получим: Умножим первое уравнение последней системы на Утверждение 4. Плоскости Утверждение 5. Плоскости Утверждение 6. Пусть плоскости
где Доказательство. Аналогично для пучка прямых, так как (15) – это уравнение пучка плоскостей, проходящих через l.
30. Плоскость в пространстве с прямоугольной декартовой системой координат. Пусть в пространстве задана прямоугольная декартова система координат Условие перпендикулярности двух векторов в ортогональном базисе:
В ортогональном базисе коэффициенты А, В, С общего уравнения (8) можно??? как коэффициенты векторной нормали.
Вектор нормали используется для решения задач нахождения угла между плоскостями, угла между прямой и плоскостью и т.д. По аналогии с прямой на плоскости строится нормальное уравнение плоскости.
Пусть в пространстве с прямоугольной декартовой системой координат задана плоскость Пусть т. N – это точка пересечения прямой l с плоскостью Тогда произвольная т. М пространства Другими словами,
 - единичный вектор, являющийся масштабным вектором оси l. - единичный вектор, являющийся масштабным вектором оси l.
 , где , где  - углы с осями - углы с осями  . .
Получаем нормальное уравнение плоскости: § 17. Уравнение прямой в пространстве.
10. Уравнение прямой в произвольной аффиновой системе координат. В предыдущем § было указано, что если две плоскости пересекаются, то они пересекаются по прямой. Поэтому в произвольной аффиновой системе координат уравнение прямой в следующем виде:
Плоскости Тогда система (1) при условии (2) представляет систему линейно независимых уравнений, совместную и имеет общее решение следующего вида: где
Геометрически (3) означает, что т.
Можно переписать в виде: где Перепишем уравнение (3): - параметрическое уравнение прямой в пространстве. Если исключить из (4) параметр t получим: - каноническое уравнение прямой в пространстве, (5) – пропорция. Пример. Если Если необходимо написать уравнение прямой, проходящей через две точки
- уравнение прямой, проходящей через две точки. Каждая прямая может быть представлена как линия пересечения двух плоскостей.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.231.155 (0.205 с.) |
 ,
,  ,
,  это произведение вида
это произведение вида  .
. Þ
Þ 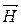 ^
^  . Тогда, в силу
. Тогда, в силу  . Умножим это равенство скалярно на
. Умножим это равенство скалярно на  .
. в обоих случаях). Тогда
в обоих случаях). Тогда  Þ
Þ 
 , такое что
, такое что  ,
,  .
. .
. , вычислим левую и правую части в некотором базисе. Пусть вектор
, вычислим левую и правую части в некотором базисе. Пусть вектор  направлен вдоль вектора
направлен вдоль вектора  лежит в плоскости векторов
лежит в плоскости векторов  определяется из условия, что
определяется из условия, что  ,
,  ,
,  .
. ,
,  .
. .
. .
. . Итак, справедлива формула:
. Итак, справедлива формула: .
. .
. ,
,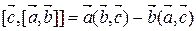 .
. .
. )
) 
 .
.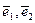
 определяется координатами
определяется координатами  .
.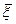 ∥ прямой l называется направляющим вектором этой прямой.
∥ прямой l называется направляющим вектором этой прямой. , тогда производная точки
, тогда производная точки 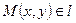 лишь при условии, когда вектор
лишь при условии, когда вектор  коллинеарен
коллинеарен  (1)
(1) выполняется (1). Уравнение (1) называется векторным уравнением прямой.
выполняется (1). Уравнение (1) называется векторным уравнением прямой. через
через  и
и  соответственно, то
соответственно, то  и уравнение (1):
и уравнение (1):  , (2)
, (2) , то (2) в координатах:
, то (2) в координатах: (3)
(3) в направлении
в направлении  .
.

 (4)
(4) , то это прямая ∥-ая оси Oy, проходящей через т.
, то это прямая ∥-ая оси Oy, проходящей через т.  .
. . Если обозначить
. Если обозначить  получаем:
получаем:  (5)
(5) , то один из коэффициентов А или В отличен от нуля ⇒ уравнение (5) представляет собой уравнение первого порядка.
, то один из коэффициентов А или В отличен от нуля ⇒ уравнение (5) представляет собой уравнение первого порядка. , то можно выбрать
, то можно выбрать  ,
,  , тогда полученное решение можно???, как координаты точки
, тогда полученное решение можно???, как координаты точки  , через которую проходит искомая прямая.
, через которую проходит искомая прямая. прямой K вектор
прямой K вектор 
 прямой лишь при условии, когда её координаты удовлетворяют уравнению (5).
прямой лишь при условии, когда её координаты удовлетворяют уравнению (5). , т.е.
, т.е. 
 является направляющим вектором этой прямой.
является направляющим вектором этой прямой.


 , то из уравнения (5) получаем:
, то из уравнения (5) получаем:  , т.е.
, т.е.  , где
, где  .
.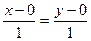 .
. , то
, то  можно выбрать K в качестве направляющего вектора прямой, поэтому уравнение
можно выбрать K в качестве направляющего вектора прямой, поэтому уравнение  (6)
(6) .
.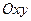 .
. и
и  , заданные уравнениями
, заданные уравнениями  (7)
(7) (8)
(8) (9)
(9) l1 и l2 совпадают, это означает, что их направляющие вектора
l1 и l2 совпадают, это означает, что их направляющие вектора  и
и  коллинеарные, т.е.
коллинеарные, т.е.  (10)
(10)
 этим прямым, тогда
этим прямым, тогда  ,
, и прибавляя по??? в силу (10):
и прибавляя по??? в силу (10):  (11)
(11) (12)
(12) ,
, это возможно при выполнении (12)
это возможно при выполнении (12) (13)
(13) (14)
(14)

 .
.
 .
. и
и  отлично от нуля. Поэтому уравнение
отлично от нуля. Поэтому уравнение  является уравнением первой степени Þ определяет некоторую прямую.
является уравнением первой степени Þ определяет некоторую прямую. , т.к. через две точки плоскости, то она совпадает с прямой
, т.к. через две точки плоскости, то она совпадает с прямой  .
. , угол между направляющими
, угол между направляющими  .
. (15)
(15) является перпендикулярной к прямой
является перпендикулярной к прямой 




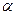



 и пусть длина
и пусть длина ,
, 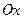 . Если т. М лежит на l1, то очевидно, что проекция
. Если т. М лежит на l1, то очевидно, что проекция 
 .
. или
или  , (16)
, (16) - расстояние от т. М до начала координат,
- расстояние от т. М до начала координат, и
и 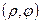 - полярные координаты т. М. Таким образом, уравнение (16) является уравнением прямой в полярной системе координат. Уравнение (16) можно переписать:
- полярные координаты т. М. Таким образом, уравнение (16) является уравнением прямой в полярной системе координат. Уравнение (16) можно переписать: 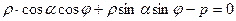

 ,
,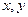 - координаты т. М в соответствующей прямоугольной декартовой системе координат.
- координаты т. М в соответствующей прямоугольной декартовой системе координат. (17) – нормальное уравнение прямой на плоскости, где
(17) – нормальное уравнение прямой на плоскости, где и
и  - координаты ортонормали. Покажем, что общее уравнение прямой привели к нормальному виду.
- координаты ортонормали. Покажем, что общее уравнение прямой привели к нормальному виду. , тогда нормальное уравнение получается умножением на некоторый нормирующий множитель
, тогда нормальное уравнение получается умножением на некоторый нормирующий множитель  :
:  при этом
при этом  , знак
, знак 



 ,
,  . Очевидно, что расстояние от
. Очевидно, что расстояние от 

 . В первом случае:
. В первом случае:  , во втором -
, во втором -  .
. .
. задана т.
задана т. 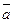 и
и  . Тогда т.
. Тогда т.  . (1)
. (1) компланарны Þ в силу неколлинеарности
компланарны Þ в силу неколлинеарности 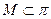 , ч.т.д.∎
, ч.т.д.∎ - векторное уравнение плоскости. (2)
- векторное уравнение плоскости. (2) , то уравнение (2):
, то уравнение (2):  (3)
(3)
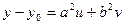
 ,
, = 0 (4)
= 0 (4) (5)
(5) (6)
(6)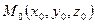 и параллельно
и параллельно  .
. , то в качестве векторов
, то в качестве векторов 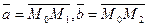 .
. (7)
(7) , то
, то 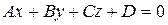 - общее уравнение плоскости (8)
- общее уравнение плоскости (8) хотя бы один из определителей (6) отличен от нуля Þ уравнением первой степени.
хотя бы один из определителей (6) отличен от нуля Þ уравнением первой степени.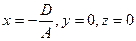 , которое определяет координаты точки, через которую проходит плоскость. А вектора имеют значения
, которое определяет координаты точки, через которую проходит плоскость. А вектора имеют значения  .
. , где
, где  эквивалентно (8)
эквивалентно (8) параллелен плоскости
параллелен плоскости 
 (9)
(9) ,
,  ,
,  , проверим, что
, проверим, что  . Подставляя в уравнение (8):
. Подставляя в уравнение (8): 
 ,ч.т.д.∎
,ч.т.д.∎ (10)
(10) (11)
(11) (12)
(12) , тогда вектора
, тогда вектора  , которые параллельны плоскости
, которые параллельны плоскости  , должны быть параллельны
, должны быть параллельны  Þ в силу утверждения 1 выполняется:
Þ в силу утверждения 1 выполняется: , ч.т.д.∎
, ч.т.д.∎ (13)
(13)
 .
. мы доказали уравнение (13), ч.т.д.∎
мы доказали уравнение (13), ч.т.д.∎ (14)
(14) - неколлинеарны.
- неколлинеарны. проходит через эту прямую Û её уравнение имеет вид:
проходит через эту прямую Û её уравнение имеет вид: , (15)
, (15) одновременно.
одновременно. . Пусть плоскость
. Пусть плоскость  - некоторый вектор
- некоторый вектор  , тогда
, тогда  .
.
 .
.

 , (16)
, (16) .
. 
 (1)
(1) (2)
(2)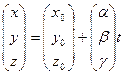 , (3)
, (3) - частные решения (1),
- частные решения (1), 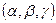 - ФСР соответствующей системы линейно ОУ.
- ФСР соответствующей системы линейно ОУ. получается прибавлением к радиус-вектору т.
получается прибавлением к радиус-вектору т. 
 Таким образом,
Таким образом, 
 , (3’)
, (3’) - радиус-вектор т.
- радиус-вектор т.  (4)
(4) (5)
(5)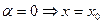 , значит прямая лежит в плоскости
, значит прямая лежит в плоскости  равны нулю, то прямая лежит в плоскостях
равны нулю, то прямая лежит в плоскостях  , что означает есть линия пересечения плоскостей – прямая параллельная оси
, что означает есть линия пересечения плоскостей – прямая параллельная оси  .
. .
. - направляющий вектор
- направляющий вектор (6)
(6)


