
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный полином Лагранжа-СильвестраСтр 1 из 7Следующая ⇒
Функции от матриц. Простейшими функциями от матриц являются полиномы. Если задан числовой полином относительно
Рассмотрим теперь произвольную функцию
Опр. Если для функции Если функция f не определена на спектре матрицы А, то не определенно и f(A). Лемма. Значения полиномов g(λ) и h(λ) на матрице А совпадают тогда и только тогда, когда они имеют одинаковые значения на спектре матрицы А. Опр. Пусть функция f определена на спектре матрицы А. Тогда f(A)=g(A), где
Интерполяционный полином Лагранжа-Сильвестра Опр. Полином r(λ), определяемый интерполяционными условиями Называется интерполяционным полиномом Лангранжа-Сильвестра функция Опр. Если функция f(λ) определена на спектре матрицы А, а r(λ) - соответствующий интерполяционный полином Лагранжа-Сильвестра, то f(А) = r(А). Виды интерполяционный полином Лангранжа-Сильвестра: 1. где все собственные значения различны: 2. есть кратные собственные, но минимальный имеет простые корни: 3. минимальный имеет кратные корни:
Свойство функции матрицы: 1. Если 2. Если две матрицы А и В подобны и матрица S преобразует А в В: 3. Если А- блочно-диогональная матрица: A=diag{A1,A2,…,Au}, то f(A)=diag{f(A1),f(A2),…,f(Au)}.
Теорема о существовании псевдообратной матрицы Мура-Пенроуза. Опр. Матрица Теорема. Для любой матрицы А псевдообратная матрица Мура-Пенроуза существует, единственна и выражается по формуле
Док-во: Докажем существование матрицы
Умножим последнее равенство слева на В*:
Теперь умножая последнее равенство справа на В*, получим Рассмотрим матрицу Тогда используя А=ВС и
Сопряжённое отображение Пусть дано линейное отображение А: Опр. Отображение Теорема. Для любого заданного линейного отображения А сопряженное отображение Докво. Построим отображение Из этого следует, что для данного функционала Т.о. сопряженное отображение определяется как композиция Докажем единственность Пусть
Теорема. Пусть А:
Унитарное подобие. Так как для унитарной матрицы U*=U-1, то преобразование А → U*AU, определенное на Сn×n, явл. подобием которое называется унитарным подобием. Опр. Матрица B Є Сn × n называется унитарно подобной матрице А Є Сn × n, если найдется унитарная матрица U Є Сn × n , такая, что B = U*AU. Если Г можно выбрать вещественной (а значит, ортогональной), то В называется ортогонально подобной матрице А. Рассмотрим два специальных типа унитарных матриц, которые осуществляют преобразования унитарного подобия, весьма важные для вычисления собственных значений. Пример 1. (Плоские вращения). Матрица U(θ;i,j) осуществляет вращение (на угол θ) в плоскости координат i,j. Заметим, что если матрица умножается слева на U(θ; i, j), то в ней изменяются только i-я и j-я строки, а если она умножается справа, то изменяются только i-й и j-й столбцы. Таким образом, при переходе к унитарно подобной матрице, осуществляемом с помощью U(θ;i,j), происходит изменение только строк и столбцов с номерами i и j. Унитарное подобие, существляемое посредством плоских вращений, используется при вычислении собственных значений. Пример 2. (Преобразования Хаусхолдера). Возьмем произвольный ненулевой вектор w ∈ Cn и образуем матрицу Uw = E – tww* (Uw ∈ Cn × n), где t = 2(w*w)-1. Заметим, что w*w - это положительный скаляр, ww* ∈ Cn × n матрица. Если вектор w был нормирован (w*w = 1), то t должно быть равно 2, а матрица Uw должна иметь вид Uw = E − 2ww*. Часто образуют матрицу Uw, выбирая заранее именно нормированный вектор w. Любая матрица Uw называется преобразованием Хаусхолдера.
Теорема. Дляунитарно подобных матриц A и B из Сn×n имеет место равенство Доказательство:
Достаточность. Рассмотрим утверждение а) для вектора (x + y) ∈
Поскольку Возьмем в (6.1) x =
Возьмем x = i − i Из (6.2) и (6.3) следует, что b) По спектральной теореме для нормальных матриц нормальная матрица унитарно диагонализуема, т.е. A = Рассмотрим следовательно А - эрмитова. c) Положим S =
Теорема Рэлея-Ритца Теорема Рэлея-Ритца. Пусть A -эрмитова и ее собственные значения упорядочены (Пусть A – эрмитова,
Доказательство. Поскольку матр. А – эрмитова, то по спектральной теореме для эрмитовых матриц сущ. такие унитарные март. Каждый сомножитель
Поскольку март. U унитарна, а унитарные матр.изометричны, то имеют место равенства
Таким образом, справедливы соотношения:
что и доказывает (2). Покажем, что оценки в соотношении (2) точны. Действительно, если x – собст.векторматр. A, соответствующий собственному значению λ1, то
Точность оценки сверху устанавливается аналогично. Остальные утверждения является простыми следствиями соотношений(2). Покажем, например, справедливость (3). При Это неравенство обращается в равенство, когда x- собственный вектор матрицы A, соответствующий собственному значению Наконец, при
Таким образом, равенство (5) эквивалентно следующему
Рассуждения для минимального собственного значения
Полярное разложение матриц Теорема (Полярное разложение). Если A∈ Более того, Доказательство. Положим Где U,V – матрицы из сингулярного разложения (1). Несложно проверить, что W – унитарная матрица, а H – положительно полуопределенная эрмитова матрица. Тогда имеем:
Далее, так как Применяя полученный результат к
Матричные нормы Опр. Ф-ция ||•||: 1)||A||≥0(неотрицательность); 1а) A||=0 2)||αA||=|αA|| 3)||A+B||≤||A||+||B|| (неравенство треугольника); 4)||AB||≤||A|B|| Примеры матричных нормна 1*. ||A||1 ≡ 2*. ||A||∞ ≡ 3*. ||A||E ≡ 4*. ||A||E ≡ 5*. ||A||M ≡ 6 *.
Доказательство
Следствие. Матричная норма ||•||M, подчиненная векторной норме ||•||V, согласована с этой нормой. Матричная норма, подчиненная векторной норме ||•||∞ Получим оценку сверху для величины ||Ax||∞ ||Ax||∞ Покажем, что эта оценка достигается. Пусть максимум по i имеет место при i=l. Возьмем x=(sign(al1),…,sing(aln)). Имеем Таким образом,
Число обусловленности. Определение. Величина
называется числом обусловленности матрицы A по отношению к матричной норме ||•||. Свойства числа обусловленности 10. Для любой матричной нормы cond(A)≥1. 20. Для любой матрицы A и любого числа α выполняется равенство cond(A) =cond(αA). 30. Для спектральной и евклидовой норм число обусловленности не меняется при умножении матрицы слева и справа на любую унитарную матрицу.
40. Для 1-, 2-, ∞-норм и евклидовой нормы число обусловленности не меняется при перестановке строк и столбцов. 50. Для спектральной нормы число обусловленности любой матрицы равно отношению максимального сингулярного числа к минимальному.
Сходимость матриц Определение. Матрица А называется сходящейся, если Лемма. Доказательство . ||Ak||≤||A||k→k→0 0 Теорема. Матрица Доказательство. Пусть Ak→0.Рассмотрим собственный вектор x≠0: Ax=λx. Тогда A2x=A(Ax)=A(λx)=λ(Ax)=λ2x…Akx=λkx→0 Обратно Следствие.
Теорема Гершгорина Теорема Гершгорина и ее следствия. Для произвольной матрицы AЄ
Наиболее полезная и легко применяемая теорема, дающая оценка для собственных значений – теоремы Гершгорина. Теорема Гершгорина (строчная). Все собственные значения матрицы A заключены в объединении n кругов
Кроме того, если объединение k из этих кругов есть связная область, не пересекающаяся с остальными n−k кругами, то в ней находится ровно k собственных значений матрицы A. Теорема (Гершгорина (столбцовая)). Все собственные значения матрицы AЄ
Кроме того, если k из этих кругов образуют область, изолированную от остальных n-k кругов, то в ней находится ровно kсобственных значений матрицы А.
32. Уточнение оценок собственных значений с помощью преобразования подобия. Если относительно матрицы имеется некоторая дополнительная информация, в силу которой собственные значения принадлежат (или не принадлежат) конкретным множествам, то в сочетании с теоремой Гершгорина эта информация может привести к более точной локализации собственных значений. Определяющие свойства некоторых типов матриц и свойства их собственных значений приведены в таблице
Следствие. Пусть
Пусть
33. Локализация собственных значений Неравенство Шура. Теорема Бендиксона. Теорема (Неравенство Шура). Если A = (aij) ∈
причем равенство имеет место тогда и только тогда, когда матрица А нормальная. Доказательство. Согласно теореме Шура сущ. унитарная матрица
Поскольку след у подобных матриц равен, то trAA∗ =trTT∗ (2)
Далее с учётом (2) справедливы соотношения
что и доказывает (1). Равенство возможно тогда и только тогда, когда
Теорема (Бендиксона). Если
Доказательство. Пусть x - нормированный собственный вектор матрицы A, соответствующий собственному значению λk: Ax=λkx, x*x=1. (1). Тогда (Ax)*x=x*A*x=(λkx)*x= Т. к. матр. Bэрмитова, то для нее справедлива теор Рэлея-Ритца:
Отсюда с учетом первого соотношения теоремы Рэлея-Ритца имеем
Аналогично, применяя теоремуРэлея-Ритца к эрмитовой матрице C, получим второе соотношение теоремы.
Невырожденность матриц. Определение. Матрица
Теорема (Адамара). Если А – матрица со строгим диагональным преобладанием, то она обратима. Теорема. Если у матрицы Определение. Матрица
где B и D - квадратныематрицы. В противномслучаематрица A называется неразложимой. Определение. Матрица M(A) с элементами (8.25) называется индикаторной матрицей для A. Теорема. Матрица Определение. Ориентированным путём в графе Г из вершины Pi1в вершину Pik наз.последовательность дуг Длина ориентированного пусть – это чисто луг в нём, если оно конечно. Определение Ориентированный граф называется сильно связным, если в нем любые два узла Pi,Pj соединены ориентированным путем конечной длины, начинающимся в Pi изаканчивающимся в Pj. Теорема. Матрица Следствие Матрица, у которой все элементы ненулевые, неразложима. Теорема Ольги Тауски. Если для неразложимой матрицы А выполняются ослабленные условия Адамара и по крайней мере в одном из этих условий имеет строгого неравенства(>), то матрица А – невырожденная. AE. Теорема. Пусть A,B∈. Если |A| ≤B, тоρ(A)≤ρ(|A|)≤ρ(B). Следствие. ПустьA, В∈. Если 0 ≤ A ≤ B, то ρ(A)≤ρ(B). Лемма. Пусть A∈ иA≥0. Если строчные суммы для А постоянны, то ρ(A)=||A||∞. Если для A постоянны. столбцовые суммы, то ρ(A)=||A||1. Теорема. Пусть A∈ и A≥0. Тогда Следствие. Пусть A∈, А≥0 и. Тогда. В частности, если А>0 или если А неразложима и неотрицательна. Теорема. Пусть A∈ и предположим, чтоА≥0. Тогда для любого положительного вектораxЄCnсправедливы неравенства: Следствие. Пусть A∈, x ∈Rn, и предположим, что A≥0 и x>0. Если числа α,β≥0 таковы, чтоαx≤Ax≤βx, то α≤ρ(A)≤β. Если αx<Ax, то α<ρ(A); если Ax<βx, то ρ(A) <β. Следствие 9.4. Пусть A∈ и A≥0. ЕслиA имеет положительный собственный вектор, то отвечающее ему собственное значение есть ρ(A). Другими словами, если Ax=λx, x>0 и A≥0, то λ=ρ(A) Теорема Перрона-Фробениуса Теорема (Перрона— Фробениуса). Пусть A ∈ а) ρ(A) > 0; b) ρ(A) есть собственное значение матрицы A: ρ(A) = с) для некоторого d) ρ(A) есть алгебраически (а значит, и геометрически) простое собственное значение для A.
Теорема Фань-Цзы. Теорема (Фань Цзы). Пусть A∈C n×n и B∈R n×n, B ≥ 0 и B ≥ |A|. Тогда любое собственное значение матрицыA принадлежит области
Доказательство. Будем считать, что B> 0. Если это не так, то можно рассматривать матрицу B ε ≡ [b ij + ε], где ε> 0. ПриэтомB ε > |A| и ρ(B ε) − (b ii + ε) По теореме Перрона длякакого-то положительного векто-раx имеем Bx = ρ(B)x. Рассматривая это равенство покомпонентно для ∀i = ⌐i, n, имеем ρ(B)x i = Положив в (8.4)p i = x i, убеждаемся в (9.1).
Стохастические матрицы. Определение. Неотрицательная матрица A ∈R n×n, для которой все строчные суммы равны +1, называется (строчной) стохастической матрицей. Столбцовая стохастическая матрица — это матрица, транспонированная к строчной стохастической матрице. Стохастическая матрица A ∈R n×n, для которой A T также является стохастической, называется двоякостохастической. Теорема. Неотрицательная матрица A является стохастической тогда и только тогда, когда она имеет собственное значение 1 с правым собственным вектором e = Кроме того, спектральный радиус стохастической матрицы равен 1. Теорема. Пусть A — неотрицательная матрица с максимальным собственным значением λ. Пусть существует положительный правый собственный вектор x, соответствующий λ. Положим X = diag {x1,..., xn}. Тогда A = λXP X−1, где P — стохастическая матрица. Доказательство. Пусть P = λ −1 X −1 AX. Покажем, что P —стохастическая. Так как по определению собственного вектора и собственного значения Ax = λx, то Теорема (Биркгофа). Матрица A∈R n×n является двоякостохастической в том и только том случае, когда для некоторого N< ∞ существуют матрицы перестановокP 1,..., P N ∈R n×n и положительные числа α 1,..., α N ∈R, такие, что α 1 +... + α N = 1 и A = α 1 P 1 +... + α N P N. Теорема. Если A ∈R n×n — неразложимая стохастическая матрица, то матрица A ∞ =
1. Функции от матриц. 2. Интерполяционный полином Лагранжа-Сильвестра 3. Скелетное разложение матрицы: лемма о ранге, лемма о существовании и неединственности скелетного разложения 4. Свойства компонент скелетного разложения A=BC: лемма о невырожденности В*В, СС* 5. Теорема о существовании псевдообратной матрицы Мура-Пенроуза. 6. Теорема о единственности псевдообратной матрицы Мура-Пенроуза 7. Свойства псевдообратной матрицы Мура-Пенроуза 8. Решение однородных систем линейных алгебраических уравнений с использованием псевдообратной матрицы Мура-Пенроуза 9. Нормальное псевдорешение системы линейных алгебраических уравнений. 10. Матричные уравнения AX = XB 11. Матричные уравнения AX = XA 12. Сопряженное пространство и его базис
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.231.155 (0.218 с.) |
 , то f(A), A
, то f(A), A  , находиться непосредственной подстановкой:
, находиться непосредственной подстановкой: .
.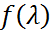 скалярного аргумента
скалярного аргумента  . Пусть
. Пусть (1)― минимальный полином матрицы А степени
(1)― минимальный полином матрицы А степени  . Здесь
. Здесь  ― все различные собственные значения матрицы А:
― все различные собственные значения матрицы А:  .
. (k=1,s) из (1) определены производные
(k=1,s) из (1) определены производные  (2), то говорят, что функция
(2), то говорят, что функция  матрицы А. Совокупность этих значений будем символически обозначать f[δ(A)].
матрицы А. Совокупность этих значений будем символически обозначать f[δ(A)]. - любой полином, принимающий на спектре матрицы А те же значения, что и
- любой полином, принимающий на спектре матрицы А те же значения, что и  ,
,


 , где
, где 
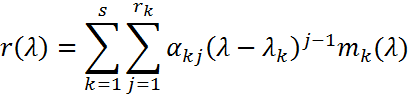
 - собственные значения матрицы n-го порядка А, то
- собственные значения матрицы n-го порядка А, то  - полная система соб. Значений матрицы f(A).
- полная система соб. Значений матрицы f(A). то матрица f(A), f(B) подобны и та же матрица S преобразует f(A) в f(B): f(B)=S-1 f(A)S.
то матрица f(A), f(B) подобны и та же матрица S преобразует f(A) в f(B): f(B)=S-1 f(A)S. называется псевдообратной матрицей Мура-Пенроуза для матрицы
называется псевдообратной матрицей Мура-Пенроуза для матрицы  , если выполнимы следующие условия:
, если выполнимы следующие условия:  ,
,  , где
, где  ,
,  - некоторые матрицы.
- некоторые матрицы. , где В и С- компоненты скелетного разложения А=ВС матрицы А.
, где В и С- компоненты скелетного разложения А=ВС матрицы А.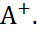 Если А=0, положим
Если А=0, положим  . Пусть А≠0. Рассмотрим разложение А=ВС и будем искать сначала
. Пусть А≠0. Рассмотрим разложение А=ВС и будем искать сначала  Из определения псевдообратной мтарицы имеем:
Из определения псевдообратной мтарицы имеем: .
.
 , аналогично получаем
, аналогично получаем  .
. и покажем, что она удовлетворяет условиям
и покажем, что она удовлетворяет условиям  .
.
 ,
, , где
, где  .
. →
→ 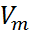 .
. называется сопряженным отображением для А, если для любого
называется сопряженным отображением для А, если для любого  и для любого
и для любого  выполняется следующее соотношение:
выполняется следующее соотношение:  .
. существует, линейно и единственно.
существует, линейно и единственно. удовлетворяющему условию
удовлетворяющему условию  , являющийся образом g при отображение
, являющийся образом g при отображение  .—это значит определить его действие на произвольный вектор
.—это значит определить его действие на произвольный вектор  .
. на произвольный вектор
на произвольный вектор  . Затем вычисляем значение заданного функционала
. Затем вычисляем значение заданного функционала  . Т.к. выполняются эти условия:
. Т.к. выполняются эти условия: 
 , то можем утверждать, что данное отображение будет линейным.
, то можем утверждать, что данное отображение будет линейным.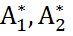 -- два отображения, для которых справедливо
-- два отображения, для которых справедливо  для всех
для всех 
 |u>=0. Фиксируем g и будем менять u. Тогда элемент (
|u>=0. Фиксируем g и будем менять u. Тогда элемент ( . Как линейная функция на
. Как линейная функция на  принимает только нулевые значения, и, значит, равен нулю. Поэтому
принимает только нулевые значения, и, значит, равен нулю. Поэтому  , что доказывает единственность и завершает доказательство теоремы.
, что доказывает единственность и завершает доказательство теоремы. - биортогональные базисы пространства
- биортогональные базисы пространства  . Тогда если отображение А в базисах Е и Н имеет матрицу А, то сопряженное отображение
. Тогда если отображение А в базисах Е и Н имеет матрицу А, то сопряженное отображение  .
.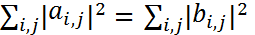


 :
: A(x + y) = (
A(x + y) = ( Ax +
Ax +  Ay) + (
Ay) + ( , y =
, y =  (
( A
A  +
+  A
A  =
=  +
+  ∈ R ⇒ Im
∈ R ⇒ Im  = Re
= Re  , где U ∈
, где U ∈  - унитарная матрица, Λ = diag{
- унитарная матрица, Λ = diag{  ,..,
,..,  }∈
}∈  ,
,  =
=  =
=  :
:  = (
= ( ). Тогда
). Тогда


 и диагональная матрица
и диагональная матрица  , что
, что  . При любом векторе
. При любом векторе  верны равенства
верны равенства 
 неотрицателен, поэтому
неотрицателен, поэтому



 из правой части соотношения (2) имеем:
из правой части соотношения (2) имеем: 
 . Следовательно,
. Следовательно,  .(5)
.(5)

 аналогичны.
аналогичны. , то существуют положительно полуопределенные эрмитовы матрицы H и K, однозначно определяемые матрицей A, и унитарные матрицы W и Y из
, то существуют положительно полуопределенные эрмитовы матрицы H и K, однозначно определяемые матрицей A, и унитарные матрицы W и Y из 
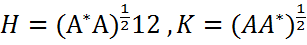 .
. (2),
(2),
 =, то верно и
=, то верно и  .
. .
. , наз. матричной нормой, если для любой A ∈
, наз. матричной нормой, если для любой A ∈  выполняются следующие условия:
выполняются следующие условия: A=0 (невырожденность);
A=0 (невырожденность); (абсолютная однородность);
(абсолютная однородность); (кольцевое свойство)
(кольцевое свойство) Столбцовая норма (1-норма),
Столбцовая норма (1-норма), Строчная норма (∞-норма),
Строчная норма (∞-норма), Евклидова норма
Евклидова норма Спектральная норма
Спектральная норма М-норма
М-норма ≡
≡  l1-норма
l1-норма

 .
.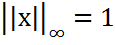 и точные равенства во всей цепочке выше.
и точные равенства во всей цепочке выше. подчиненная векторной норме ||•||∞
подчиненная векторной норме ||•||∞ (1)
(1)
 ||•||: ||A||<1
||•||: ||A||<1  .
. Ak→||•||0
Ak→||•||0  является сходящейся тогда и только тогда, когда
является сходящейся тогда и только тогда, когда  .
. .
. ||
|| 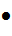 ||:||A||<1
||:||A||<1  Ak→k→∞0
Ak→k→∞0
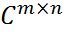 обозначим
обозначим  - строчная почти-нормы, а также
- строчная почти-нормы, а также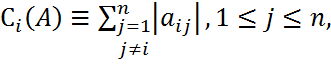 - столбцовые почти – нормы матр. А.
- столбцовые почти – нормы матр. А.

 .
.




 имеет собственные значения λ1,…,λn, то
имеет собственные значения λ1,…,λn, то
 , такая, что U*AU =T, где T – верхняя треугольная матрица с диагональными элементами tii=λi, i=1,n. Тогда
, такая, что U*AU =T, где T – верхняя треугольная матрица с диагональными элементами tii=λi, i=1,n. Тогда ,а значит
,а значит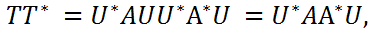 т.е. матрицыAA∗и TT∗подобны.
т.е. матрицыAA∗и TT∗подобны.
 , т.е. тогда итолько тогда, когдаматрицаA– нормальная.
, т.е. тогда итолько тогда, когдаматрицаA– нормальная. ,то
,то

 x*x.(2).
x*x.(2).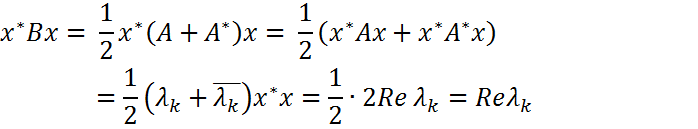


 все диагональные элементы ненулевые и она является матрицей с диагональным преобладанием, причем для всех, кроме одного, значений i=1,2,..,n это свойство выполняется в сильной форме, т.е. |aii|>Ri(A), то А обратима.
все диагональные элементы ненулевые и она является матрицей с диагональным преобладанием, причем для всех, кроме одного, значений i=1,2,..,n это свойство выполняется в сильной форме, т.е. |aii|>Ri(A), то А обратима.


 неразложима и A ≥ 0. Тогда
неразложима и A ≥ 0. Тогда ∈ σ(A);
∈ σ(A); ∈
∈  имеем
имеем  ;
; .
. ρ(B) − b ii.
ρ(B) − b ii. +
+ 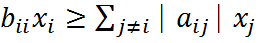 +
+  ⇒
⇒  ρ(B) -
ρ(B) -  , (i = ⌐ 1,n)
, (i = ⌐ 1,n) .
. , (i = ⌐1, n).По определению pij = λ−1
, (i = ⌐1, n).По определению pij = λ−1  a ij x i, и, следовательно
a ij x i, и, следовательно  , а значит, P — стохастическая.
, а значит, P — стохастическая. существует тогда и только тогда, когда A примитивна.
существует тогда и только тогда, когда A примитивна.


