
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегралы от экспоненты, умноженной на многочлен
Общее правило: за u всегда обозначается многочлен.
Пример 5 Найти неопределенный интеграл.
Решение:
Используя знакомый алгоритм, интегрируем по частям:
Если возникли трудности с интегралом Единственное, что еще можно сделать, это «причесать» ответ:
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом или даже То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Пример 6 Найти неопределенный интеграл
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за u всегда обозначается многочлен. Пример 7 Найти неопределенный интеграл.
Интегрируем по частям:
Пример 8 Найти неопределенный интеграл
Это пример для самостоятельного решения.
Пример 9 Найти неопределенный интеграл
Еще один пример с дробью. Как и в двух предыдущих примерах за u обозначается многочлен.
Интегрируем по частям:
Пример 10 Найти неопределенный интеграл
Это пример для самостоятельного решения. Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за u всегда обозначается обратная тригонометрическая функция. Напоминаем, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи мы будем называть их «арками».
Пример 11 Найти неопределенный интеграл.
Решаем.
Интегрируем по частям:
Здесь интеграл Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять другие методы и приёмы решения.
Пример 12 Найти неопределенный интеграл
Это пример для самостоятельного решения.
И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для
Пример 13 Найти неопределенный интеграл
Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.
Решения и ответы:
Пример 3: Решение:
Пример 4: Решение:
Интегрируем по частям:
Пример 6: Решение:
Дважды интегрируем по частям:
Пример 8: Решение:
Интегрируем по частям:
Пример 10: Решение:
Интегрируем по частям: Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла
Похожим способом также решаются интегралы вроде Более подробно – см. Интегралы от тригонометрических функций.
Пример 12:
Интегрируем по частям:
Пример 13:
Интегрируем по частям:
Примечание: Если возникли трудности с интегралом
то следует посетить урок Интегрирование некоторых дробей.
Интегралы от тригонометрических функций. Примеры решений
На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно.
Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.
А сейчас нам потребуются Таблица интегралов, Таблица производных и Справочник тригонометрических формул. Все методические пособия можно найти на странице Математические формулы и таблицы. Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится. Но сначала о том, каких интегралов в данной статье нет. Здесь не найдется интегралов вида При нахождении интегралов от тригонометрических функций используется ряд методов, в том числе: - использование тригонометрических формул; - понижение степени подынтегральной функции (частный случай п.1); - метод замены переменной; - универсальная тригонометрическая подстановка (частный случай п.3). Следует отметить, что данное разделение весьма условно, поскольку очень часто все вышеперечисленные правила используются одновременно в одном примере.
Пример 1 Найти неопределенный интеграл.
Сначала полное решение, потом комментарии.
Используем формулу:
(1) Мы видим, что в подынтегральном выражении находится произведение двух функций. К сожалению, в интегральном исчислении нет удобной формулы для интегрирования произведения в виде В данном случае мы прерываем решение значком (2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла. Справка: При работе с тригонометрическими функциями следует помнить, что: Косинус – это четная функция, то есть
В рассматриваемом примере: Синус – функция нечетная:
(3) Под интегралами у нас сложные функции (косинусы не просто от x, а от сложного аргумента). Это простейшие из сложных функций, интегралы от них удобнее найти методом подведения под знак дифференциала. (4) Используем табличную формулу Готово.
Пример 2 Найти неопределенный интеграл
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 3 Найти неопределенный интеграл
Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.
(1) Используем тригонометрическую формулу (2) Подводим функцию под знак дифференциала. (3) Используем табличный интеграл
Пример 4 Найти неопределенный интеграл
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 5 Найти неопределенный интеграл
Сначала решение:
(1) Используем формулу
(2) Используем основное тригонометрическое тождество (3) Почленно делим числитель на знаменатель. (4) Используем свойство линейности неопределенного интеграла. (5) Интегрируем с помощью таблицы.
Пример 6 Найти неопределенный интеграл
Это пример для самостоятельного решения, полное решение и ответ – в конце урока. Также существуют интегралы от тангенсов и котангенсов, которые находятся в более высоких степенях.Интегралы от тангенса (котангенса) в четвертой и пятой степенях можно раздобыть на странице Сложные интегралы.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 539; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.69 (0.042 с.) |




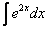 , то следует вернуться к статье Метод замены переменной в неопределенном интеграле.
, то следует вернуться к статье Метод замены переменной в неопределенном интеграле.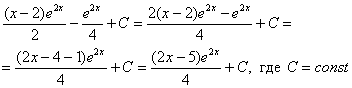
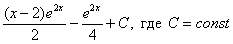 ,
, .
.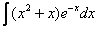 .
. – сложная функция.
– сложная функция.
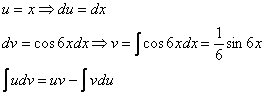

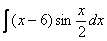 .
. .
.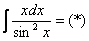
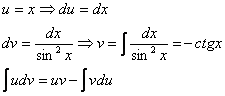

 .
.
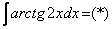 .
.

 найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример разбирался на уроке Метод замены переменной в неопределенном интеграле.
найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример разбирался на уроке Метод замены переменной в неопределенном интеграле. .
.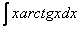 .
. .
.
 .
.


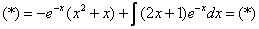

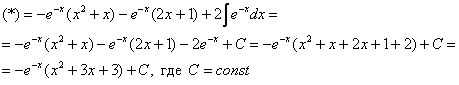
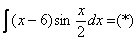
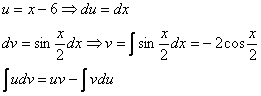

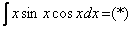
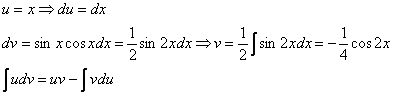

 . Её можно было использовать и сразу:
. Её можно было использовать и сразу: 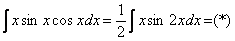 , а потом интегрировать по частям.
, а потом интегрировать по частям.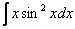 ,
,  – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул.
– в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул.


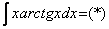


 ,
, ,
, 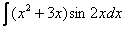 – косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений. Также здесь не найдется интегралов с «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.
– косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений. Также здесь не найдется интегралов с «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.
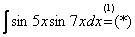


 , поэтому приходится прибегать к различным ухищрениям.
, поэтому приходится прибегать к различным ухищрениям. и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму.
и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму. , - минус исчезает без всяких последствий.
, - минус исчезает без всяких последствий. .
. , – здесь минус, наоборот, не пропадает, а выносится.
, – здесь минус, наоборот, не пропадает, а выносится. , единственное отличие в том, что вместо «икса» у нас сложное выражение.
, единственное отличие в том, что вместо «икса» у нас сложное выражение. .
. .
.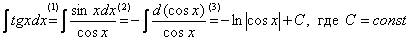
 .
.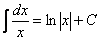 .
.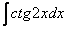 .
. .
.
 .
. , из которого следует, что
, из которого следует, что  .
. .
.


