
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множество геометрических векторов.
Вектором называется направленный отрезок или упорядоченная пара точек. Начало вектора также называется точкой его приложения. Замечание. Упорядоченным множеством называется множество элементов, взятых в определенном порядке. Обозначать векторы принято одним из следующих способов: Нулевым вектором или нуль-вектором называется вектор, начало и конец которого совпадают. Замечание. Направление нулевого вектора не определяется (считается произвольным). Нуль-вектор будем обозначать Длиной (модулем, абсолютной величиной) вектора называется расстояние между его началом и его концом. Обозначение: Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых. Иными словами, векторы коллинеарны, если существует прямая, которой они параллельны. Коллинеарность обозначается символом параллельности: Ненулевые коллинеарные вектора, могут быть: a) сонаправленными (имеющими одинаковое направление), что мы будем обозначать б) противоположно направленными (имеющими противоположное направление), что мы будем обозначать Замечание. Отметим очевидные свойства отношений сонаправленности и противоположно направленности: 1. Если 2. Если 3. Если 4. Если Векторы называются компланарными, если существует плоскость, которой они параллельны. Два вектора называются равными, если они коллинеарны, сонаправлены и имеют равные длины. Замечание 1. Все нулевые векторы равны между собой. Замечание 2. Введем понятия связанного, скользящего и свободных векторов. Связанным называется вектор, имеющий фиксированное начало и конец. Скользящим вектором называется множество всех связанных векторов, равных данному, начала которых расположены на одной и той же прямой. Свободным вектором называется множество всех связанных векторов, равных данному. Таким образом, скользящий вектор может быть перенесен вдоль прямой, на которой он лежит, а свободный вектор может быть отложен из любой заданной точки. Понятие свободного вектора является наиболее общим, так как любой связанный или скользящий вектор может быть представлен в виде разности двух свободных векторов.
Ортом, или единичным вектором, называется вектор, длина которого равна единице. Ортом вектора Углом между ненулевыми векторами называется угол между прямыми, на которых расположены данные векторы. Векторы, лежащие на перпендикулярных прямых, называются ортогональными. Вектор, имеющий одинаковый модуль с вектором
Линейными операциями над векторами назовем операции сложения двух векторов и умножения вектора на скаляр (число). Суммой Правила сложения векторов: а) Правило треугольника (Рис. 1)
б) Правило параллелограмма (Рис.2) Строим на векторах выходящая из общего начала векторов Замечание. Правило треугольника легко распространить на случай большего количества суммируемых векторов. В этом случае это правило называется правилом многоугольника (Рис. 3). Обозначим множество свободных векторов через Теорема. (Свойства операции сложения векторов) 1.
3. 4. Доказательство: 1. Рассмотрим сумму векторов
3. Третье свойство очевидно: 4. Пусть
Ч.т.д. Разностью Правило вычитания векторов. Разностью векторов
Замечание. Очевидно, что
Теорема. (Критерий коллинеарности двух векторов). Для того, чтобы два вектора Доказательство: Необходимость. Пусть Достаточность. Если Ч.т.д.
|
||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.210 (0.013 с.) |
 (А – начальная точка, В – конечная точка),
(А – начальная точка, В – конечная точка),  ,
,  , и т.д. Чтобы отличить векторную величину от скалярной величины, сверху используется черта (или стрелочка). Скалярной называется величина, характеризующаяся только своим численным значением (примеры: объем, температура, масса и т.д.). Для описания других объектов необходимо задавать не только их численное значение, но и направление (сила, скорость и т.д.); такие объекты называются векторными величинами.
, и т.д. Чтобы отличить векторную величину от скалярной величины, сверху используется черта (или стрелочка). Скалярной называется величина, характеризующаяся только своим численным значением (примеры: объем, температура, масса и т.д.). Для описания других объектов необходимо задавать не только их численное значение, но и направление (сила, скорость и т.д.); такие объекты называются векторными величинами.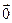 .
. . Естественно,
. Естественно,  .
. . Нуль-вектор коллинеарен любому другому вектору, так как он не имеет определенного направления:
. Нуль-вектор коллинеарен любому другому вектору, так как он не имеет определенного направления:  .
. ;
; .
. , то
, то  ;
; , то
, то  ;
; .
. . Если
. Если  , то
, то  .
. 2. Линейные операции над векторами.
2. Линейные операции над векторами. двух векторов
двух векторов  назовем вектор, идущий из начала вектора
назовем вектор, идущий из начала вектора  Вектор
Вектор  .
.

 2.
2. 
 (ассоциативность);
(ассоциативность);
 ;
; .
.
 2. Из Рис. 1.5.
2. Из Рис. 1.5.

 Положим
Положим  Тогда
Тогда 
 двух векторов
двух векторов  , для которого
, для которого  .
. .
. Произведением вектора
Произведением вектора  называется вектор
называется вектор  ;
; ;
; при
при 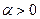 и
и  при
при  .
. , что
, что  .
. , где число
, где число  ; если
; если  . Очевидно,
. Очевидно,  , так как
, так как  и
и  . Таким образом, мы указали число
. Таким образом, мы указали число 


