
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема (о промежуточной последовательности).Стр 1 из 6Следующая ⇒
Доказательство. Рассмотрим а) б)
Замечание: Если в условиях леммы хотя бы один из концов исключить, то аналогичная лемма будет не верна.
0 1/3 1/2 1
БИЛЕТ 3. Предел числовой последовательности. Единственность предела. Ограниченность сходящейся последовательности. Определение: функцию
Определение: Число
Теорема: (о единственности предела): Если Доказательство: Пусть Для определенности
Противоречие.
Теорема: (об ограниченности сходящейся последовательности): Если
Возьмем Обозначим
Отсюда для обоих случаев
Замечание: обратное не верно.
БИЛЕТ 4. Свойства сходящихся последовательностей, связанные с неравенствами. Теорема: (о предельном переходе в неравенство): Пусть Замечание:
Доказательство (от противного): Пусть
Возьмем Обозначим
Замечание: Если для элементов последовательности выполняется
Теорема (о промежуточной последовательности). Пусть Замечание:
Доказательство:
Возьмем произвольный
Ограниченность.
+ Монотонность.
+
…
По теореме о монотонности последовательности
БИЛЕТ 9. Подпоследовательности. Частичные пределы. Теорема о частичных пределах сходящейся подпоследовательности.
Определение: Пусть дана некая последовательность
Замечание: Элементы подпоследовательности выбираются в порядке их следования в исходной последовательности.
Определение: Если
Теорема (о частичных пределах сходящейся подпоследовательности): Пусть
Доказательство: Возьмем произвольный Возьмем произвольную
Замечание: Понятие частичных пределов для сходящихся последовательностей не нужно.
БИЛЕТ 10. Теорема Больцано-Вейерштрасса. Теорема: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. Т.обр.
БИЛЕТ 13. Свойства пределов функций, связанные с неравенствами.
Теорема: Пусть Теорема: (Локальн. Огр.): Пусть
Возьмем
Теорема: Пусть Возьмем произвольный
Теорема: Пусть
Теорема (об отделимости от нуля): Пусть Доказательство:
Возьмем
БИЛЕТ 14. Теорема об арифметике пределов функций. Теорема: Если существуют 1). 2). 3). 4). Доказательства: Доопределив по непрерывности функции
1). 2). 3). 4).
Для доказательства возьмем вектор
Докажем, что ( А раз
Кроме того:
БИЛЕТ 16. Второй замечательный предел.
На первый взгляд кажется, что
Из этой таблицы видно, что с уменьшением
Доказательство: Рассмотрим этот предел, как предел функции натурального аргумента на бесконечность. Тогда: По определению Гейне:
Вычислим
По определению Гейне рассмотрим
То есть
БИЛЕТ 17. Сравнение бесконечно малых функций. Примеры.
Определение: Определение: Пусть 1) 2) ( 4). 5).
Примеры: 1). 2).
1 0 4).
5).
БИЛЕТ 18. Эквивалентные бесконечно малые функции. Критерий эквивалентности. Теорема о замене на эквивалентные.
Определение: функция Теорема (критерий эквивалентности): Пусть
Доказательства: (
то есть
(
Теорема (о замене на эквивалентные): Пусть функция
1 1
БИЛЕТ 19. Определения непрерывности функции в точке. Простейшие свойства непрерывных функций. Определение 1: Функция Определение 2: Функция Определение 3: Функция
Свойства непрерывных функций:
Теорема 1 (локальная огр.): Пусть функция
Теорема 2 (отделимость от 0): Пусть функция
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.118.250 (0.198 с.) |
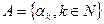 ,
, 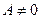 ,
, 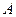 ограничено сверху, так как любое
ограничено сверху, так как любое 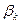 является верхней границей множества
является верхней границей множества 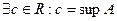 . Тогда:
. Тогда: - верхняя граница
- верхняя граница 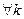
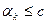 .
.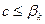 .
.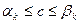 .
.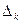
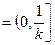 .
. (] ] ] ]
(] ] ] ]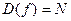 называют числовой последовательностью.
называют числовой последовательностью.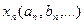 - члены числовой последовательности.
- члены числовой последовательности. - номер члена числовой последовательности.
- номер члена числовой последовательности.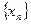 или
или 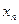 ,
, 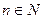
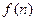 ,
, 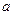 называется пределом последовательности
называется пределом последовательности 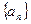 (пишут
(пишут 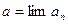 ), если для любого положительного числа
), если для любого положительного числа  (
(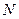 , зависящее от
, зависящее от 
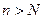 .
.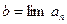 ,
, 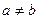 .
.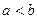 имеем:
имеем: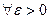

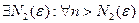
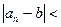
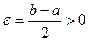
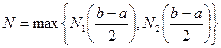
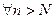 .
.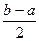
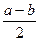 <
< 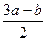 <
< 
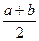 .
. 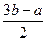 .
.
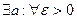
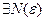 :
: 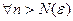

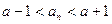 .
.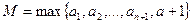 , тогда
, тогда 
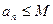
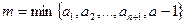 , тогда
, тогда 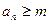
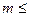
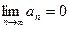 ,
, 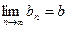 .
. 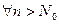
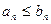 . Тогда
. Тогда 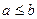 .
.
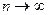
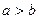 .
.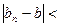
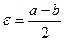 .
.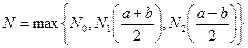
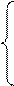
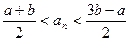
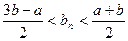
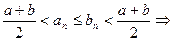
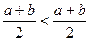 - противоречие.
- противоречие.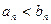 , то отсюда не следует, что
, то отсюда не следует, что 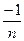 ,
, 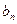 =
= 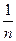 ,
, 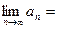
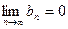 .
.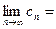
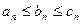 . Тогда существует
. Тогда существует 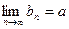 .
.
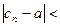
 .
.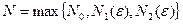 . Тогда
. Тогда 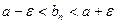 . (
. (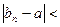
 -биноминальный коэффициент.
-биноминальный коэффициент.


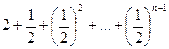 <
< 
 .
.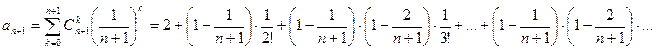


 .
. . Из элементов этой последовательности извлечем другую последовательность
. Из элементов этой последовательности извлечем другую последовательность  , где последовательность
, где последовательность  -номера элементов исходной последовательности, причем
-номера элементов исходной последовательности, причем  Тогда последовательность
Тогда последовательность  - подпоследовательность последовательности
- подпоследовательность последовательности  .
. , то
, то  , тогда
, тогда 

 .
. . Тогда
. Тогда  имеем:
имеем:
 . Таким образом:
. Таким образом:

 ., то есть
., то есть 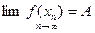
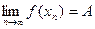 и
и  , тогда
, тогда 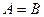 .
.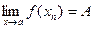 , тогда
, тогда  ,
,  :
: 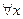
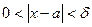
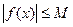 .
.
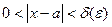
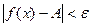 .
. Тогда
Тогда 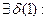
 .
.


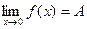 ,
, 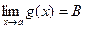 и
и 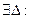
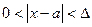
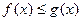 . Тогда
. Тогда 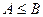
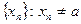 ,
, 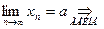
 ,
, 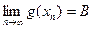 , причем
, причем 
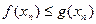 .
.
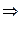 (по теореме о предельном переходе в неравенство)
(по теореме о предельном переходе в неравенство)  ,
, 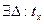
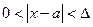
 . Тогда существует
. Тогда существует  . Возьмем произв.
. Возьмем произв. 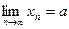

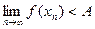 ,
, 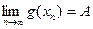 , причем
, причем 
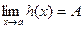 .
.
 , тогда
, тогда 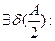
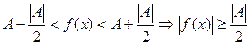 ,
, 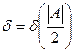 ,
, 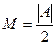 .
.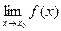 и
и  , то:
, то: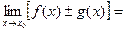
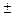
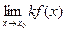 =
= 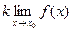 (
(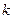 - постоянная).
- постоянная).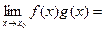
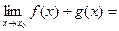
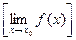
 , если
, если  .
.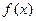 и
и 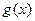 в точке
в точке  , положив
, положив 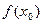 =
= 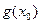 =
= 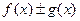 ,
, 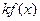 ,
, 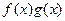 ,
, 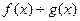 (так как
(так как 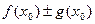 =
= 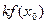 =
= 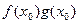 =
=  =
= 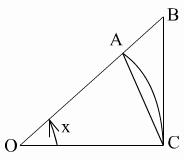 БИЛЕТ 15. Первый замечательный предел.
БИЛЕТ 15. Первый замечательный предел.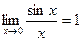
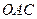 окружности радиуса 1 с центральным углом, равным
окружности радиуса 1 с центральным углом, равным  (радиан),
(радиан),  и проведем
и проведем 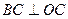 . Тогда пл.
. Тогда пл. 
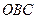 или
или 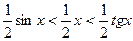 . Разделив все части этого неравенства на
. Разделив все части этого неравенства на 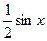 > 0, получим
> 0, получим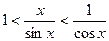 или
или  . Это неравенство, доказанное для любых
. Это неравенство, доказанное для любых 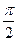 ), верно для любого
), верно для любого  из интервала (-
из интервала (- 
 ) при
) при 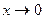
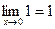 , то
, то  =
= 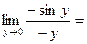 1
1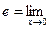
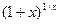 .
.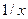 возводится 1+
возводится 1+ 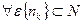
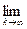
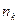 =
= 
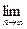
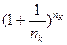 =
= 

 =
= 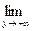
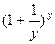 .
.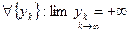 .
.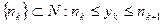


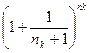


 *
* 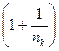
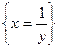 =
= 
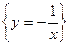 =
=  =
= 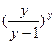 =
= 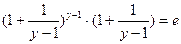
 бесконечно малая функция при
бесконечно малая функция при 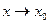 , если
, если 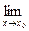
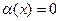 .
.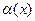 и
и 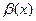 - бесконечно малые функции при
- бесконечно малые функции при 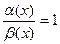 .
.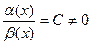 . 3)
. 3) 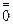 (
( .
. .
.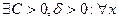

 .
. при
при 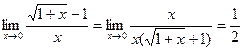 (
(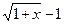 ,
, 
 3).
3). 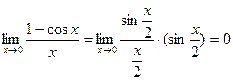 (
(
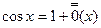 )
) (
(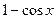 )- 2-й порядок малости относительно
)- 2-й порядок малости относительно 
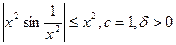 - произвольная.
- произвольная.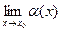 =0.
=0.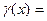
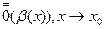 .
.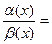
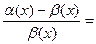
 =0,
=0,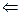 ).
). 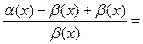
 =1.
=1.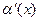 ,
,  при
при 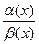 , тогда существует и
, тогда существует и  =
= 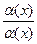 *
* 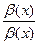 =
= 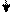
 .
.
 ,
,  .
.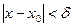
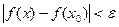 .
.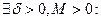

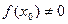 , тогда
, тогда


