
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Интегральное исчисление ⇐ ПредыдущаяСтр 4 из 4
Разберите решение задачи 7 данного пособия.
Задача 7. Найти интегралы: а) Решение:
а) В этом интеграле сделаем замену переменной
б) В этом случае необходимо применить формулу интегрирования по частям:
Применение формулы интегрирования по частям, даст возможность понизить показатель степени степенной функции.
в) Запишем подынтегральную функцию в виде суммы простейших дробей, имеем
или после приведения выражения правой части к общему знаменателю:
Полученное равенство выполняется тождественно (т.е. при любых значениях переменной x), только если
Приравняем коэффициенты при переменных в левой и в правой части равенства, получим
Используя найденное представление для подынтегральной функции, имеем:
Вопросы для самопроверки 1. Понятие неопределенного интеграла. 2. Первообразная функция. 3. Основные свойства неопределенного интеграла. 4. Таблица основных формул интегрирования. 5. Независимость вида неопределенного интеграла от выбора аргумента. 6. Свойства неопределенного интеграла. 7. Основные методы интегрирования. 8. Непосредственное интегрирование. 9. Метод разложения. 10. Метод замены переменной. 11. Метод интегрирования по частям. 12. Интегрирование рациональных дробей и тригонометрических функций. 13. Интегрирование некоторых видов иррациональностей.
Тема 7. Ряды
Разберите решение задачи 8 данного пособия.
Задача 8. Написать первые три члена ряда
найти интервал сходимости ряда и исследовать его сходимость на концах интервала. Решение: Беря последовательно
Для нахождения области сходимости ряда применим признак Даламбера
Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству
Исследуем сходимость ряда на концах полученного интервала. При
Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при Пусть
Исследуем сходимость этого ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл
Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при Таким образом,
Вопросы для самопроверки 1. Что называется числовым рядом? 2. Что называется n-ой частичной суммой числового ряда? 3. Какой числовой ряд называется сходящимся? 4. Что является необходимым условием сходимости числового ряда? 5. Назовите достаточные признаки сходимости, основанные на сравнении рядов. 6. Назовите признак Даламбера сходимости рядов. 7. В чем состоит интегральный признак сходимости Коши? 8. Какие ряды называются знакочередующимися? Приведите примеры. 9. Сформулируйте признак Лейбница сходимости знакочередующихся рядов. 10. Какие знакочередующиеся ряды называются абсолютно сходящимися? Условно сходящимися? 11. Дайте определение степенного ряда и области его сходимости. 12. Как найти область сходимости степенного ряда?
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.168 (0.005 с.) |
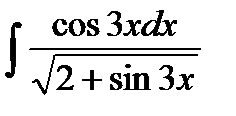 ; б)
; б)  ; в)
; в) 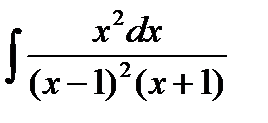 .
. Возвращаясь к исходной переменной, окончательно имеем:
Возвращаясь к исходной переменной, окончательно имеем: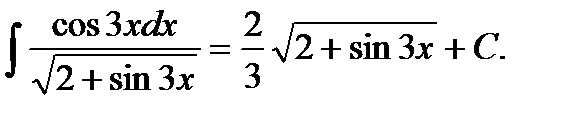

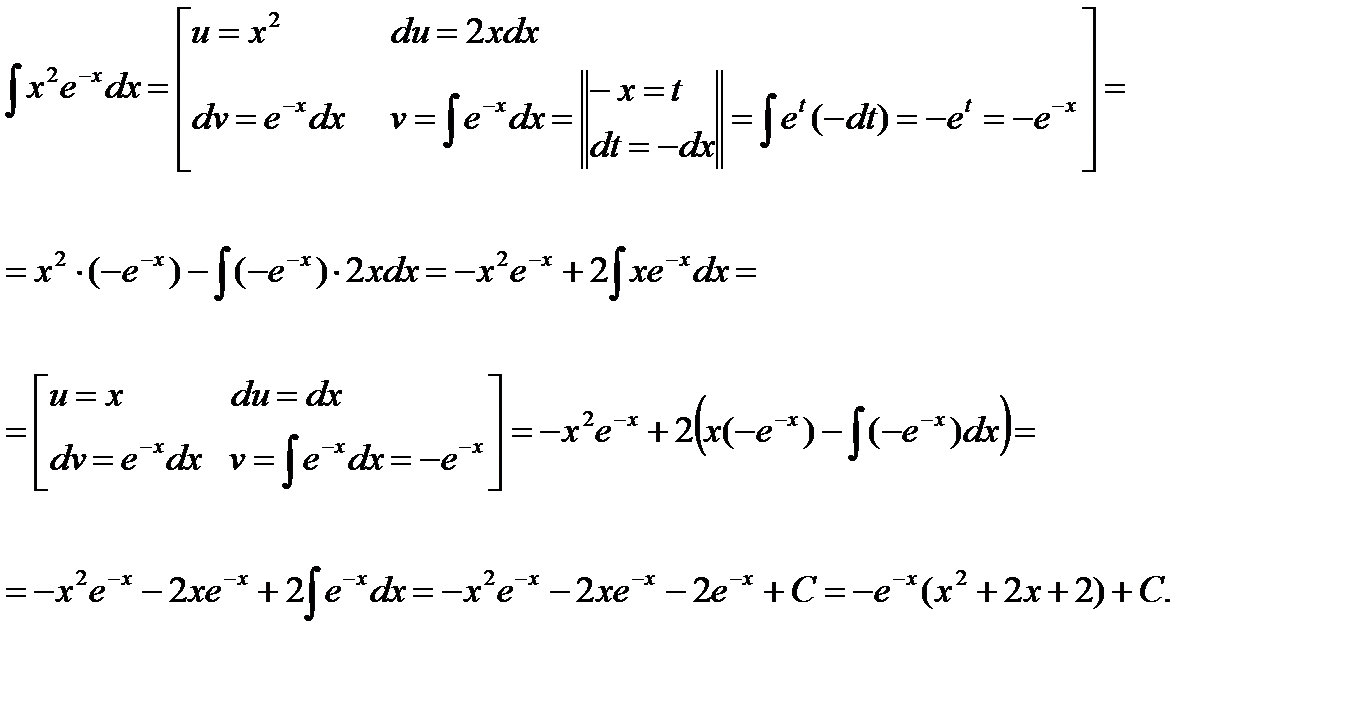
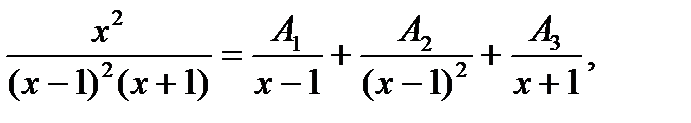





 , запишем данный ряд в виде:
, запишем данный ряд в виде:


 данный ряд принимает вид
данный ряд принимает вид
 . Следовательно, по признаку Лейбница сходимости знакочередующихся рядов, этот ряд сходится. Значит,
. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов, этот ряд сходится. Значит,  . Тогда заданный ряд примет вид
. Тогда заданный ряд примет вид

 – область сходимости данного ряда.
– область сходимости данного ряда.


