
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение и основные возможности программного пакета MathCAD.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Назначение и основные возможности программного пакета MathCAD. Mathcad - это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования. Название системы происходит от двух слов -MATHematica (математика) и CAD (Computer Aided Design — системы автоматизированного проектирования, или САПР). Так что вполне правомерно считать Mathcad математическими САПР. Основные возможности Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие. Среди возможностей Mathcad можно выделить: — Решение дифференциальных уравнений, в том числе и численными методами — Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.) — Использование греческого алфавита как в уравнениях, так и в тексте — Выполнение вычислений в символьном режиме — Выполнение операций с векторами и матрицами — Символьное решение систем уравнений — Аппроксимация кривых — Выполнение подпрограмм — Поиск корней многочленов и функций — Проведение статистических расчётов и работа с распределением вероятностей — Поиск собственных чисел и векторов — Вычисления с единицами измерения — Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров — С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.
Из чего состоит библиотека встроенных функций. Мощная библиотека встроенных функций позволяет решать широкий круг инженерных и математических задач:
Типы данных. Наиболее простой и распространенный ввод-вывод данных в MathCAD реализован присваиванием и выводом (либо численным, либо символьным) непосредственно в документе. Переменные и функции, посредством которых осуществляется ввод-вывод, могут иметь значения различных типов (числовые, строковые и т. д.). Перечислим основные типы данных, которые обрабатываются процессорами системы MathCAD: Для ввода числа в других системах счисления: двоичной (binary), восьмеричной (octal) или шестнадцатеричной (hexadecimal), сделайте следующее: 4.1.2. Комплексные числа 4.1.3. Встроенные константы
Массивы в Mathcad Столбец чисел называется вектором, а прямоугольная таблица чисел - матрицей. Общий термин для вектора или матрицы - массив. При работе с матрицами используется панель инструментов “Матрицы”:
Действия с матрицами. Арифметические операции с матрицами производятся так же, как и с обычными переменными. Пусть даны две матрицы 5х4 -- B1 и B2. Чтобы сложить их, достаточно записать «B1 + B2» и символ «=». Аналогично производится вычитание и умножение.
Построение графика функции.
16. Решение уравнения с одним неизвестным: root(f(х),х); root(f(х),х,а,b). Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.
· f(x) — скалярная функция, определяющая уравнение f(x)=0; · х — имя скалярной переменной, относительно которой решается уравнение; · а, b — границы интервала, внутри которого происходит поиск корня.
Листинг 5.13. Два варианта уравнения методом секущих Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x),x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке. В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были "хорошими", т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение. Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной. Листинг 5.14. Пример уравнения, которое удается решить только методом секущих
Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой — как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки "This variable or function is not defined above", в данном случае говорящей о том, что другая переменная ранее не определена. ПРИМЕЧАНИЕ
Наложение связей.
Для выполнения этой операции во вкладке Назначение инструментальной панели с помощью кнопки Установка связей в узлах
Задание нагрузок. Функции задания нагрузок содержатся в разделе Загружения инструментальной панели. Режим задания нагрузок включает функции, обеспечивающие автоматическое формирование собственного веса конструкции, задание динамических и статических нагрузок различного вида на узлы и элементы схемы, сохранение назначенных нагрузок в виде схем загружений или групп нагрузок. Зададим нагрузки на учебную расчетную схему в виде двух загружений: Загружение 1 – описывает постоянную нагрузку на перекрытиях и покрытиях и собственный вес колонн, которые задаются как равномерно распределенная нагрузка на ригели – 4.36 т/м, и равномерно распределенная нагрузка на колонны – 0.66 т/м. Нагрузки задаются по направлению оси Z общей системы координат; Загружение 2 – описывает временную с пониженным нормативным значением нагрузку. Задается аналогично загружению 1, но с другими значениями нагрузок – соответственно 3.57 и 0.54 т/м. Для задания этих нагрузок воспользуемся следующими кнопками инструментальной панели:
Для ввода нагрузок необходимо выполнить следующие операции:
Если активизировать фильтр отображения распределенных нагрузок, то введенные нагрузки будут показаны на расчетной схеме. При включенном фильтре визуализации значений нагрузки рядом с нагрузкой будет показано ее значение. Для записи загружения надо нажать кнопку в инструментальной панели. В диалоговом окне Сохранить загружение ввести имя загружения и нажать кнопку ОК. Ввод имени не является обязательным, но эта информация позволяет лучше ориентироваться при анализе исходных данных и результатов расчета. Номер загружению будет присваивается автоматически (с согласия пользователя), о чем сообщается в специальном окне. Перед тем, как ввести следующее загружение, воспользуйтесь операцией – очистка текущего загружения. При ее выполнении происходит очистка схемы от нагрузок текущего загружения. После этого можно готовить новое загружение. Если при записи загружения ему присвоить номер ранее созданного, то оно будет записано вместо него.
Раздел Деформации. В этом режиме предусмотрено выполнение следующих функций отображения результатов: – вывод деформированной схемы на фоне исходной; – вывод деформированной схемы; – вывод значений перемещений по заданному направлению в узлах расчетной схемы; – цветовое отображение значений перемещений по заданному направлению в узлах расчетной схемы; – отображение исходного состояния схемы; – отображение на проекциях деформированной схемы на фоне исходной; – вывод изополей перемещений для пластинчатых элементов; – вывод изополей и изолиний перемещений для пластинчатых элементов; – вывод изолиний перемещений для пластинчатых элементов; – установка параметров цветовой шкалы; – отображение приведенных узловых масс; – формирование видеоклипов перемещений для статических и динамических загружений; – анимация перемещений для статических и После линейного расчета открываем в дереве проекта раздел Результаты, а в нем подраздел «Графический анализ». В открывшемся окне открываем инструментальную панель Деформации и нажимаем кнопку «Совместное отображение исходной и деформированной схемы». Рядом с исходной схемой появится картина деформированной схемы (без указания численных значений перемещений узлов). Для получения численных значений перемещений необходимо нажать кнопку «Вывод значений перемещений в узлах» или в дереве проекта нажать кнопку Печать таблиц. Откроется окно, с помощью которого надо открыть таблицу перемещений в узлах сетки элементов. Затем переходим в раздел Поля напряжений и на инструментальной панели этого раздела выбираем вариант изображения картины напряженного состояния балки - стенки.
Кнопки Параметры вывода. Для назначения правил формирования и оформления результатов используется кнопка Параметры вывода, после нажатия которой появляется диалоговое окно Состав выходных таблиц. Из этого окна осуществляется доступ к следующим функциям назначения параметров: • список узлов или элементов, для которых выводятся результаты; • список загружений; • параметры настройки генератора таблиц; • выходные единицы измерения. Параметры настройки задаются в диалоговых окнах, вызов которых выполняется нажатием соответствующих кнопок. В окне Параметры вывода, которое вызывается после нажатия одноименной кнопки, можно назначить количество строк на странице и ширину таблиц, точность вывода перемещений и усилий, выбрать тип таблицы, определить формат выходного файла, ориентацию страниц, размер шрифта и др. Есть два типа таблиц. В таблицах первого типа (их опция помечена в окне пиктограммой) наименования силовых факторов или перемещений размещены в начале каждой строки, а в заглавиях столбцов помещены номера узлов или элементов. В таблицах второго типа (отмеченных пиктограммой) в заглавиях столбцов помещаются наименования силовых факторов или перемещений, а в строках - номера элементов и узлов. Используя соответствующую маску вывода, можно настроить программу на печать только определенных видов силовых факторов или перемещений.
Назначение и основные возможности программного пакета MathCAD. Mathcad - это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования. Название системы происходит от двух слов -MATHematica (математика) и CAD (Computer Aided Design — системы автоматизированного проектирования, или САПР). Так что вполне правомерно считать Mathcad математическими САПР. Основные возможности Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие. Среди возможностей Mathcad можно выделить: — Решение дифференциальных уравнений, в том числе и численными методами — Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.) — Использование греческого алфавита как в уравнениях, так и в тексте — Выполнение вычислений в символьном режиме — Выполнение операций с векторами и матрицами — Символьное решение систем уравнений — Аппроксимация кривых — Выполнение подпрограмм — Поиск корней многочленов и функций — Проведение статистических расчётов и работа с распределением вероятностей — Поиск собственных чисел и векторов — Вычисления с единицами измерения — Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров — С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.
|
||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 5060; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |















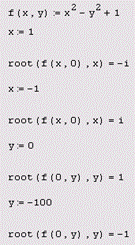
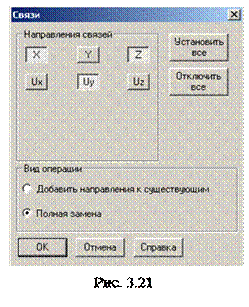 Наложение связей в опорных узлах
Наложение связей в опорных узлах вызываем диалоговое окно Связи. В режиме Полная замена активизируем кнопки X, Z, UY (рис. 3.21) и нажимаем кнопку OK. Выделяем курсором на схеме узлы: 1, 2 и нажимаем кнопку Подтверждение
вызываем диалоговое окно Связи. В режиме Полная замена активизируем кнопки X, Z, UY (рис. 3.21) и нажимаем кнопку OK. Выделяем курсором на схеме узлы: 1, 2 и нажимаем кнопку Подтверждение  инструментальной панели, которая обеспечивает жесткое защемление опорных узлов 1 и 2 рамы в плоскости XоZ. Подобную операцию повторяем для шарнирно-неподвижного узла 3 (активизацией кнопок X, Z). Визуальный контроль правильности постановки опорных связей выполняем нажатием кнопки Связи
инструментальной панели, которая обеспечивает жесткое защемление опорных узлов 1 и 2 рамы в плоскости XоZ. Подобную операцию повторяем для шарнирно-неподвижного узла 3 (активизацией кнопок X, Z). Визуальный контроль правильности постановки опорных связей выполняем нажатием кнопки Связи  на панели Фильтры отображения.
на панели Фильтры отображения.


