
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування ройових алгоритмів для розв’язування екстремальних задачСтр 1 из 3Следующая ⇒
Застосування ройових алгоритмів для розв’язування екстремальних задач Роботу виконав: Клименко Кирил Володимирович, учень 10 класу Черкаського фізико- математичного ліцею(ФІМЛІ) Науковий керівник: Тріус Юрій Васильович, завідувач кафедри комп`ютерних наук та інформаційних технологій управління Черкаського державного технологічного університету, професор, доктор педагогічних наук
Черкаси – 2016
Застосування ройових алгоритмів для розв’язування екстремальних задач Клименко Кирил Володимирович Черкаське територіальне відділення МАН України Черкаський фізико-математичний ліцей (ФІМЛІ), 10 клас, м. Черкаси Науковий керівник: Тріус Юрій Васильович, завідувач кафедри комп`ютерних наук та інформаційних технологій правління Черкаського державного технологічного університету, професор, доктор педагогічних наук
В наш час в науці і техніці існує потреба вирішення широкого спектра завдань оптимізаційного характеру. Але далеко не всі з цих задач можуть бути вирішені з використанням традиційних підходів через відсутність необхідної інформації. Особливо складно піддаються рішенню ті завдання, які, як правило, представляють суттєвий інтерес у сенсі їх практичного застосування і характеризуються наступними математичними властивостями: необхідністю пошуку глобального оптимуму; складним ландшафтом поверхні пошук, багатомірністю, багатоекстремальністю, багатокритеріальністю завдань з обмеженнями; та багато іншими. Метою роботи є дослідження методу ройових алгоритмів, їх практичне застосування для розв’язку оптимізаційних задач і проблем, в основі яких лежать задачі оптимізації, моделювання і реалізація розв’язку в комп’ютерному середовищі Висновок: …
ЗМІСТ ВСТУП……………………………………………………………………………. РОЗДІЛ 1. ЗАГАЛЬНА ХАРАКТЕРИСТИКА РОЙОВИХ АЛГОРИТМІВ ТА ЇХ ЗАСТОСУВАННЯ……………………………………… 1.1. Загальна характеристика ройових алгоритмів……………………… 1.2. Огляд ройових алгоритмів…………………………………………… 1.3. Застосування ройових алгоритмів до розв’язування задач оптимізації…………………………………………………………...
РОЗДІЛ 2. КАНОНІЧНИЙ РОЙОВИЙ АЛГОРИТМ
ТА ЙОГО МОДИФІКАЦІЇ………………………………………………………. 2.1. Канонічний ройовий алгоритм для задач неперервної оптимізації……………………………………………………... 2.2. Адаптивний ройовий алгоритм. ………………………… 2.3. Реалізація ройових алгоритмів у пакеті Mathcad……….
РОЗДІЛ 3. Чисельний експеримент з перевірки результативності ройових алгоритмів для розв’язування задач оптимізації………………………………………………. ВИСНОВКИ………………………………………………………………... СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ………………………………….
ВСТУП В наш час досить актуальними є методи розв’язку задач, в яких недостатньо інформації для вирішення класичними методами або початкові умови яких невідомі чи зазнають постійних змін, для вирішення важливих глобальних проблем оптимального пошуку. Одними з таких алгоритмів є еволюційні алгоритми, зокрема і ройові. Такі алгоритми засновані на імітації явищ природи і реалізують адаптивний випадковий пошук. Ройові алгоритми широко застосовується також в задачах машинного навчання(зокрема, для навчання нейромереж та розпізнавання зображень), параметричної і структурної оптимізації (форм, розмірів і топологій) в області проектування, біохімії і біомеханіки. По ефективності він може змагатися з іншими методами глобальної оптимізації, а низька алгоритмічна складність сприяє простоті його реалізації. Метою роботи є дослідження методу ройових алгоритмів, їх практичне застосування для розв’язку оптимізаційних задач і проблем, в основі яких лежать задачі оптимізації, моделювання і реалізація розв’язку в комп’ютерному середовищі Mathcad та Matlab. Об’єктом дослідження є використання ройових алгоритмів для розв’язку задач в реальних умовах. Предметом дослідження є інтерпретація реальної задачу на математичку, розв’язок ройовими алгоритмами та зворотна інтерпретація рішення в реальні умови.
Огляд ройових алгоритмів Ройові алгоритми(PSO алгоритми) характеризуються стохастичністю, тобто кожен агент цієї системи в кожній наступній ітерації рухається випадково. Рух всього рою слід розглядати, як окремий рух кожного агента, знаходження найбільш оптимального значення під час кожної ітерації(локального мінімуму), а загальний процес являє собою аналіз кожним агентом отриманої інформації про оптимальне місцезнаходження кожного з усіх інших агентів. Такий процес можна визначити як взаємоаналіз, де кожна частка отримує вигоду з дослідів і попереднього досвіду всіх інших часток. Таким чином, цей алгоритм має найбільше шансів на отримання переваги над іншими алгоритмами, особливо коли оптимум невідомий, або розташований випадково.
Задачу оптимізації можна сформувати як пошук глобального екстремуму(мінімуму чи максимуму) цільової функції f(X), визначеній на проміжку D: f(X) → min(max), X∈D = { x ∈ Rd}, де область D – суттєвий гіперкуб з розмірністю d, X – векторний аргумент функції f, що оптимізується, а її глобальний розв’язок знаходиться в точці X* В цьому алгоритмі, сукупність часток представлена сукупністю точок-рішень, що рухаються у просторі в пошуку глобального оптимуму. Під час руху кожна частка обмінюється інформацією з сусідніми агентами і намагається покращити свій результат. Позначимо сукупність часток рою через
X = { x 1, x 2,…, x s}, де s – кількість елементів рою. I-та позиція позначає сукупність ії координат(xi1,xi2,…,xid), в d-розмірному просторі. Практично доведено, що найбільш раціонально використовувати 20-30 часток. На початковому етапі алгоритму відбувається ініціалізація рою часток. Якщо ж інформація про початкові дані про цільову функцію, то доцільно визначити за формулою
xij = rand(xj min, xj max), де xi,j – i-та частка j-ої координати(розмірності), rand(xj min, xj max) – випадково згенероване число в інтервалі [ xj min, xj max] j-ого простору, рівномірно розподілені на всьому інтервалі. Очевидно, що частки певним чином змінюють своє положення в просторі, тобто рухаються. Такий рух можна описати масивом V ={ v 1, v 2,…, v s}, де vs – вектор переміщення для s-ої частки. Такі вектори на початку можна вважати нульовими, але досвід встановив, що краще їх розраховувати по формулі
vi,j=[rand(xjmin,xjmax)-xi,j]/2, де vi,j – j-ий вектор руху i-ї частки. Такий спосіб гарантує, що під час завдання наступного вектора частки не вийдуть за межі пошуку. На наступних ітерація вектори розраховуються по формулі V’i,j = wvi,j + c1r1(pi,j – xi,j) + c2r2 (gj – xi,j), а наступна координата(позиція) кожної частки за формулою x’i,j = xi,j + v’i,j, де v'i x'I - новий вектор і положення і-ії частки; pi – найкраще положення, визначене попередньо(personal best); g – найкраще рішення, знайдене всім роєм(global best); w – інерційний коефіцієнт; c1,c2 - відповідно когнітивний і соціальні коефіцієнти; - випадкові числа, r1,r2 - генеровані випадково на інтервалі [0;1] для кожної координати. Якщо ж під час виконання частка виходить за межі простору пошуку, то її відповідний вектор набуває нульового значення, а частка отримує відповідно граничні координати, тобто переходить на край “поля” пошуку. Інерційний коефіцієнт w визначає вплив попереднього вектору частки на її нове значення. Величина коефіцієнта c1 показує ії індивідуальну поведінку і “прагнення” рухатися до напрямку найкращого рішення, знайденого нею до цього. Коефіцієнт c2 задає ступінь її колективної реакції і прагнення рухатися в напрямку до найкращого колективного рішення
Задач оптимізації
Ройові алгоритми, як вже було сказано, призначені для розв’язку задач оптимізації, або задач пошуку екстремуму(мінімального чи максимального значення). Одними з таких задач є задачі міжгалузевого балансу(МГБ). МГБ в економіці – це метод аналізу взаємозв’язків між різними галузями (секторами) економічної системи. При виробництві продукції (товарів, виконанні робіт та надання послуг) в кожній галузі споживається продукція, що виробляється у своїй та всіх інших галузях економіки. Це означає, що кожна галузь виступає в системі міжгалузевих відношень одночасно як виробник, так і як споживач. Мета міжгалузевого балансу – визначити, скільки продукції повинна виробити кожна галузь для того, щоб задовольнити всі потреби економічної системи в її продукції, тобто задовольнити як внутрішні потреби всіх галузей, так і потреби зовнішнього середовища (кінцевий попит: задоволення особистих потреб людей, суспільних потреб, накопичення продукції, експорт продукції). Сутність принципу балансу – все, що випускається (вал), дорівнює сумі витрат продукції на внутрішні потреби галузей економіки і випуск продукції для зовнішніх потреб (експорт): ВАЛ=ВИТРАТИ (ВНУТРІШНІ ПОТРЕБИ)+ВИПУСК (ЕКСПОРТ). Задача оптимізаційної ж задачі МГБ полягає у тому, щоб знайти вектор валової продукції X *, при якому досягається максимальний прибуток від накопиченої продукції Y* при відомій виробничій потужності галузей Математична модель МГБ Нехай в нас є n галузей, що виробляють продукцію, тоді A={ai,j} – матриця, що показує частку продукції, яка виробляється i-ю галуззю, що споживається j-ю галуззю i,j∈[1;n], X=(x1,x2,…,xn)T – вектор валової продукції, що показує загальну кількість виробленої продукції j-ї галузі, Y=(y1,y2,…,yn)T – вектор, що визначає замовлення на випуск готової продукції i-ю галуззю, що йде на експорт. Класична балансова задача ставить за мету визначити валовий випуск продукції всіх галузей (вектор Х), необхідний для: 1) задоволення внутрішніх потреб, що визначаються діючою технологією і, відповідно, матрицею А; 2) забезпечення замовлення на готову продукцію (вектор Y). Витрати на внутрішні потреби обчислюються як добуток матриці А на шуканий вектор Х:
випуск готової продукції визначається заданим вектором Y, тоді балансова модель визначається системою лінійних рівнянь: в матричному вигляді
або у розгорнутому вигляді
Таким чином, отримуємо, що X=(E-A)-1Y, де E – одинична матриця (n на n), усі елементи якої, крім головної діагоналі, нулі, а на головній діагоналі одиниці.
ТА ЙОГО МОДИФІКАЦІЇ Застосування ройових алгоритмів для розв’язування екстремальних задач Роботу виконав: Клименко Кирил Володимирович, учень 10 класу Черкаського фізико- математичного ліцею(ФІМЛІ) Науковий керівник: Тріус Юрій Васильович, завідувач кафедри комп`ютерних наук та інформаційних технологій управління Черкаського державного технологічного університету, професор, доктор педагогічних наук
Черкаси – 2016
|
||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.165.246 (0.029 с.) |

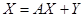 , (1.1)
, (1.1)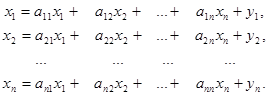 (1.2)
(1.2)


