
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение сочетаний. Сочетание можно интерпретировать Как размещение без повторений неразличимых предметов в ящиках.
Пример 1. Найдем вероятность угадать 7 номеров из 49 (игра спортлото). Количество вариантов равно числу сочетаний из 49 элементов по 7. Существует единственный благоприятный вариант. Отсюда вероятность равна Теорема 4. Число возрастающих функций f: {1, 2,×××, k } ® {1,2, ×××, n } равно Доказательство. Каждой возрастающей функции сопоставим ее образ { f (1), f (2), ×××, f (k)} Í {1,2, …, n }. Получим биекцию между возрастающими функциями и подмножествами множества {1, …, n }, состоящими из k элементов. Согласно определению сочетания, число таких подмножеств равно числу сочетаний Замечание. Возрастающая функция задается возрастающей последовательностью k чисел. Отсюда число возрастающих последовательностей x1 < …< xk чисел, принадлежащих множеству {1, 2, …, n }, будет равно Теорема 5. Число последовательностей натуральных чисел (x1, x2, ×××, xk), xi ³1, удовлетворяющих уравнению x1 + x2 + ××× + xk = n, равно Доказательство. Каждой последовательности (x1, x2, ×××, xk), удовлетворяющей данному уравнению сопоставим возрастающую последовательность y1 =x1 , y2 = x1+ x2, ×××, yk-1 = x1+ x2 +…+xk-1. Наоборот, каждой возрастающей последовательности y1 < …< yk-1 < n можно сопоставить решение данного уравнение, состоящее из чисел x 1= y 1, x 2= y 2- y 1, …, xk -1= yk -1- yk -2, xk = n-yk- 1. Получаем биекцию между решениями данного уравнения и возрастающими последовательностями, состоящими из k -1 чисел принимающих значения 1, 2, …, n-1. По теореме 4 число таких возрастающих последовательностей равно Теорема 6. Число неубывающих сюръекций {0,1, ×××, n –1} ® {0, 1, ×××, k–1 } равно Доказательство. Каждая сюръекция задает разбиение множества { 0, 1, ×××, k–1 } на подмножества f ─1(0), f ─1(1), ×××, f ─1(n –1). Пусть m0 – наибольший в f ─1(0), m1 – наибольший в f ─1(1), ×××, mn-2 – наибольший в f─1(n –2). Тогда mn-1 = k – 1. Следовательно, 0 ≤ m0 < m1 < ××× < mn-2 ≤ k-2. Число таких последовательностей равно Пример 2. Число неубывающих сюръекций n ® 1 равно Число неубывающих сюръекций 3 ® 2 равно Сочетания с повторениями. Сочетанием с повторением из множества { e1 , e2 , ×××, en } называется линейная комбинация x1e1 + x2e2 + ××× +xn en, состоящая из x1 элементов e1 , из x2 элементов e2 ,×××, из xn элементов en, где xi ≥ 0 – неотрицательные целые числа. Если x1 + ××× +xn = k, то оно называется сочетанием с повторениями из n по k.
Пусть, например, имеется 3 цвета: красный, зеленый, синий. Интенсивности этих цветов равны. Сколько смесей суммарной интенсивности 10 можно получить, смешивая x1 красных, x2 зеленых и x3 синих цвета? Лемма 1. Пусть Доказательство.

Каждому решению x1 + ××× +xn = k соответствует неубывающая последовательность y1 ≤y2 ≤ × × × ≤yn-1, где y1=x1, y2 = y1+x2, ×××, yn-1 = yn-2 + xn-1. Теорема 7. Доказательство. Рассмотрим график неубывающей функции
Рис. 2.3. График неубывающей функции График задается последовательностью из 0 и 1 0 0 1 1 0 0 … 0 1 0 0 … 1 1 … 1 состоящей из n-1+k разрядов, имеющих k единиц. Следствие 1. {1,2, ×××, k } ® {1,2, ×××, n }. Доказательство. Первый способ: транспонировать графики. Если график, показанный на рис.2.3, отразить относительно прямой y = x, то получим график функции {1,2, ×××, k } ® {1,2, ×××, n }. Это доказывает утверждение следствия. Второй способ: число неубывающих функций {1,2, ×××, k } ® {1,2, ×××, n } равно Получаем следующую таблицу 2.2, содержащую числа конфигураций Таблица 2.2 Число конфигураций
Здесь m = {0,1, ×××, m-1}. Например, число неубывающих сюръективных отображений {0,1, ×××, m -1} ® {0,1, ×××, n -1} равно
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.205.123 (0.007 с.) |
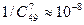 .
.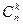 .
. .
. .
.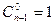 .
.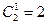 .
.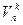 - число сочетаний с повторениями из n по k. Тогда
- число сочетаний с повторениями из n по k. Тогда 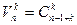 .
.
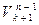 =
=  =
= 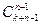 .
.

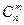
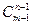
 .
.


