
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №2. Тема: свойства счетных множеств.
1. Всякое подмножество счетного множества: конечно или счетно. 2. Сумма конечного числа конечных (счетных) множеств есть конечное (счетное) множество. 3. Всякое бесконечное множество содержит хоть одно счетное подмножество.
Пусть существует множество M, имеется ряд подмножеств Булеан – это и есть множество всех подмножеств множества М.
Теория множеств строится на основе следующих аксиом:
1. Аксиома СУЩЕСТВОВАНИЯ: Существует по крайней мере одно множество. 2. Аксиома ОБЪЕМНОСТИ: Если два множества, составлены из одних и тех же элементов, то они равны (А = В). 3. Аксиома ОБЪЕДИНЕНИЯ: Для любых М,N существует R, элементами которого являются все элементы этих множеств, которые не содержат никаких других элементов. 4. Для любых M,N существует D, элементами которого являются те и только те элементы множества M, которые не являются элементами N. Множества часто задают графически с помощью диаграмм Эйлера-Венна, где всякий рассматриваемый контур соответствует одному из рассматриваемых множеств и ограничивает (символически) его элементы.
Операции над множествами
1. Включение M Каждый элемент множества М, обязательно принадлежит и множеству N, но не обязательно наоборот.
Объединение множества М и N, есть новое множество R, включающее в себя R все элементы обеих множеств.
M M(3,4,5)
N(3,4,5,6) Таким образом, произведением двух множеств, является множество R, элементы которого принадлежат к М и к N одновременно.
4. Вычитание: M\N: Разность множеств M и N это новое множество, К, элементы которого обладают свойствами М и не обладают свойствами N, т.е. принадлежат только множеству M.
5. Дополнение: Пусть имеется некоторое универсальное множество U и все рассматриваемые в нем множества есть его подмножества, тогда элементами множества
Лекции №3. Тема: основные тождества алгебры множеств.
1. 2.
3. 4.
5. 6.
7. 7а.
8. 9. 10. 11.
13. где Ø - пустое множество
Пример: M (1, 9, 12, 17, 33, 4, 16) N (33, 22, 45, 9, 1, 20, 35) 1. вычитание: R = (12, 17, 4, 16); 2. сложение: R = (1, 9, 12, 17, 33, 4, 16, 22, 45, 20, 35); 3. произведение: R = (1, 9, 33)
Лекция №4. Тема: кортежи. Происхождение от французского «торжественность».
Пусть М – конечное множество, элементами которого являются символы. Например: цифры, буквы. Кортеж – есть упорядоченный набор (строгая последовательность) элементов множества M. Алфавит - есть кортеж попарно различных символов, называемых буквами алфавита.
Рассмотрим множество состоящее из n элементов:0,1,2,…,n. Кортежи длины m из этих элементов, обозначим Mm, тогда мощность n(Mm), есть nm. Такие кортежи, которые называются упорядоченными наборами или векторами. Пример: M
Декартовое произведение множеств: Пусть заданы множества M1,M2,…. Mn. Декартовым произведением этих множеств называется множество состоящие из всех кортежей (m1, m2….mn) длины k1(mk Є Mk, M * M *… * M – nраз, обозначается как Mn и называется n – ой степенью M. Порядок задания множителей для декартового произведения, как для кортежей одинаков. Примерами декартовых произведений является таблица умножения, все возможные наборы пар координат на плоскости и т.д.
Пример: M1 = {0, 1, 2}, M2 = {x, y, z}, M3 = {A, Б, С} Декартовое произведение: M1 * M2 * M3
Отображения множеств (функций) Отображение f множества x во множество y – это когда каждому элементу x Є X, ставится в соответствие только один элемент y Є Y. Элемент y множества Y, соответствующий при отображении f элементу x из X называется образом элемента x. Если y = f(x), то x называется прообразом элемента y при этом отображении. Частный случай отображения множества X в Y имеет место, если каждый элемент множества Y имеет прообраз из множества X. В этом случае отображение (f) сюръективно, (может быть случай, когда несколько элементов Y имеют один и тот же прообраз в X).
Отображение f, называется инъективным, если для каждого элемента y Є Y существует не более 1- го прообраза, если отображение f сюръективно и инъективно, то оно называется биективным. Пример: функций, отображающих x Є R на множество y Є R на множество y Є R, где R – множество (бесконечное) действительных чисел.
1. f1(x) = Ex – инъективно (не сюръективно) 2. f2(x) = x*(x2-1) – сюръективно (не инъективно) 3. f3(x) = 3x+1 – биективно
Лекция №5. Тема: алгебра логики (булева алгебра).
В основе логико – математической теории дискретной математики лежит понятие: высказывание. Это повествовательное предложение, которое интересует математика прежде всего в узком смысле: истинно оно или ложно.
В алгебре логики основными связками (операциями) являются следующие: o дизъюнкция (или) o конъюнкция (и) o отрицание (не) o импликация (если…, то…) → o эквиваленция (тогда и только тогда, когда…) ↔ o штрих Шеффера (антиконъюнкция) | o стрелка Пирса (антидизъюнкция) ↓
При выполнении операций существует следующий порядок: - операции в скобках, если их нет тот операции выполняются так: I. отрицание II. конъюнкция III. дизъюнкция IV. импликация V. эквиваленция VI. штрих Шеффера VII. стрелка Пирса Конъюнкцией двух высказываний X, Y называется высказывание (функция) x
Дизъюнкция X и Y называется высказывание (функция) X
Импликацией X и Y называется высказывание (функция) X→Y, которая ложна тогда, и только тогда, когда X истинно, а Y ложно, и истинна в остальных вариантах.
Таблица истинности для импликации
Эквиваленцией X иY называется высказывание X↔Y, которое истинно тогда, и только тогда, когда X и Y оба истинны или ложны, одновременно.
Таблица истинности для эквиваленции
Штрих Шеффера (антиконъюнкция) - X│Y = X∩Y
____ Стрелка Пирса (антиконъюнкция) - X↓Y = XUY
____ Сложение по модулю два (антиэквиваленция) - X
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.195.204 (0.035 с.) |
 .
. N (mi Є M
N (mi Є M 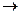 mi Є N)
mi Є N)
 - Диаграмма Эйлера-Венна
- Диаграмма Эйлера-Венна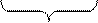 2. Объединение
2. Объединение 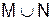 (cложение) M N
(cложение) M N M(1,2,3)
M(1,2,3) N
N 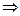 R (1,2,3,4,5)
R (1,2,3,4,5) 3. Произведение (пересечение): M
3. Произведение (пересечение): M  N
N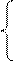 M(1,2,1,3,4)
M(1,2,1,3,4)
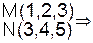 R(1,2)
R(1,2)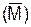
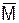 являются все элементы не входящие в М, но принадлежащие U, т.е. U без М есть множество
являются все элементы не входящие в М, но принадлежащие U, т.е. U без М есть множество 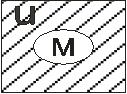



 Коммутативность
Коммутативность

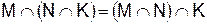 Ассоциативность
Ассоциативность

 Дистрибутивность
Дистрибутивность Закон
Закон Де Моргана
Де Моргана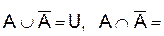 Ø
Ø  Ø
Ø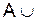 Ø
Ø 

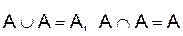
 Ø = Ø
Ø = Ø 12.
12.  Закон
Закон поглощения
поглощения (1,2,3,4), M
(1,2,3,4), M  (4,3,2,1) M
(4,3,2,1) M  (1,3,2,4); M
(1,3,2,4); M  1 ≤ k ≤ n), где m1Є M1, m2 Є M2, … mn Є Mn. Обозначается как M1*M2*…Mn. Произведение –
1 ≤ k ≤ n), где m1Є M1, m2 Є M2, … mn Є Mn. Обозначается как M1*M2*…Mn. Произведение – K1 = {(0, 1), (x, y), (A, Б)}, или К2 = {(1, 2), (x, z), (A, C)}.
K1 = {(0, 1), (x, y), (A, Б)}, или К2 = {(1, 2), (x, z), (A, C)}.


 Y = X↔Y
Y = X↔Y


