
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод ветвей и границ решения задачи коммивояжера
Формально алгоритм метода ветвей и границ выглядит следующим образом. В начале любой итерации t известна верхняя оценка На итерации 1 основной список включает две задачи: в одной из них cij изменено на ∞, а в другой – соответствующая переменная xij=1, На итерации t выполняются следующие шаги. Шаг 1. Прекратить вычисления, если основной список пуст. В противном случае выбрать одну задачу и вычеркнуть ее из основного списка. Шаг 2. Определить нижнюю оценку целевой функции для любого цикла, порождаемого выбранной задачей. Если нижняя оценка больше или равна F t (x), то принять F t+1 (x) = F t (x) и вернуться к шагу 1. В противном случае перейти к шагу 3. Шаг 3. Если текущее решение определяет цикл, то зафиксировать его, принять равным соответствующему значению целевой функции и вернуться к шагу 1. В противном случае – перейти к шагу 4. Шаг 4. Выбрать переменную хhk, не входящую в текущее решение, такую, что chk < ∞ при условии, что хhk=1 не приводит к образованию подцикла на переменных, уже вошедших в решение. При таком выборе внести в основной список две задачи. Каждую из этих задач принять идентичной задаче, выбранной на шаге 1, за исключением лишь того, что в одну из них ввести изменение chk =∞, а в другую – условие хhk =1 и
Математическая постановка транспортной задачи. В пунктах P1, P2 … Pn имеется груз в количествах a1, a2 … an. Его необходимо перевезти в пункты Q1, Q2 … Qn в количествах b1, b2, … bn. Требуется составить такой план перевозок, при котором суммарные транспортные расходы минимальны.
Обозначим через xij – количество груза перевозимого из пункта Pi в пункт Qj. cij – стоимость перевозки единицы этого груза.
Количество груза отправляемого из пункта Pi должно быть равно имеющимся запасам an.
Количество груза поставляемого в Qj должно быть равно имеющимся потребностям bn.
Целевая функция определяет стоимость перевозки всего груза.
Модифицированный распределительный метод транспортной задачи ∑ai ≠ ∑bj
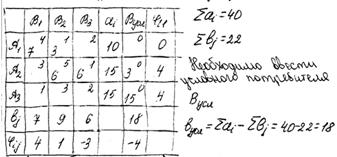
Транспортные задачи, у которых возможности и потребности не совпадают называются открытыми. Для их решения, в случае если ∑ai > ∑bj, вводят условного потребителя, для которого ci,усл =0. Если ∑ai < ∑bj, то вводят условного поставщика, для которого cусл,j=0. Таблица в таком случае будет иметь вид:
Дальнейшие вычисления происходят по алгоритму из 8 вопроса.
Распределительный метод.
1) Поиск исходного решения Первоначальное решение ищут методом северо-западного угла. Запись таблицы идет последовательно с левой верхней в правую нижнюю А1B1->АnBn
2) Проанализируем пустые(=0) клетки Исследуем перспективность клетки А1В3 полагая, что Х13=1.Для оценки переспективности пустой клетки строится прямоугольник принятия решиений, в котором все углы кроме исследуемого должны быть заняты т.у в них величины Хij<>0 После анализа всех пустых клеток выбирается клетка с максимальным значением потенциала «-», если клеток с «-» значением нет, то полученно оптимальное решение 3) Перераспределение полученного решения
Перераспределение производится в пределах многоугольника принятия решений для переспективных клеток. В клетках с «-» индексом из значений переменных вычитается минимальное значения переменной, стоящих в этих клетках и это же значение прибавляется к значению переменных, стоящих в клетках с «+» индексами. После перераспределения делается очередная итерация заключающаяся в поиске перспективной клетки и очередном перераспределении.
Цикломатическое число графа
Базисная система циклов графа – это множество линейно-независимых по модулю два циклов, такое, что любой цикл графа выражается как линейная комбинация по модулю 2 через его элементы. Цикломатическая матрица:
Цикломатическим числом графа ν(G) – называется число базисных циклов, через которые можно выразить любой другой цикл. ν(G)=m-n+1, где m – сигнатура; n – множество вершин. Для приведенного выше графа ν(G)=5-4+1=2, т.е. имеется 2 независимых цикла и что можно убрать 2 ребра так, чтобы получился связанный граф без циклов.
Теорема Эйлера: число элементов базисной системы циклов графа постоянно и равно его цикломатическому числу.
(11) Деревья. Остовное дерево минимального веса Дерево - это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность - отсутствие циклов и то, что между парами вершин имеется только по одному пути. Ориентированное (направленное) дерево - ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями Теорема. В связном графе (M, N, T) найдется частичный связный граф (M, N, T) В котором |M| - 1= |N'| = k и можно перенумеровать вершины из M числами от О до k, a дуги из N' числами от l до k таким образом, что для любой дуги u? N' выполн.
(12) Топологическая сортировка графа. Алгоритм Демукрона Топологическая сортировка - один из основных алгоритмов на графах, который примен. для реш. множества более сложных задач. Задача тополог. сортировки графа сост. в следующем: указать такой линейный порядок на его вершинах, чтобы любое ребро вело от вершины с меньшим номером к вершине с большим номером. Очевидно, что если в графе есть циклы, то такого порядка не существует. Ориентир. сетью назыв. бесконтурный ориентир. граф. В задачах подобного плана рассматриваются только конечные сети. Алгоритм Демукрона — алгоритм решения задачи тополог. сортировки, то есть упорядочения вершин графа по их уровням для бесконтурного ориентир. графа. Уровни вершин графа можно рассматривать как длины max путей от входов до этих вершин. Основная идея алгоритма Демукрона состоит в послед. удалении из сети, начиная со входов, вершин и исходящих из них дуг. Алгоритм исп. матрицу смежности вершин В типа n x n в качестве средства представления сети и основан непосредственно на определении уровня вершины и свойствах матрицы В.
Операции над графами. 1) Дополнение графа G = (x, U).
Это граф
2) Объединение графов При условии, что G = (x, U) у которого множество вершин
3) Сумма графов
Граф G = (x, U) образован путем объединения графов
4) Удаление вершины x из графа G = (x, U)
5) Удаление ребра из графа
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.158.47 (0.02 с.) |
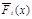 оптимального значения целевой функции. Имеется список задач (маршрутов), в котором некоторое подмножество значений cij изменено и принято равным ∞, а также подмножество { xij }={ xij | xij =1}.
оптимального значения целевой функции. Имеется список задач (маршрутов), в котором некоторое подмножество значений cij изменено и принято равным ∞, а также подмножество { xij }={ xij | xij =1}.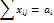
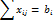
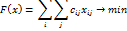







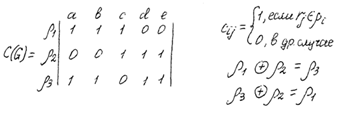
 Задача о кратчайшем остовном дереве. Пусть каждой дуге J графа (M, N, T) сопоставлено неотрицательное число l[j] именуемое длиной этой дуги Требуется построить такое остовное дерево (M, N, T) У которого сумма Длин дуг
Задача о кратчайшем остовном дереве. Пусть каждой дуге J графа (M, N, T) сопоставлено неотрицательное число l[j] именуемое длиной этой дуги Требуется построить такое остовное дерево (M, N, T) У которого сумма Длин дуг 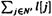 была бы минимальна.
была бы минимальна.
 , у которого носитель совпадает с исходным графом и множество дуг
, у которого носитель совпадает с исходным графом и множество дуг  есть дополнение для множества дуг U.
есть дополнение для множества дуг U. 





 не пересекаются
не пересекаются 
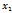 объединены с
объединены с  и дуги
и дуги  .
.

 и построения полного двудольного графа, у которого одна доля представляет собой множество
и построения полного двудольного графа, у которого одна доля представляет собой множество 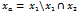 , а 2 доля
, а 2 доля 






