
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равносильные формулы. Формулы алг логики
Приведем определение формулы алгебры логики. 1) каждая «элементарная» булева функция – формула; 2) если некоторое выражение N есть формула, то 3) если некоторые выражения M и N есть формулы, то выражения 4) других формул, кроме построенных по п.п.1), 2), 3), нет. Две формулы N и M называются равносильными, если они определяют одну и ту же булеву функцию (запись N = M будет означать, что формулы N и M равносильны) Очевидно, что отношение равносильности формул алгебры логики является: 1) рефлексивным, т.е. N = N для любой формулы N; 2) симметричным, т.е. если N = M, то M = N для любых формул N и M; 3) транзитивным, т.е. если N = M и M = J, то N = J для любых формул N,M,J. Законы алгебры логики 1) 2) Назовем формулу алгебры логики
Множество булевых функций, рассматриваемое вместе с операциями отрицания, конъюнкции и дизъюнкции, называют булевой алгеброй. Теорема 1 Если формулы алгебры логики N и M равносильны, то и двойственные им формулы N* и M* равносильны. НОРМАЛЬНЫЕ ФОРМЫ Пусть G – параметр, равный 0 или 1. Введем обозначение:
Проверкой легко установить, что x G = 1, тогда и только тогда, когда Теорема 1 Всякая булева функция f(x1,x2,…,xn) может быть представлена в следующей форме:
где 1 ≤ k ≤ n, в дизъюнкции берется по всем наборам значений переменных. Разложением функции по всем переменным называется совершенной дизъюнктивной нормальной формой (сокращенная запись СДНФ) функции. Для того что бы построить СДНФ необходимо: Для каждой такой строки образуем конъюнкцию и затем все полученные конъюнкции соединяем знаком дизъюнкции. Формула вида Теорема 3 Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма.
Форма вида Теорема 4 Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма. Формула алгебры логики называется тождественно истинной, если она при всех значениях входящих в нее переменных принимает значение истинно. Формула алгебры логики называется выполнимой, если она при некоторых значениях, входящих в нее переменных, принимает значение истинно. Теорема 4 Формула алгебры логики тогда и только тогда является тождественно истинной, когда каждая дизъюнкция в ее конъюнктивной нормальной форме содержит некоторую переменную вместе с ее отрицанием. Теорема 5 Формула алгебры логики тогда и только тогда является тождественно ложной, когда каждая конъюнкция в ее дизъюнктивной форме содержит некоторую переменную вместе с ее отрицанием.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.204 (0.007 с.) |
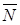 тоже формула;
тоже формула;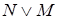 ,
, 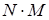 ,
, 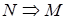 ,
, 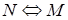 тоже формулы;
тоже формулы;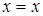 – закон тождества;
– закон тождества;  – закон противоречия;
– закон противоречия;  – закон исключительного третьего;
– закон исключительного третьего; 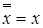 – закон двойного отрицания;
– закон двойного отрицания; 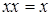 ,
, 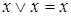 – законы идемпотентности;
– законы идемпотентности; 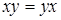 ,
, 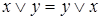 – законы коммутативности;
– законы коммутативности; 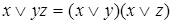 ,
, 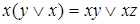 – законы дистрибутивности;
– законы дистрибутивности; 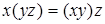 ,
, 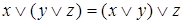 – законы ассоциативности;
– законы ассоциативности;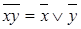 ,
,  – законы де Моргана;
– законы де Моргана;  ,
, 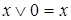 ,
, 
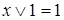 ,
, 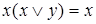 ,
, 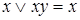 – законы поглощения;
– законы поглощения; 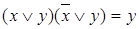 ,
, 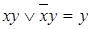 – законы склеивания.
– законы склеивания.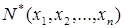 двойственной к формуле
двойственной к формуле  , если
, если 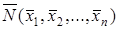 .
.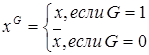
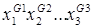 равна 1 (здесь G равен 0 или 1) тогда и только тогда, когда
равна 1 (здесь G равен 0 или 1) тогда и только тогда, когда 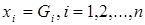 . Например, конъюнкция
. Например, конъюнкция 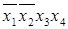 (в которой G2 = G1 = 0, G3 = G4 = 1) равна 1 только в случае, когда x 1 = x 2 = 0, x 3 = x 4 = 1.
(в которой G2 = G1 = 0, G3 = G4 = 1) равна 1 только в случае, когда x 1 = x 2 = 0, x 3 = x 4 = 1.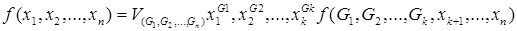 , (3.1)
, (3.1)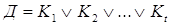 (краткая запись
(краткая запись 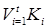 ), где
), где 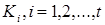 – конъюнкции
– конъюнкции 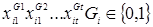 называется дизъюнктивной нормальной формой (ДНФ).
называется дизъюнктивной нормальной формой (ДНФ). (краткая запись
(краткая запись 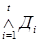 ), где
), где 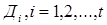 - дизъюнкции
- дизъюнкции 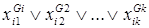 называется конъюнктивной нормальной формой (КНФ).
называется конъюнктивной нормальной формой (КНФ).


