
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения пограничного слояСтр 1 из 6Следующая ⇒
ПОГРАНИЧНЫЙ СЛОЙ. АЭРОДИНАМИЧЕСКИЙ НАГРЕВ Сопротивление удобообтекаемых тел при их движении в жидкостях или газах является в значительной степени сопротивлением от трения среды о поверхность тела. Поэтому весьма важно знать законы трения в жидкостях и газах и уметь рассчитывать сопротивление трения. Установлено, что силы трения жидкости проявляются не во всей среде, а лишь в слое, прилегающем к поверхности движущегося тела, где скорость течения резко изменяется по нормали к поверхности.
Уравнения Навье–Стокса
Запишем уравнение движения (3.8) с учетом внутреннего трения в следующем виде:
Напомним, что Составляющие тензора напряжений можно выразить с помощью обобщенного закона Ньютона (3.12):
где
Тогда, например:
С учетом выражений (3.10) для
Уравнения (7.2) и есть уравнения Навье–Стокса. В общем случае коэффициент вязкости
где Точное решение задачи обтекания какого-либо тела, сводящееся к интегрированию сложных дифференциальных уравнений при заданных граничных условиях, представляет огромные трудности. Для получения каких-либо частных решений прибегают к упрощению дифференциальных уравнений. Так Д. Стокс, решая задачу об обтекании шара потоком вязкой жидкости и сделав допущение о малости инерционных членов, отбросил их полностью. Однако такое упрощение справедливо только при очень малых числах Рейнольдса, незначительно отличающихся от единицы. О. Рейнольдс принял модель несжимаемой жидкости, отбросив полностью инерционные члены, а из вязких членов оставил главнейшие. Этот метод применяется при решении гидродинамических задач теории смазки (при малых числах При изучении обтекания тел при больших числах Рейнольдса, характерных для авиационной и ракетной техники, применяют метод упрощения уравнений Навье–Стокса, основанный на понятии пограничного слоя.
Толщина пограничного слоя
Течение жидкости в пограничном слое может быть ламинарным или турбулентным. При ламинарном течении наблюдается упорядоченное движение жидкости параллельными слоями (слоистое течение) без их перемешивания. Турбулентное течение сопровождается беспорядочным движением частиц (не молекул) жидкости, приводящим к поперечному перемешиванию вязкой среды и к пульсации параметров течения.
Формула Ньютона для силы внутреннего трения при ламинарном течении Во внешнем потоке вне пограничного слоя скорость при удалении от поверхности тела изменяется чрезвычайно медленно. Влияние вязкости здесь пренебрежимо мало, и, следовательно, можно считать, что движение подчиняется законам течения идеальной невязкой жидкости. Изучать движение среды в этой области можно с помощью уравнений Эйлера. Для исследования движения жидкости в областях с большими градиентами скорости необходимо использовать уравнения Навье–Стокса. Благодаря малой толщине пограничного слоя дифференциальные уравнения движения вязкой жидкости значительно упрощаются. При удалении от поверхности тела скорость течения увеличивается и асимптотически приближается к Обычно за толщину пограничного слоя
Толщина пограничного слоя зависит от положения точки на поверхности тела. На острой передней кромке
Толщина вытеснения
Рассмотрим секундные расходы жидкости через сечение пограничного слоя высотой
Первое слагаемое уравнения представляет собой расход невязкого газа ( Учитывая, что за пределами пограничного слоя отношение скоростей
 Если предположить, что Если предположить, что  , то рассматриваемый интеграл можно представить через площадь под кривой профиля скорости , то рассматриваемый интеграл можно представить через площадь под кривой профиля скорости  . Приведем ее к площади равновеликого прямоугольника . Приведем ее к площади равновеликого прямоугольника  (рис. 7.2). Заштрихованные площади на рис. 7.2 равны. Тогда получаем, что уменьшение расхода в пределах пограничного слоя равно (рис. 7.2). Заштрихованные площади на рис. 7.2 равны. Тогда получаем, что уменьшение расхода в пределах пограничного слоя равно  , и для несжимаемой среды , и для несжимаемой среды 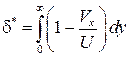 . .
Величина
Кроме того, толщина вытеснения характеризует искривление линий тока вследствие торможения потока в пограничном слое (рис. 7.3). Линии тока при обтекании пластинки невязким потоком параллельны поверхности (линия тока 1, рис. 7.3). В вязком потоке линия тока отклоняется от поверхности (линия тока 2, рис. 7.3).

Так как перед пластинкой линии тока 1 и 2 совпадают, то через сечение АВ с равномерным распределением скорости и через сечение АС с неравномерным распределением скорости протекает одинаковое количество газа (свойство трубки тока):
Отсюда
Следовательно, толщина вытеснения При решении задач с учетом влияния пограничного слоя на внешний поток можно использовать метод последовательных приближений, суть которого заключается в следующем: сначала считая газ невязким, рассчитывается распределение скоростей
Толщина потери импульса
Вследствие торможения потока в пограничном слое происходит не только уменьшение расхода по сравнению с невязким газом, но и уменьшение количества движения, проносимого жидкостью через сечение пограничного слоя, равное Толщина потери импульса
Отсюда Из сопоставления выражений для
В несжимаемой жидкости
Для области тонкого пограничного слоя, в котором собственно и проявляются силы трения, Л. Прандтль предложил особый метод упрощения уравнений движения (7.3), основанный на сравнении порядка величины членов уравнения и отбрасывания членов высшего порядка малости.
и уравнение неразрывности
Эта система уравнений полностью описывает движение вязкой жидкости в пределах пограничного слоя в рамках настоящей задачи. Оценим порядок входящих в эти уравнения членов, имея в виду, что Тогда приращение скорости
С учетом уравнения неразрывности (7.4б)
Сравнение показывает, что оба слагаемых левой части уравнения (инерционные члены) имеют один и тот же порядок малости
Внутри пограничного слоя силы вязкости и силы инерции имеют одинаковый порядок, т. е. их отношение должно быть равным единице. Тогда из уравнения (7.5), записав инерционный и вязкий члены через их порядки, получаем, что их отношение равно Проведя подобный анализ членов второго уравнения (7.4а), приходим к аналогичной выражению (7.5) упрощенной записи:
Инерционные члены этого уравнения имеют порядок
Это один из главных выводов, полученных в результате упрощения исходной системы уравнений. Таким образом, распределение давления вдоль поверхности тела совпадает с распределением давления на внешней границе пограничного слоя, которое можно найти, решая задачу обтекания данного тела невязким (потенциальным) потоком.
Так как
Система уравнений (7.6) интегрируется при следующих граничных условиях: 1) при 2) при
В сжимаемом газе
Для установившегося плоскопараллельного потока сжимаемого газа в уравнениях Навье–Стокса (7.2) произведем оценку порядка величин членов этих уравнений для пограничного слоя несжимаемой жидкости. Тогда первое уравнение системы
после анализа порядков величин его членов упрощается и запишется следующим образом:
Вторым уравнением системы (7.2) так же, как и для несжимаемой жидкости, можно пренебречь. Из него также следует, что Уравнение неразрывности для установившегося движения сжимаемой жидкости (3.1а) для плоского случая запишем как
Так как в уравнении (7.7) коэффициент вязкости
где Таким образом, для установившегося движения сжимаемого газа в пограничном слое необходимо решать систему трех уравнений (7.7). Основные неизвестные в этой системе уравнений – Решение дифференциальных уравнений пограничного слоя, как для сжимаемой, так и для несжимаемой жидкости, достаточно сложная процедура даже для простейших тел. В связи с этим используют приближенные методы решения задач пограничного слоя, основанные на рассмотрении интегрального соотношения, являющегося математическим выражением теоремы об изменении количества движения. В несжимаемой среде
Решение задачи об обтекании плоской пластинки в теории сопротивления играет большую роль. Найденная для пластинки зависимость
Для плоской пластинки (рис. 7.6) скорость потенциального течения
Для решения задачи о пограничном слое введем дополнительно еще два соотношения: 1) закон распределения скорости по толщине пограничного слоя 2) уравнение, связывающее касательное напряжение на стенке Вид этих соотношений зависит от состояния пограничного слоя.
Ламинарный пограничный слой
Рассмотрим закон распределения скорости в виде полинома третьей степени (метод Польгаузена)
Коэффициенты полинома Кинематические граничные условия: 1) при 2) при Динамические граничные условия: 1) при 2) при Подставляя указанные граничные условия в уравнения (7.11), получим следующую систему уравнений для определения коэффициентов
В результате ее решения определим значения коэффициентов:
Выражение для
Вычислим интегралы, входящие в интегральное соотношение:
и
Подставив эти интегралы в интегральное соотношение (7.10), получим обыкновенное дифференциальное уравнение:
Группируя подобные члены и разделяя переменные, получаем В итоге, после небольших преобразований получаем формулу для расчета толщины пограничного слоя:
Как следует из уравнения (7.13), толщина ламинарного пограничного слоя нарастает по параболическому закону. Тогда толщина вытеснения и толщина потери импульса для ламинарного пограничного слоя будут следующие: Введем в рассмотрение местный коэффициент трения
Подставив выражение (7.12) в выражение (7.14) с учетом уравнения (7.13), получаем следующее:
Формула (7.15) показывает, что местный коэффициент трения, имея максимум вблизи передней кромки, уменьшается при удалении от нее. Найдем силу трения, действующую на пластинку, учитывая тот факт, что пограничный слой есть на обеих сторонах пластинки (см. рис. 7.6). Запишем выражения для
и через касательные напряжения (или местный коэффициент трения):
Приравняв правые части этих выражений, получим зависимость для расчета коэффициента сопротивления трения плоской пластинки через местный коэффициент трения:
С учетом формулы (7.15) формула для коэффициента сопротивления трения плоской пластинки при ламинарном пограничном слое принимает вид
В уравнении (7.17) в качестве характерного линейного размера в числе Рейнольдса используется хорда пластинки В сжимаемом газе
Рассмотрим некоторые особенности пограничного слоя в сжимаемом газе. При малых скоростях движения кинетический нагрев газа вследствие его торможения в пограничном слое на поверхности ЛА практически отсутствует, так как температура торможения очень мало отличается от температуры потока. Например, при числе Маха Нам уже известно, что по сечению пограничного слоя
Формула для расчета температуры восстановления получается из формулы для расчета
где
Среднее значение числа Прандтля для воздуха равно Тогда для воздуха (
Учитывая, что значительное повышение температуры наблюдается только в тонком слое вблизи стенки, вводится понятие о тепловом (температурном) пограничном слое, в пределах которого температура изменяется от температуры газа вблизи стенки Изменение температуры в пограничном слое приводит к изменению плотности газа
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.143.31 (0.177 с.) |
 В отличие от идеальной жидкости, которая при своем движении скользит по обтекаемой поверхности, реальная вязкая жидкость полностью затормаживается на ней. Частицы, прилегающие к поверхности обтекаемого тела, сцепляясь с ней, тормозят вышележащие слои жидкости. Вследствие этого вблизи поверхности скорость жидкости изменяется от
В отличие от идеальной жидкости, которая при своем движении скользит по обтекаемой поверхности, реальная вязкая жидкость полностью затормаживается на ней. Частицы, прилегающие к поверхности обтекаемого тела, сцепляясь с ней, тормозят вышележащие слои жидкости. Вследствие этого вблизи поверхности скорость жидкости изменяется от  на стенке до скорости набегающего потока
на стенке до скорости набегающего потока  или скорости потенциального течения
или скорости потенциального течения  на некотором расстоянии от нее. Даже при движении жидкостей, вязкость которых незначительна (вода, воздух), подобное нарастание скорости совершается достаточно быстро. В результате, у поверхности тела, обтекаемого маловязкой жидкостью, есть очень тонкий слой, называемый пограничным слоем. Пограничный слой (рис. 7.1) представляет собой область больших значений градиентов скорости по нормали к поверхности. Внутри пограничного слоя сила вязкостного трения имеет такой же порядок, как и все остальные силы, учитываемые в уравнениях движения.
на некотором расстоянии от нее. Даже при движении жидкостей, вязкость которых незначительна (вода, воздух), подобное нарастание скорости совершается достаточно быстро. В результате, у поверхности тела, обтекаемого маловязкой жидкостью, есть очень тонкий слой, называемый пограничным слоем. Пограничный слой (рис. 7.1) представляет собой область больших значений градиентов скорости по нормали к поверхности. Внутри пограничного слоя сила вязкостного трения имеет такой же порядок, как и все остальные силы, учитываемые в уравнениях движения.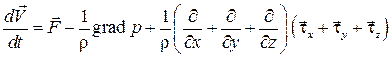 . (7.1)
. (7.1) представляют собой касательные напряжения от силы трения, действующие на площадки, перпендикулярные соответствующим осям координат. Каждая из этих составляющих, в свою очередь, может быть представлена в виде суммы трех проекций на оси координат. Таким образом, мы имеем тензор напряжений (3.10), симметричный относительно главной диагонали, т. е.
представляют собой касательные напряжения от силы трения, действующие на площадки, перпендикулярные соответствующим осям координат. Каждая из этих составляющих, в свою очередь, может быть представлена в виде суммы трех проекций на оси координат. Таким образом, мы имеем тензор напряжений (3.10), симметричный относительно главной диагонали, т. е.  ,
, 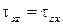 ,
,  .
.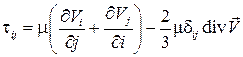 ,
, имеет вид телеграфного сигнала (или единичной матрицы), принимая значения
имеет вид телеграфного сигнала (или единичной матрицы), принимая значения 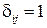 при
при  или
или  при
при  ;
;  и
и  – координатные направления.
– координатные направления. ,
,  .
. ,…, расписав каждую из составляющих
,…, расписав каждую из составляющих  тензора напряжений, запишем уравнение движения (7.1) в проекциях на оси координат:
тензора напряжений, запишем уравнение движения (7.1) в проекциях на оси координат: (7.2)
(7.2) зависит от температуры. Если считать
зависит от температуры. Если считать  , то уравнения Навье–Стокса будут иметь вид
, то уравнения Навье–Стокса будут иметь вид ,
, , (7.3)
, (7.3)
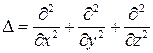 – оператор Лапласа.
– оператор Лапласа. ). Другие авторы вместе с вязкими членами оставили в уравнении только важнейшие из инерционных членов, которые к тому же линеаризируются путем замены неизвестной скорости перед производной ее характерным значением. Однако и этот метод применим при небольших числах
). Другие авторы вместе с вязкими членами оставили в уравнении только важнейшие из инерционных членов, которые к тому же линеаризируются путем замены неизвестной скорости перед производной ее характерным значением. Однако и этот метод применим при небольших числах  показывает, что внутри пограничного слоя и в следе за телом, где градиенты скорости значительны, силой внутреннего трения пренебрегать нельзя, и среду, движущуюся внутри этих областей, следует считать вязкой даже при малых значениях коэффициента вязкости.
показывает, что внутри пограничного слоя и в следе за телом, где градиенты скорости значительны, силой внутреннего трения пренебрегать нельзя, и среду, движущуюся внутри этих областей, следует считать вязкой даже при малых значениях коэффициента вязкости. поэтому толщина пограничного слоя величина достаточно условная.
поэтому толщина пограничного слоя величина достаточно условная. в данной точке поверхности принимают расстояние от тела до такой точки, в которой действительная скорость потока
в данной точке поверхности принимают расстояние от тела до такой точки, в которой действительная скорость потока  .
. и растет с удалением от передней кромки.
и растет с удалением от передней кромки. .
. – плотность невязкого газа,
– плотность невязкого газа,  – плотность вязкого газа, которая зависит от скорости течения и, следовательно, переменна по толщине пограничного слоя).
– плотность вязкого газа, которая зависит от скорости течения и, следовательно, переменна по толщине пограничного слоя).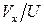 изменяется очень мало (
изменяется очень мало (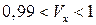 ), интеграл в выражении для разности расходов в пределах от 0 до
), интеграл в выражении для разности расходов в пределах от 0 до  , называемая толщиной вытеснения, – условная толщина некоторого слоя, сквозь сечение которого в единицу времени и при постоянной во всех сечениях скорости
, называемая толщиной вытеснения, – условная толщина некоторого слоя, сквозь сечение которого в единицу времени и при постоянной во всех сечениях скорости  Толщина вытеснения характеризует уменьшение секундного расхода газа через сечение пограничного слоя вследствие торможения потока в пограничном слое.
Толщина вытеснения характеризует уменьшение секундного расхода газа через сечение пограничного слоя вследствие торможения потока в пограничном слое.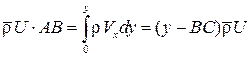 .
. . В данном случае
. В данном случае  – смещение линии тока вязкого потока по отношению к линии тока невязкого потока. В сечении, где
– смещение линии тока вязкого потока по отношению к линии тока невязкого потока. В сечении, где  (а в точке
(а в точке  линия тока 2 пересекает границу пограничного слоя), получаем
линия тока 2 пересекает границу пограничного слоя), получаем .
. , и в пределах толщины пограничного слоя
, и в пределах толщины пограничного слоя  имеет тот же порядок что и
имеет тот же порядок что и  и давлений
и давлений  по поверхности тела; затем на основании полученных данных рассчитывается толщина пограничного слоя и толщина вытеснения; производится изменение (утолщение) контура поверхности на
по поверхности тела; затем на основании полученных данных рассчитывается толщина пограничного слоя и толщина вытеснения; производится изменение (утолщение) контура поверхности на  .
. – условная толщина некоторого слоя, сквозь сечение которого в единицу времени с постоянной скоростью
– условная толщина некоторого слоя, сквозь сечение которого в единицу времени с постоянной скоростью  .
.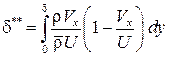 – для сжимаемой жидкости, и
– для сжимаемой жидкости, и  – для несжимаемой жидкости.
– для несжимаемой жидкости.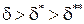 .
. Пусть поток движется вдоль твердой прямолинейной границы в направлении оси ОХ (рис. 7.4). Вдоль этой границы образуется пограничный слой, толщина которого
Пусть поток движется вдоль твердой прямолинейной границы в направлении оси ОХ (рис. 7.4). Вдоль этой границы образуется пограничный слой, толщина которого  , скорость течения не зависит от времени, плотность постоянная). Массовыми силами для газа можно пренебречь (
, скорость течения не зависит от времени, плотность постоянная). Массовыми силами для газа можно пренебречь (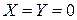 ). С учетом принятых допущений запишем уравнения Навье–Стокса следующим образом:
). С учетом принятых допущений запишем уравнения Навье–Стокса следующим образом: , (7.4)
, (7.4)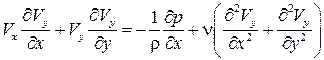 , (7.4а)
, (7.4а) в виде
в виде . (7.4б)
. (7.4б)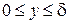 , т. е.
, т. е.  имеет порядок толщины пограничного слоя
имеет порядок толщины пограничного слоя 
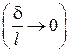 . Скорость в пределах пограничного слоя
. Скорость в пределах пограничного слоя  (
( ), продольная координата
), продольная координата  , т. е.
, т. е.  ~
~ 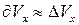 имеет порядок величины скорости во внешнем потоке
имеет порядок величины скорости во внешнем потоке  ~
~ 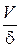 ;
;  ~
~ 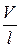 ;
; 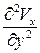 ~
~ 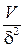 ;
;  ~
~  .
.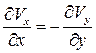 ~
~  , то
, то 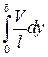 ~
~ 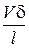 ,
,  ~
~  ,
,  ~
~  . Записав порядки величин членов уравнения (7.4), сравним их:
. Записав порядки величин членов уравнения (7.4), сравним их: .
. . Вязкие члены (в скобках правой части) имеют разный порядок, причем первое слагаемое существенно меньше второго: отношение первого ко второму равно
. Вязкие члены (в скобках правой части) имеют разный порядок, причем первое слагаемое существенно меньше второго: отношение первого ко второму равно  . Поэтому первым слагаемым можно пренебречь, и уравнение (7.4) запишется в несколько упрощенном виде:
. Поэтому первым слагаемым можно пренебречь, и уравнение (7.4) запишется в несколько упрощенном виде: . (7.5)
. (7.5) и отсюда
и отсюда  откуда получается вполне очевидное соотношение:
откуда получается вполне очевидное соотношение:  ~
~  .
.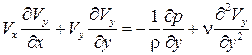 .
. и относятся к инерционным членам первого уравнения как
и относятся к инерционным членам первого уравнения как  . Поэтому инерционными и вязкими членами второго уравнения можно пренебречь и в задаче исследования течения в пограничном слое вообще не учитывать. Тогда из второго уравнения системы с достаточной точностью можно записать следующее:
. Поэтому инерционными и вязкими членами второго уравнения можно пренебречь и в задаче исследования течения в пограничном слое вообще не учитывать. Тогда из второго уравнения системы с достаточной точностью можно записать следующее: .
. То есть, давление внутри пограничного слоя не меняется вдоль нормали к контуру тела и равняется давлению на внешней границе пограничного слоя.
То есть, давление внутри пограничного слоя не меняется вдоль нормали к контуру тела и равняется давлению на внешней границе пограничного слоя.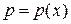 и
и  =
= 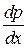 . В результате упрощений получаем систему уравнений, описывающих движение вязкой жидкости в пределах пограничного слоя:
. В результате упрощений получаем систему уравнений, описывающих движение вязкой жидкости в пределах пограничного слоя: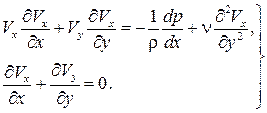 (7.6)
(7.6)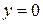 – на внутренней границе пограничного слоя (на стенке)
– на внутренней границе пограничного слоя (на стенке)  ;
;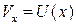 .
.

 . (7.7)
. (7.7) . (7.7а)
. (7.7а)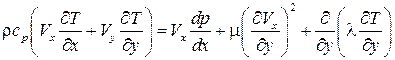 , (7.7б)
, (7.7б) – коэффициент теплопроводности
– коэффициент теплопроводности  .
. . Так как
. Так как  можно считать известным. С помощью уравнения состояния плотность определится как
можно считать известным. С помощью уравнения состояния плотность определится как  , а коэффициенты вязкости
, а коэффициенты вязкости  и величина коэффициента сопротивления трения могут быть использованы при приближенных расчетах других удобообтекаемых тел.
и величина коэффициента сопротивления трения могут быть использованы при приближенных расчетах других удобообтекаемых тел. Задача расчета пограничного слоя в несжимаемой среде сводится к определению закона изменения толщины пограничного слоя, т. е.
Задача расчета пограничного слоя в несжимаемой среде сводится к определению закона изменения толщины пограничного слоя, т. е. 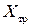 при условии, что известны скорость
при условии, что известны скорость  .
. , градиент давления вдоль пластинки
, градиент давления вдоль пластинки  (пластинка – тело с нулевым градиентом давления вдоль ее хорды). С учетом вышеизложенного интегральное соотношение (7.8) приобретает вид
(пластинка – тело с нулевым градиентом давления вдоль ее хорды). С учетом вышеизложенного интегральное соотношение (7.8) приобретает вид . (7.10)
. (7.10)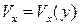 ;
; с толщиной пограничного слоя
с толщиной пограничного слоя  . (7.11)
. (7.11) определим из граничных кинематических и динамических условий:
определим из граничных кинематических и динамических условий: ;
; .
. и из первого уравнения системы (7.6) для пограничного слоя получаем
и из первого уравнения системы (7.6) для пограничного слоя получаем  , но
, но  и тогда
и тогда  ;
; обращаются в нуль, и отсюда
обращаются в нуль, и отсюда  .
. ,
, 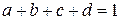 ,
, 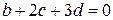 ,
, 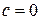 .
.

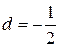 . Следовательно, закон распределения скорости по сечению ламинарного пограничного слоя принимает вид
. Следовательно, закон распределения скорости по сечению ламинарного пограничного слоя принимает вид . (7.11а)
. (7.11а) . Из уравнения (7.11а) производная
. Из уравнения (7.11а) производная  , отсюда:
, отсюда: . (7.12)
. (7.12)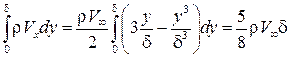

 .
.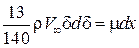 . После интегрирования имеем следующее:
. После интегрирования имеем следующее:  . Значение произвольной постоянной
. Значение произвольной постоянной  толщина пограничного слоя
толщина пограничного слоя  .
. , или
, или  . (7.13)
. (7.13) и
и  .
. , представляющий собой отношение касательных напряжений к скоростному напору:
, представляющий собой отношение касательных напряжений к скоростному напору: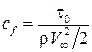 . (7.14)
. (7.14) или
или 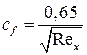 . (7.15)
. (7.15)
 .
. . (7.16)
. (7.16)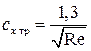 . (7.17)
. (7.17) .
. . Поэтому при отсутствии подвода или отвода тепла через поверхность тела температура газа по толщине пограничного слоя может быть принята постоянной и равной температуре среды на внешней границе пограничного слоя или
. Поэтому при отсутствии подвода или отвода тепла через поверхность тела температура газа по толщине пограничного слоя может быть принята постоянной и равной температуре среды на внешней границе пограничного слоя или  (для плоской пластинки).
(для плоской пластинки). ). Таким образом, при расчете пограничного слоя, образующегося на поверхности тела при малых скоростях движения, можно считать параметры течения
). Таким образом, при расчете пограничного слоя, образующегося на поверхности тела при малых скоростях движения, можно считать параметры течения  в пограничном слое постоянными.
в пограничном слое постоянными. При больших скоростях движения кинетический разогрев газа значительно сильнее, и в пограничном слое происходит существенное повышение температуры. Для теплоизолированного пограничного слоя (тепло не отводится через поверхность тела, не излучается с его поверхности в пространство) температура газа у стенки несколько меньше температуры торможения
При больших скоростях движения кинетический разогрев газа значительно сильнее, и в пограничном слое происходит существенное повышение температуры. Для теплоизолированного пограничного слоя (тепло не отводится через поверхность тела, не излучается с его поверхности в пространство) температура газа у стенки несколько меньше температуры торможения  , так как часть тепловой энергии уносится самими молекулами при их хаотическом движении. Температура газа у теплоизолированной стенки равна температуре восстановления
, так как часть тепловой энергии уносится самими молекулами при их хаотическом движении. Температура газа у теплоизолированной стенки равна температуре восстановления  (рис. 7.9).
(рис. 7.9). :
: , (7.21)
, (7.21) и состояния пограничного слоя.
и состояния пограничного слоя. Число
Число  представляет собой отношение количества тепла, выделяемого вследствие трения, к количеству тепла, уносимого молекулами при их непрерывном перемешивании.
представляет собой отношение количества тепла, выделяемого вследствие трения, к количеству тепла, уносимого молекулами при их непрерывном перемешивании.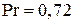 . В зависимости от состояния пограничного слоя коэффициент восстановления температуры равен
. В зависимости от состояния пограничного слоя коэффициент восстановления температуры равен  – для ламинарного пограничного слоя и
– для ламинарного пограничного слоя и 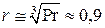 – для турбулентного.
– для турбулентного.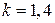 ) формула (7.21) для расчета температуры восстановления принимает следующий вид:
) формула (7.21) для расчета температуры восстановления принимает следующий вид: – для ламинарного пограничного слоя;
– для ламинарного пограничного слоя; – для турбулентного слоя.
– для турбулентного слоя. до температуры
до температуры 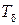 на внешней границе слоя. В общем случае толщина теплового пограничного слоя не совпадает с толщиной динамического (скоростного) пограничного слоя.
на внешней границе слоя. В общем случае толщина теплового пограничного слоя не совпадает с толщиной динамического (скоростного) пограничного слоя. из-за разогрева газа, плотность его у стенки значительно меньше, чем во внешнем потоке. При нагреве существенно изменяются коэффициенты вязкости
из-за разогрева газа, плотность его у стенки значительно меньше, чем во внешнем потоке. При нагреве существенно изменяются коэффициенты вязкости  , а также коэффициент теплопроводности
, а также коэффициент теплопроводности 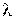 .
.


