
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прикладные задачи линейного программирования в транспортных системах.
Задача №1. Определение оптимальной структуры флота судоходной компании. Постановка задачи. Судоходная компания (СК) занимается перевозками грузов. В ее составе имеется В соответствии с долгосрочными договорами объемы перевозок на n направлениях возрастут, и их годовые объемы составят Определить оптимальную структуру флота СК, обеспечивающую освоение перевозок с максимальной прибылью. Под структурой флота понимается типы судов и их количество. Для решения задачи используется такой подход. Из сетки типоразмеров судов отбираются подходящие по назначению типы судов. При отборе судов также учитываются глубины в портах захода, оснащенность их перегрузочным оборудованием, гидрометеорологические условия на трассе и в портах и др. Эти суда будем называть претендентами на пополнение флота СК. Суда - претенденты могут быть отобраны и из других источников (данные о продаже судов, сдаче их в аренду и т.п.). Программу оптимизации структуры флота СК (другими словами, оптимизацию пополнения флота СК новыми судами) будем определять на основе совместной расстановки действующих судов и судов-претендентов на пополнение на перспективных направлениях. Будем считать, что число судов новых типов, которые можно купить или построить на судостроительных заводах за год, не превышает Математическая модель задачи в общем виде такова:
где
Экономический смысл математической модели (6)-(10): (6) – ЦФ отражает годовую прибыль судов всех типов на всех направлениях, которую нужно максимизировать. (7) – ограничение по обязательному освоению перевозок на всех направлениях. (8) – ограничение по обязательному использованию действующих типов судов. (9) – ограничение по количеству судов-претендентов, которые могут построить судостроительные заводы (либо ограничение по количеству судов, которые продаются или сдаются в аренду). (10) – условие неотрицательности переменных.
Число судов, подлежащих постройке (покупке) -
Задача определения оптимальной структуры флота СК должна быть поставлена как задача целочисленного программирования. Особенностью математической модели в этом случае будет являться то, что требование целочисленности должно быть наложено не на каждую переменную
Для действующих типов судов это условие будет выполняться автоматически ввиду того, что ограничения по ним задаются равенствами. Математическая модель задачи будет иметь вид:
Задача №2. Выбор вида транспорта для доставки грузов. Постановка задачи. В m пунктах отправления А1, А2, …, Аi, …, Am имеется однородный груз в количестве а1, а2, …, ai, …, am (ед.). Груз нужно доставить в n пунктов назначения В1, В2, …, Вj, …, Bn, потребности которых составляют b1, b2, …, bj, …, bn (ед.). Груз может перевозиться t видами транспорта Т1, Т2, …, Tp, …, Tt. Известна стоимость доставки единицы груза от каждого отправителя любому получателю любым видом транспорта Составить план перевозки грузов, обеспечивающий вывоз всех грузов от всех отправителей, удовлетворение потребностей всех получателей при минимальных расходах. В качестве параметров управления Математическая модель задачи имеет вид:
(17) – ЦФ отражает расходы на все перевозки, которые нужно минимизировать. (18) – ограничение по обязательному вывозу груза от всех отправителей. (19) – ограничение по удовлетворению потребностей всех получателей. (20) – условие неотрицательности переменных. В рассмотренной выше постановке задачи предполагалось, что запасы равны потребностям:
где bj – пропускная способность j-ого порта. Рассмотрим некоторые решения постановок задачи о выборе вида транспорта для доставки грузов.
Пусть заданы провозные способности разных видов транспорта. Обозначим их
В задаче могут рассматриваться перевозки разнородных грузов. Обозначим род груза текущим индексом k, Математическая модель (17)-(20) примет вид:
Полученную модель можно дополнить при необходимости ограничениями (21), внеся в них соответствующие изменения. Задача №3. Выбор маршрута доставки грузов. Рассмотрим задачу выбора маршрута доставки грузов от поставщиков к потребителям в смешанном сообщении с выбором вида транспорта. Рассматриваются перевозки в импорте. В m пунктах имеется однородный груз, который нужно доставить n получателям. Доставка груза осуществляется в смешанном сообщении (морская часть пути и наземная, где есть возможность выбора вида транспорта для доставки: железнодорожный, автомобильный). Перевалка груза может осуществляться в Необходимо выбрать маршрут доставки груза от отправителей к получателям, обеспечивающий минимальные расходы. Введем обозначения: i – порт отправления груза,
j – пункт назначения, p – вид транспорта, ai – количество груза в порту отправления i; bj – потребность в пункте назначения j;
Введем 2 группы переменных:
Математическая модель задачи имеет вид:
(26) – ЦФ отражает расходы на перевозку груза по всему пути его доставки, которые нужно минимизировать; (27) – ограничение по вывозу груза из портов отправления; (28) – ограничение по удовлетворению потребностей получателей; (29) – балансовые уравнения, смысл которых состоит в том, что груз поступивший в порт перевалки (левая часть), должен быть из него отправлен (правая часть); (30) – условие неотрицательности переменных.
|
||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.68.14 (0.022 с.) |
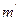 типов судов, число судов в каждом типе
типов судов, число судов в каждом типе 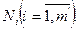 .
.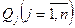 тыс. т. Имеющихся судов недостаточно для освоения перевозок.
тыс. т. Имеющихся судов недостаточно для освоения перевозок.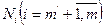 .
.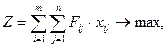 (6)
(6)
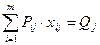
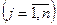 , (7)
, (7)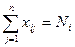
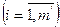 , (8)
, (8)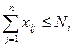
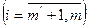 , (9)
, (9)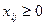
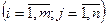 (10)
(10)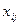 - число судов i-ого типа на j-ом направлении,
- число судов i-ого типа на j-ом направлении,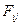 - прибыль одного судна i-ого типа на j-ом направлении, тыс. долл.,
- прибыль одного судна i-ого типа на j-ом направлении, тыс. долл.,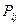 - годовая провозная способность одного судна i-ого типа на j-ом направлении, тыс. т.
- годовая провозная способность одного судна i-ого типа на j-ом направлении, тыс. т.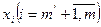 , определяется соотношением:
, определяется соотношением: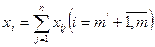 .
.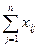 - целое
- целое 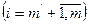 .
.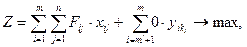 (11)
(11)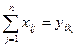
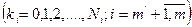 , (14)
, (14)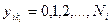
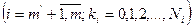 (15)
(15)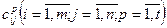 .
.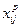 примем количество груза, которое может быть перевезено от i-ого отправителя j-ому получателю транспортом вида p.
примем количество груза, которое может быть перевезено от i-ого отправителя j-ому получателю транспортом вида p.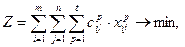 (17)
(17)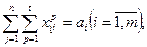 (18)
(18)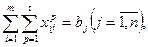 (19)
(19)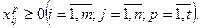 (20)
(20)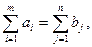 т.е. задача сбалансирована. В зависимости от постановки задачи условие баланса не всегда соблюдается. Например, если пунктами назначения являются порты перевалки, то ограничения могут иметь вид:
т.е. задача сбалансирована. В зависимости от постановки задачи условие баланса не всегда соблюдается. Например, если пунктами назначения являются порты перевалки, то ограничения могут иметь вид: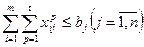 ,
,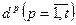 . В этом случае в математическую модель (17)-(20) нужно ввести дополнительную группу ограничений по провозной способности видов транспорта, которая будет иметь вид:
. В этом случае в математическую модель (17)-(20) нужно ввести дополнительную группу ограничений по провозной способности видов транспорта, которая будет иметь вид: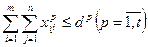 . (21)
. (21)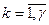 .
.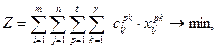 (22)
(22)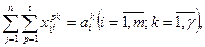 (23)
(23)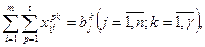 (24)
(24)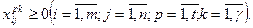 (25)
(25)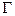 портах. Известна стоимость доставки 1 т груза из каждого иностранного порта в каждый порт перевалки (морская часть пути) и из каждого порта перевалки получателям каждым видом транспорта.
портах. Известна стоимость доставки 1 т груза из каждого иностранного порта в каждый порт перевалки (морская часть пути) и из каждого порта перевалки получателям каждым видом транспорта.
 - порт перевалки,
- порт перевалки, 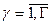 ;
; ;
;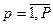 ;
;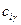 - стоимость перевозки 1 т груза от i-ого поставщика к порту перевалки
- стоимость перевозки 1 т груза от i-ого поставщика к порту перевалки  - стоимость перевозки 1 т груза от порта перевалки
- стоимость перевозки 1 т груза от порта перевалки 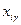 - количество груза, которое может быть перевезено из i-ого порта отправления в порт перевалки
- количество груза, которое может быть перевезено из i-ого порта отправления в порт перевалки  - количество груза, которое может быть перевезено из порта перевалки
- количество груза, которое может быть перевезено из порта перевалки 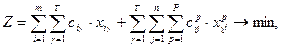 (26)
(26) , (27)
, (27) , (28)
, (28)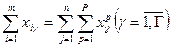 , (29)
, (29)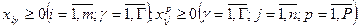 (30)
(30)


