
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класичні критерії прийняття рішень ⇐ ПредыдущаяСтр 4 из 4
Мінімаксний критерій Вальда.
Правило вибору рішення відповідно до мінимаксного критерію (ММ-критерію) можна інтерпретувати в такий спосіб:
матриця рішень доповнюється ще одним стовпцем з найменших результатів eir кожного рядка. Необхідно вибрати ті варіанти в рядках яких коштують найбільше значення eir цього стовпця. Обрані таким чином варіанти цілком виключають ризик. Це означає, що особа, що приймає рішення не може зіштовхнутися з гіршим результатом, ніж той, на який він орієнтується. Ця властивість дозволяє вважати Мм-критерій одним з фундаментальних. Застосування Мм-критерію буває виправдане, якщо ситуація, у якій приймається рішення наступна: 1. Про можливість появи зовнішніх станів Fj нічого не відомо; 2. Приходиться вважатися з появою різних зовнішніх станів Fj; 3. Рішення реалізується тільки один раз; 4. Необхідно виключити будь який ризик.
Критерій Байєса – Лапласа. Позначимо через qi – імовірність появи зовнішнього стану Fj. Відповідне правило вибору можна інтерпретувати в такий спосіб:
матриця рішень доповнюється ще одним стовпцем, що містить математичне очікування значень кожного з рядків. Вибираються ті варіанти, у рядках яких стоїть найбільше значення eir цього стовпця. При цьому вважають, що ситуація, у якій приймається рішення, характеризується наступними обставинами: 1. Імовірності появи станів Fj відомі і не залежать від часу. 2. Рішення реалізується (теоретично) нескінченно багато разів. 3. Для малої кількості реалізацій рішення допускається деякий ризик. При досить великій кількості реалізацій середнє значення поступово стабілізується. Тому при повній (нескінченної) реалізації який-небудь ризик практично виключений. Таким чином, критерій Байеса-Лапласа (BL-критерій) більш оптимістичний, ніж мінімаксний критерій Вальда, однак він припускає велику інформованість і досить тривалу реалізацію. Критерій мінімального ризику Севіджа. Введемо позначення:
Величину aij можна трактувати як максимальний додатковий виграш, що досягається, якщо в стані Fj замість варіанта Ei вибирати інший, оптимальний для цього зовнішнього стану варіант. Величину aij можна інтерпретувати і як втрати (штрафи), що виникають у стані Fj при заміні оптимального для нього варіанта на варіант Ei. В останньому випадку eir є максимально можливою (по всіх зовнішніх станах Fj, j =
Відповідне критерію Севиджа правило вибору тепер трактується так: 1) Кожен елемент матриці рішень віднімається з найбільшого результату max eij відповідного стовпця. 2. Різниці aij утворюють матрицю ризиків. Ця матриця поповнюється стовпцем найбільших різниць eir. Вибирають ті варіанти, у рядках яких стоїть найменше для цього стовпця значення. Вимоги, стосовно до ситуації, у якій приймається рішення, збігаються з вимогами до ММ-критерію.
Приклад і висновки. З вимог, що висуваються до розглянутих критеріїв стає ясно, що в наслідку їх жорстких вихідних позицій вони можуть бути застосовані тільки для ідеалізованих практичних рішень. У випадку, коли можлива занадто сильна ідеалізація, можна застосовувати одночасно по черзі різні критерії. Після цього серед декількох варіантів ОПР вольовим методом вибирає остаточне рішення. Такий підхід дозволяє, по-перше, краще проникнути в усі внутрішні зв'язки проблеми прийняття рішень і, по-друге, послабляє вплив суб'єктивного фактору. Приклад. При роботі ЕОМ необхідно періодично припиняти обробку інформації і перевіряти ЕОМ на наявність у ній вірусів. Припинення в обробці інформації приводять до визначених економічних витрат. У випадку ж якщо вірус вчасно виявлений не буде, можливі втрата і деякої частини інформації, що приведе і ще до великих збитків. Варіанти рішення такі: Е1 – повна перевірка; Е2 – мінімальна перевірка; Е3 – відмовлення від перевірки. ЕОМ може знаходитися в наступних станах: F1 – вірус відсутній; F2 – вірус є, але він не встиг зашкодити інформації; F3 – є файли, що потребують відновлення. Результати, що включають витрати на пошук вірусу і його ліквідацію, а також витрати, зв'язані з відновленням інформації мають вигляд:
Відповідно до ММ-критерію варто проводити повну перевірку. Критерій Байєса-Лапласа, у припущенні, що всі стани машини рівноімовірні P(Fj) = qj = 0.33, рекомендує відмовитися від перевірки. Матриця ризиків для цього приклада і їхня оцінка (у тисячах) відповідно до критерію Севіджа має вигляд:
Приклад спеціально підібраний так, що кожен критерій пропонує нове рішення. Невизначеність стану, у якому перевірка застає ЕОМ, приводить до невизначеності, який критерій обирати. Оскільки різні критерії зв'язані з різними умовами, у яких приймається рішення, краще усього для порівняльної оцінки рекомендації тих чи інших критеріїв одержати додаткову інформацію про саму ситуацію. Зокрема, якщо прийняте рішення відноситься до сотень машин з однаковими параметрами, то рекомендується застосовувати критерій Байеса-Лапласа. Якщо ж кількість машин не велика, краще використовувати критерії Вальда чи Севіджа.
Похідні критерії.
Критерій Гурвіца. Намагаючись зайняти найбільш врівноважену позицію, Гурвіц припустив оцінну функцію, що знаходиться десь між точкою зору крайнього оптимізму і крайнього песимізму:
де С – ваговий множник, що характеризує ступінь оптимізму. Правило вибору відповідно до критерію Гурвіца, формується в такий спосіб:
матриця рішень доповнюється стовпцем, що містить середнє зважене найменшого і найбільшого результатів для кожного рядка. Вибираються тільки ті варіанти, у рядках яких стоять найбільші елементи eir цього стовпця. При С =1 критерій Гурвіца перетворюється в критерій Вальда. При С = 0 він перетворюється на критерій “азартного гравця”
тобто ми стаємо на точку зору азартного гравця, що робить ставку на те, що йому «випаде» найвигідніший випадок. У технічних прикладах складно вибрати ваговий множник С, тому що важко знайти кількісну характеристику для тих часток оптимізму і песимізму, що присутні при прийнятті рішення. Тому найчастіше С = 0.5. Критерій Гурвіца застосовується у випадку, коли: 1) про імовірності появи станів Fj нічого не відомо; 2) с появою стану Fj необхідно рахуватися; 3) реалізується тільки мала кількість рішень; 4) допускається деякий ризик.
Критерій Ходжа–Лемана.
Цей критерій спирається одночасно на критерій Вальда і критерій Байєса-Лапласа. За допомогою параметра n виражається ступінь довіри до використовуваного розподілу імовірностей. Якщо довіра велика, то домінує критерій Баеса-Лапласа, у противному випадку – критерій Вальда, тобто ми знаходимо
Правило вибору, що відповідає критерію Ходжа-Лемана формується в такий спосіб:
матриця рішень При n = 1 критерій Ходжа-Лемана переходить у критерій Байеса-Лапласа, а при n = 0 стає мінімаксним. Вибір n є суб'єктивним тому що ступінь імовірності якої-небудь функції розподілу є справою “темною”.
Для застосування критерію Ходжа-Лемана бажано, щоб ситуація в який приймається рішення, задовольняла властивостям: 1) імовірності появи стану Fj невідомі, але деякі припущення про розподіл імовірностей можливі; 2) прийняте рішення теоретично допускає нескінченно багато реалізацій; 3) при малих кількостях реалізацій допускається деякий ризик.
Критерій Гермейєра.
Цей критерій орієнтований на величину втрат, тобто на від’ємні значення всіх eij. При цьому
Так як у практичних задачах переважно мають справу з цінами і витратами, умова eij <0, зазвичай виконується. У випадку ж, коли серед величин eij зустрічаються і позитивні значення, можна перейти до строго негативних значень за допомогою перетворення eij - a при придатним чином підібраному a > 0. При цьому оптимальний варіант рішення залежить від а. Правило вибору відповідно до критерію Гермейєра формулюється в такий спосіб:
матриця рішень доповнюється ще одним стовпцем, що містить у кожнім рядку найменший добуток наявного в ній результату на імовірність відповідного стану Fj. Вибираються ті варіанти, в рядках яких знаходиться найбільше значення eij цього стовпця. У деякому змісті критерій Гермейєра узагальнює критерій Вальда: у випадку рівномірного розподілу qj = Умови його застосування такі: 1) імовірності появи станів Fj невідомі; 2) з появою тих чи інших станів окремо чи у комплексі, необхідно рахуватися; 3) допускається деякий ризик; 4) рішення може реалізуватися один чи кілька разів. Якщо функція розподілу відома не дуже надійно, а кількість реалізацій є малою, то, при використанні критерію Гермейєра, одержують, взагалі кажучи, невиправдано великий ризик.
ЛІТЕРАТУРА
1. Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972.– 552 с. 2. Вентцель Е.С. Исследование операций: задачи, принципы, методология.– М.: Наука, 1988.– 208 с. 3. Черчмен У., Акоф Р., Арноф Л. Введение в исследование операций.– М.: Наука, 1967.– 488 с. 4. Раскин Л.Г. Анализ сложных систем и элементы теории оптимального управления.– М.: Советское радио, 1976.– 344 с. 5. Вітлинський В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування.– К.: КНЕУ, 2001.– 248 с. 6. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование (теория, методы и приложения).– М.: Наука, 1969.– 424 с. 7. Банди Б. Основы линейного программирования.– М.: Радио и связь, 1989.– 176 с.
8. Геронимус Б.Л. Экономико-математические методы в планировании на автомобильном транспорте.– М.: Транспорт, 1982.– 160 с. 9. Воркут А.И. Грузовые автомобильные перевозки.– К.: Вища школа, 1986.– 447 с. 10. Акулиничев В.М., Кудрявцев В.А., Корешков В.Н. Математические методы в эксплуатации железных дорог. – М.: Транспорт, 1981.– 223 с. 11. Смехов А.А. Математические модели процессов грузовой работы.– М.: Транспорт, 1982.– 256 с. 12. Бакаев А.А. Экономико-математические методы планирования и проектирования транспортных систем.– К.: Техника, 1973.– 220 с. 13. Кожин А. П. Математические методы в планировании и управлении грузовыми автомобильными перевозками.– М.: Высшая школа, 1971 – 304 с. 14. Лащених О.А., Кузькін О.Ф. Методи і моделі оптимізації транспортних процесів і систем. – Запоріжжя: ЗНТУ, 2006. – 435 с. 15. Калихман И.Д., Войтенко М.А. Динамическое программирование в примерах и задачах.– М.: Высшая школа, 1979.– 125 с. 16. Беллман Р. Динамическое программирование.– М.: ИЛ, 1960.– 400 с. 17. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования.– М.: Наука, 1965 – 418 с. 18. Математические методы в планировании и управлении: Сборник задач / С.А. Кулиш, С.Н. Воловельская, А.И. Жилин, А.С. Пилипенко.– К.: Вища школа, 1985.– 239 с. 19. Новиков О.А., Петухов С.И. Прикладные вопросы теории массового обслуживания.– М.: Советское радио, 1969.– 400 с. 20. Клейнрок Л. Вычислительные системы с очередями.– М.: Мир, 1979.– 600 с. 21. Саати Т. Л. Элементы теории массового обслуживания и ее приложения. – М.: Советское радио, 1971.– 509 с. 22. Падня В.А. Применение теории массового обслуживания на транспорте.– М.: Транспорт, 1968.– 208 с. 23. Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов.– М.: Высшая школа, 1976.– 392 с. 24. Оре О. Теория графов.– М.: Наука, 1968.– 490 с. 25. Сыроежин И.М. Азбука сетевых планов.– М.: Экономика, 1966.– 151 с. 26. Параубек Г.Э. Сетевое планирование и управление.– М.: Экономика, 1967.– 143 с. 27. Бороздин И.Г. Сетевое планирование и управление в строительстве.– М.: Стройиздат, 1972.– 288 с. 28. Крушевский А.В. Теория игр.– К.: Вища школа, 1977.– 214 с. 29. Воробьёв Н.Н. Основы теории игр. Бескоалиционные игры.– М.: Наука, 1984 – 495с. 30. Сильянов В.В. Теория транспортных потоков в проектировании дорог и организации дорожного движения.– М.: Транспорт, 1977.– 303 с. 31. Танаев В.С., Шкурба В.В. Введение в теорию расписаний. – М.: Наука, 1975.– 240 с. ДЛЯ НОТАТОК
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 1018; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.219.166 (0.043 с.) |
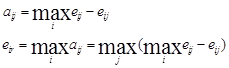
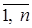 ) втратою у випадку вибору варіанта Ei.
) втратою у випадку вибору варіанта Ei. eij
eij
 aij
aij
 eir = { C
eir = { C  + (1-n)
+ (1-n) 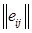 доповнюється стовпцем, складеним із середніх зважених (з вагою n º const) математичного очікування і найменшим результатом кожного рядка. Відбираються ті варіанти рішень у рядках якого стоїть найбільше значення цього стовпця.
доповнюється стовпцем, складеним із середніх зважених (з вагою n º const) математичного очікування і найменшим результатом кожного рядка. Відбираються ті варіанти рішень у рядках якого стоїть найбільше значення цього стовпця.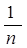 , j =
, j = 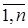 , вони стають ідентичними.
, вони стають ідентичними.


