
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамический режим сау. Уравнение динамикиСтр 1 из 8Следующая ⇒
Установившийся режим не является характерным для САУ. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от Рассмотрим САР, находящуюся в установившемся режиме, характеризующемся значением выходной величины y = yo. Пусть в момент t = 0 на объект воздействовал какой - либо возмущающий фактор, отклонив значение регулируемой величины. Через некоторое время регулятор вернет САР к первоначальному состоянию (с учетом статической точности) (рис.24). Если регулируемая величина изменяется во времени по апериодическому закону, то процесс регулирования называется апериодическим.
При резких возмущениях возможен колебательный затухающий процесс (рис.25а). Существует и такая вероятность, что после некоторого времени Тр в системе установятся незатухающие колебания регулируемой величины - незатухающий колебательный процесс (рис.25б). Последний вид - расходящийся колебательный процесс (рис.25в). Таким образом, основным режимом работы САУ считается динамический режим, характеризующийся протеканием в ней переходных процессов. Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ. Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики y(t) = F(u,f,t), описывающее изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений. Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так: F(y, y’, y”,..., y(n), u, u’, u”,..., u(m), f, f ’, f ”,..., f(k)) = 0.
В общем случае уравнение динамики оказывается нелинейным, так как реальные звенья САУ обычно нелинейны. В целях упрощения теории нелинейные уравнения заменяют линейными, которые приблизительно описывают динамические процессы в САУ. Получаемая при этом точность уравнений оказывается достаточной для технических задач. Процесс преобразования нелинейных уравнений в линейные называется линеаризацией уравнений динамики. Рассмотрим сначала геометрическое обоснование линеаризации.
В нормально функционирующей САУ значение регулируемой и всех промежуточных величин незначительно отличается от требуемых. В пределах малых отклонений все нелинейные зависимости между величинами, входящими уравнение динамики, могут быть приближенно представлены отрезками прямых линий. Например, нелинейная статическая характеристика звена на участке АВ (рис.26) может быть представлена отрезком касательной в точке номинального режима А"В". Начало координат переносится в точку О’, и в уравнениях записываются не абсолютные значения величин y,u,f, а их отклонения от номинальных значений: Математическое обоснование линеаризации состоит в том, что если известно значение f(a) какой - либо функции f(x) в любой точке x = a, а также значения производных от этой функции в данной точке f’(a), f”(a),..., f(n)(a), то в любой другой достаточно близкой точке x + Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем упрощенный, но наиболее характерный вариант уравнения динамики САУ: F(y,y',y",u,u') = f. Здесь производные по времени u',y',y" также являются переменными. В точке, близкой к номинальному режиму: f = fн +
В номинальном режиме, когда все отклонения и их производные по времени равны нулю, получаем частное решение уравнения: Fн = fн. Учитывая это и вводя обозначения получим: ao Отбрасывая все знаки aoy” + a1y’ + a2y = bou’ + b1u + cof
Отбрасывая все знаки В более общем случае: aoy(n) + a1y(n-1) +... + an - 1y’ + any = bou(m) +... + bm - 1u’ + bmu + cof При этом всегда нужно помнить, что в данном уравнении используются не абсолютные значения величин y, u, f их производных по времени, а отклонения этих величин от номинальных значений. Поэтому полученное уравнение будем называть уравнением в отклонениях. К линеаризованной САУ можно применить принцип суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход (рис.27). Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид: aoy(n) + a1y(n-1) +... + an - 1y’ + any = bou(m) +... + bm - 1u’ + bmu
Обычно n Для того, чтобы получить мат. описание системы, составляют мат. описание отдельных эл-тов системы. Мат. описание отдельных элементов системы составлено на основании физических законов, которые определяют процессы, протекающие в этих элементах.
ВОПРОС №3 Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности реальных возмущений. Во-первых, это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств. Во-вторых, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя Наиболее распространенными типовыми воздействиями являются: ступенчатое, импульсное и гармоническое воздействия. Любой сигнал u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий ui(t) и исследовать реакцию системы на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить результирующее изменение выходной величины y(t) суммируя полученные таким образом составляющие выходного сигнала yi(t). Особенно важное значение в ТАУ придают ступенчатому воздействию 1(t) = Зависимость изменения выходной величины системы от времени при подаче на ее вход единичного ступенчатого воздействия при нулевых начальных условиях называется переходной характеристикой и обозначается h(t).
Не менее важное значение в ТАУ уделяется импульсной переходной характеристике, которая описывает реакцию системы на единичное импульсное воздействие при нулевых начальных условиях, обозначают
h(t) – обратное преобразование Лапласа. Обратная задача: получив экспериментально динамич. хар-ку сис-мы в виде ее временной хар-ки можем определить передаточную ф-ию системы
ВОПРОС №4 Алгебраические критерии устойчивости
|
||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.211.66 (0.016 с.) |
 заданной величины. Процесс установления требуемого значения управляемой величины называется регулированием. Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.
заданной величины. Процесс установления требуемого значения управляемой величины называется регулированием. Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.
 Линеаризация уравнения динамики
Линеаризация уравнения динамики y = y - yн,
y = y - yн,  0 система находилась в номинальном режиме в состоянии покоя.
0 система находилась в номинальном режиме в состоянии покоя.
 .
. Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в функции F в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями, реле и т.п.
Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в функции F в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями, реле и т.п. m, так как при n < m САУ технически нереализуемы.
m, так как при n < m САУ технически нереализуемы.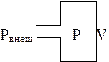 Пример: пневматическая (глухая) емкость – подключена к Рвнеш. Емкость имеет постоянный объем и считаем, что свойства воздуха подчинены свойствам идеального газа PV=GRT – ур-ие статики. Причины, которые могут вызывать изменение давления – изменение кол-ва воздуха(G) и температуры.
Пример: пневматическая (глухая) емкость – подключена к Рвнеш. Емкость имеет постоянный объем и считаем, что свойства воздуха подчинены свойствам идеального газа PV=GRT – ур-ие статики. Причины, которые могут вызывать изменение давления – изменение кол-ва воздуха(G) и температуры.  , R,V,T=const→
, R,V,T=const→ 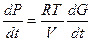 ,
,  ,
, 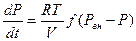 - обыкн. неоднородное диф. ур-ие I порядка.
- обыкн. неоднородное диф. ур-ие I порядка. при сложных изменениях входной величины.
при сложных изменениях входной величины. . Все остальные воздействия могут быть сведены к нему. Так, например, реальный импульсный сигнал может быть представлен двумя ступенчатыми сигналами одинаковой величины, но противоположными по знаку, поданными один за другим через интервал времени
. Все остальные воздействия могут быть сведены к нему. Так, например, реальный импульсный сигнал может быть представлен двумя ступенчатыми сигналами одинаковой величины, но противоположными по знаку, поданными один за другим через интервал времени  (t). Единичный импульс физически представляет из себя очень узкий импульс, ширина которого стремится к нулю, а высота - к бесконечности, ограничивающий единичную площадь. Математически он описывается дельта - функцией d(t) = 1’(t).
(t). Единичный импульс физически представляет из себя очень узкий импульс, ширина которого стремится к нулю, а высота - к бесконечности, ограничивающий единичную площадь. Математически он описывается дельта - функцией d(t) = 1’(t). Переходная и импульсная переходная характеристики называются временными характеристиками. Каждая из них является исчерпывающей характеристиками системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии. Другие названия этой хар-ки – переходная ф-ия, кривая разгона. Зная временную хар-ку, кот. м.б. определена либо экспериментально, либо аналитически, можно определить реакцию системы на вх. сигнал сложной формы, используя принцип суперпозиции(условие – система д.б. линейной). Допустим, что известна врем. хар-ка системы. Любой физически реализуемый сигнал м.б. представлен в виде лестничной ф-ии. Если взять некоторый шаг дискретизации времени, то для некоторого момента τк=к*1τ. Если Δτ достаточно мало, то Δf(τk)=(d f(τk)/dt)* Δτ. Вых. сигнал в любой момент времени будет определяться в соответствии с принципом суперпозиции как сумма р-ии на каждую отдельную ступеньку лестничной ф-ии
Переходная и импульсная переходная характеристики называются временными характеристиками. Каждая из них является исчерпывающей характеристиками системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии. Другие названия этой хар-ки – переходная ф-ия, кривая разгона. Зная временную хар-ку, кот. м.б. определена либо экспериментально, либо аналитически, можно определить реакцию системы на вх. сигнал сложной формы, используя принцип суперпозиции(условие – система д.б. линейной). Допустим, что известна врем. хар-ка системы. Любой физически реализуемый сигнал м.б. представлен в виде лестничной ф-ии. Если взять некоторый шаг дискретизации времени, то для некоторого момента τк=к*1τ. Если Δτ достаточно мало, то Δf(τk)=(d f(τk)/dt)* Δτ. Вых. сигнал в любой момент времени будет определяться в соответствии с принципом суперпозиции как сумма р-ии на каждую отдельную ступеньку лестничной ф-ии  Последнее выражение называется интегралом Дюамеля или интегралом свертки. Интеграл Дюамеля удобно применять при вычислении реакции линейной системы на вх. сигнал (апериодический), кот. задан либо графически, либо известно аналитическое выр-ие. Временная хар-ка представляет собой решение неоднородного линейного диф. ур-ия, характеризующее св-ва системы для единичного вх. сигнала при усл, что система до момента нанесения ступенчатого воздействия находилась в покое. Вх. сигнал имеет свое изображение
Последнее выражение называется интегралом Дюамеля или интегралом свертки. Интеграл Дюамеля удобно применять при вычислении реакции линейной системы на вх. сигнал (апериодический), кот. задан либо графически, либо известно аналитическое выр-ие. Временная хар-ка представляет собой решение неоднородного линейного диф. ур-ия, характеризующее св-ва системы для единичного вх. сигнала при усл, что система до момента нанесения ступенчатого воздействия находилась в покое. Вх. сигнал имеет свое изображение 
 , если сигнал ступенчатый, то
, если сигнал ступенчатый, то  . Изображение вых. сигнала можем получить как произведение передаточной функции системы на изображение вх. сигнала
. Изображение вых. сигнала можем получить как произведение передаточной функции системы на изображение вх. сигнала  - это решение неоднор. диф ур-ия в комплексной плоскости.
- это решение неоднор. диф ур-ия в комплексной плоскости. . Из св-в преобр. Лапласа следует, что
. Из св-в преобр. Лапласа следует, что  ,
,  .
. . Производную временной хар-ки принято называть импульсной переходной ф-ией. Если известна ИПФ, то вых. сигнал м.б. представлен в виде
. Производную временной хар-ки принято называть импульсной переходной ф-ией. Если известна ИПФ, то вых. сигнал м.б. представлен в виде  - интеграл свертки
- интеграл свертки


