Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Не содержит явным образом независимую переменную.
Уравнение этого вида допускает понижение порядка на единицу, если положить
……………………………………………….. Уравнение второго порядка, разрешенное относительно наивысшей производной, данного вида имеет вид
Рассмотрим его решение. Обозначим
Интегрируя это уравнение находим
Разделяя переменные, находим:
Интегрируя это уравнение, получим общий интеграл исходного уравнения:
Линейные однородные уравнения. Определения и общие свойства Определение. Дифференциальное уравнение п -го порядка называется линейным, если оно первой степени относительно искомой функции у и ее производных у ',..., у (п -1), у (п) т. е. имеет вид
где а 0, a 1, a 2, ...,ап и f (x) — заданные функции от х или постоянные, причем Установим некоторые основные свойства линейных однородных уравнений, ограничиваясь в доказательствах уравнениями второго порядка. Теорема 1. Если у 1и у 2— два частных решения линейного однородного уравнения второго порядка
то функция
— линейная комбинация решений у 1и у 2также решение этого уравнения. Доказательство. Так как у 1и у 2— решения уравнения, то
Подставляя в уравнение (44) сумму
т.е. Определение. Два решения уравнения (44) у 1и у 2называются линейно независимыми на отрезке
В противном случае решения называются линейно зависимыми. Иными словами, два решения у 1и у 2называются линейно зависимыми на отрезке
Определение. Если у 1и у 2суть функции от х,то определитель
называется определителем Вронского или вронскианом данных Теорема 2. Если функции у 1и у 2линейно зависимы на отрезке Действительно, если
Теорема 3. Если решения у 1и у 2уравнения (44) линейно независимы на отрезке Теорема 4. Если у 1и у 2— два линейно независимых на отрезке
есть его общее решение. Доказательство. Из теоремы 1 следует, что функция Докажем теперь, что каковы бы ни были начальные условия Так как
Равенства (47) представляют собой систему линейных алгебраических уравнений с неизвестными С 1и С 2 . Определитель этой системы
есть определитель Вронского при х = х 0и, следовательно, не равен 0 (в силу линейной независимости решений у 1и у 2). С 1и С 2 найдем применяя, например, формулы Крамера. Частное решение, которое получится из семейства (45) при найденных значениях С 1и С 2 , удовлетворяет заданным начальным условиям. Таким образом, теорема доказана. Замечание. Не существует общих методов для нахождения в конечном виде общего решения линейного уравнения с переменными коэффициентами. Однако для уравнения с постоянными коэффициентами такой метод существует. Он будет изложен в следующем пункте.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.193.207 (0.007 с.) |
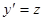 , где
, где  , тогда
, тогда  выражаются по формулам, основанным на правиле дифференцирования сложной функции:
выражаются по формулам, основанным на правиле дифференцирования сложной функции: ,
,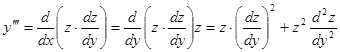 ,
,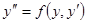 . (39)
. (39)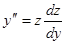 . Подставляя в уравнение (39) выражения
. Подставляя в уравнение (39) выражения 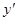 и
и  получим уравнение первого порядка, относительно функции
получим уравнение первого порядка, относительно функции 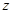 :
: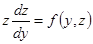 .
.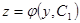 .
.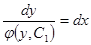 .
.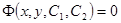 .
.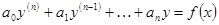 , (43)
, (43) для всех значений х из той области, в которой мы рассматриваем уравнение (43). В дальнейшем мы будем предполагать, что функции а 0, a 1, a 2, ...,ап и f (x) непрерывны на некотором интервале
для всех значений х из той области, в которой мы рассматриваем уравнение (43). В дальнейшем мы будем предполагать, что функции а 0, a 1, a 2, ...,ап и f (x) непрерывны на некотором интервале 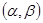 оси х,причем коэффициент а 0 = 1 (если он не равен 1, мы можем все члены уравнения поделить на него). Функция f (x), стоящая в правой части уравнения, называется правой частью уравнения. Если
оси х,причем коэффициент а 0 = 1 (если он не равен 1, мы можем все члены уравнения поделить на него). Функция f (x), стоящая в правой части уравнения, называется правой частью уравнения. Если  , то уравнение называется линейным однородным, в противном случае — линейным неоднородным.
, то уравнение называется линейным однородным, в противном случае — линейным неоднородным.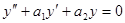 , (44)
, (44)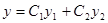 (45)
(45)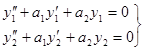 (46)
(46)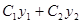 и принимая во внимание тождества (46), будем иметь:
и принимая во внимание тождества (46), будем иметь:
 , если их отношение на этом отрезке не является постоянным, т. е. если
, если их отношение на этом отрезке не является постоянным, т. е. если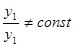 .
.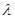 , что
, что 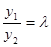 при
при  . В этом случае
. В этом случае  .
.
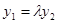 где
где  , то
, то 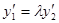 и
и .
.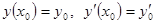 , где
, где 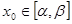 можно так подобрать значения произвольных постоянных С 1и С 2, чтобы соответствующее частное решение
можно так подобрать значения произвольных постоянных С 1и С 2, чтобы соответствующее частное решение  , то подставляя начальные условия, будем иметь:
, то подставляя начальные условия, будем иметь: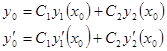 (47)
(47)