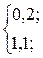Теорема: Проблема самоприменимости алгоритмически неразрешима.

Доказательство проводится от противного [7]. Допустим, что такая программа S существует, то есть она применима к записи любой программы и перерабатывает записи несамоприменимых программ, например, в 0, а самоприменимых в 1.

Если Р несамоприменима, то S((P))=0.

Если Р самоприменима, то S((P))=1.

Но тогда возможна и программа R:

Если Р несамоприменима, то R((P))=0.

Если Р самоприменима, то R((P))= неопределено.

То есть R применима к записям несамоприменимых программ и неприменима к записям самоприменимых. Такую программу R можно построить путем композиции S◦B программ S и В, где В:

B: 1)?

2) HLT.

Здесь В применима к нулевым словам и неприменима к единичным (не останавливается в этом случае).

Но сама R либо самоприменима, либо несамоприменима.

Тогда:

Если R несамоприменима, то R((R))=0.

Если R самоприменима, то R((R))= неопределено.

Получается, что если R несамоприменима, то R((R))=0, то есть, определено, что означает, что R самоприменима. Если R самоприменима, то R((R))= неопределено, т.е. R несамоприменима.

Итак, мы пришли к противоречию, основанному на допущении о том, что существует машина S, решающая проблему самоприменимости. Следовательно, такой машины не существует.

Заметим, что неразрешима именно массовая проблема: не существует единого алгоритма, который решал бы проблему самоприменимости. Это не говорит о том, что нет решения проблемы для конкретных машин. Так, для рассмотренных выше примеров машин Тьюринга такой алгоритм существует.

Используя результат, доказанный теоремой, можно доказать неразрешимость других алгоритмических проблем. Укажем, например, проблему применимости к начальному слову. Она состоит в следующем: указать алгоритм, который по машине М и слову Х устанавливал бы, применима машина М к слову Х или нет.

Проблема применимости к начальному слову также алгоритмически неразрешима, т.е. не существует машины Тьюринга, решающей эту проблему в указанном выше смысле.

Доказательство сводится к проблеме самоприменимости, которая неразрешима, как доказано выше.

Неразрешимости становятся бытом математики, и с их существованием приходится считаться [19]. С теоретической точки зрения, неразрешимость – не неудача, а научный факт. Знание основных неразрешимостей теории алгоритмов должно быть для специалиста по дискретной математике таким же элементом научной культуры, как для физика – знание о невозможности вечного двигателя. Если же важно иметь дело с разрешимой задачей (а для прикладных наук это стремление естественно), то следует четко представлять себе два обстоятельства. Во-первых (об этом уже говорилось при обсуждении проблемы остановки), отсутствие общего алгоритма, решающего данную проблему, не означает, что в каждом частном случае этой проблемы нельзя добиться успеха. Поэтому, если проблема неразрешима, надо искать ее разрешимые частные случаи. Во-вторых, появление неразрешимости – это, как правило, результат чрезмерной общности задачи (или языка, на котором описаны объекты задачи). Задача в более общей постановке имеет больше шансов оказаться неразрешимой.

Кроме понятий разрешимости и неразрешимости, вводится понятие сложности алгоритмов.

 

Сложность алгоритма

 

Сложность алгоритма отражает затраты, требуемые для его работы. Будем рассматривать временную сложность. Это функция, которая каждой входной длине n ставит в соответствие минимальное время, затрачиваемое алгоритмом на решение всех однотипных индивидуальных задач этой длины [24].

Из курса математического анализа известно, что функция f(n) есть О(g(n)), если существует константа с такая, что |f(n)|£c(g(n)) для всех n³0 [19].

O(n) – сложность порядка n, n – параметр исходных данных алгоритма. O(n²) – сложность порядка n². Сложность бывает минимальной, средней и максимальной.

Сложностью задачи называется сложность наилучшего алгоритма.

Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность равна О(Р(n)), где Р(n) – некоторая полиномиальная функция от входной длины n. Алгоритмы, для временной сложности которых не существует такой оценки, называются экспоненциальными.

Задача считается труднорешаемой, если для нее не существует разрешающего полиномиального алгоритма.

Итак, основные классы сложности таковы:

а) Полиномиальная сложность.

P(n) – полином от n.

O(P(n)) – сложность задач класса Р.

Полиномиальные задачи: степень полинома не зависит от n.

Например: O(P(n)) – линейная, O(P(n²)) – квадратичная, O(P(n³)) – кубическая.

Такие задачи легко решаются на ЭВМ.

б) Экспоненциальная сложность.

O(xⁿ) – класс Е – экспоненциальный.

Например: O(2ⁿ) – построение булеана, O(2²ⁿ) – нахождение всех переключательных функций от n переменных. При больших n задача становится практически нерешаемой.

в) NP сложные задачи [36].

Вспомним задачу коммивояжера из теории графов. Перебор всех маршрутов в графе из n вершин требует рассмотрения n! вариантов. Однако, n! растет даже быстрее, чем 2ⁿ.

В так называемом недетерминированном алгоритме (существует и недетерминированная машина Тьюринга) варианты выбираются случайным образом, тогда, если повезет, можно относительно быстро найти вариант, удовлетворяющий заданным ограничениям [36]. Такие задачи, имеющие недетерминированное решение, которое иногда удается найти за полиномиальное время называются NP-сложными (Nondeterministic Polynomial).

Преобладает мнение, что детерминированных алгоритмов решения таких задач не существует. Для сокращения перебора вариантов при решении таких комбинаторных задач (задач комбинаторной сложности) предлагаются различные способы «борьбы с перебором, борьбы с проклятием размерности» [9-10]. В эвристических алгоритмах используют для этого некоторую дополнительную информацию – эвристики, позволяющие находить решения, лишь на 10-15 % хуже оптимальных. Тем не менее, NP сложные задачи не имеют гарантированных оценок времени решения. Даже незначительное изменение исходных данных приводит к его резкому увеличению.

Поэтому иногда говорят, что проблема NP полна, что означает ничтожно малую вероятность существования эффективного (полиномиального) алгоритма.

В настоящее время активно развивается направление так называемых генетических алгоритмов. Это направление использует в борьбе с перебором вариантов опыт развития природы и человека. При этом применяется и соответствующая терминология: «популяция» – некоторое множество вариантов; «скрещивание» вариантов путем определенного комбинирования «хромосом особей» из исходной популяции и получение «потомков»; «эволюция» с целью получения лучших решений.