
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между двумя плоскостями ⇐ ПредыдущаяСтр 6 из 6
Дано: Р1 и Р2 – две плоскости;
Две плоскости, пересекаясь, образуют 4 двухгранных угла, равных попарно. Один из них равен углу между нормальными векторами. Обозначая один из этих углов через
Выбирая знак «+», получаем
Условие параллельности 2-х плоскостей Если плоскости параллельны, то их нормальные векторы коллинеарны:
Условие перпендикулярности 2-х плоскостей Если плоскости перпендикулярны, то их нормальные векторы перпендикулярны:
Кривые второго порядка Алгебраические уравнения второй степени относительно декартовой системы координат вида Ах2+2Вху+Су2+Dх+Еу+F=0 представляют собой кривые второго порядка: окружность, эллипс, гипербола, парабола. Эллипс Опр.: Эллипс - геометрическое место точек на плоскости, сумма расстояний от которых до 2 данных точек (называемых фокусами) есть величина постоянная и равна 2 а.
y
r2 r1 F2(-c,0) 0 x F1(c,0) x
Исследование формы эллипса т.к. х и у входят в уравнение в четных степенях, то график симметричен относительно осей координат. . A1,A2,B1,B2 – вершины эллипса; A1A2=2a – большая ось эллипса, a - большая полуось; В1В2=2b – малая ось, b – малая полуось;
Эксцентриситет эллипса и его влияние на форму Опр.: Эксцентриситет - отношение фокусного расстояния к большой оси
Директриса эллипса и фокальный радиус Директриса эллипса – это прямые, перпендикулярные большой оси эллипса и отстающие от центра на расстояние т.к. уравнение директрис
Гипербола Опр.: Гипербола – геометрическое место точек на плоскости, для каждой из которых модуль разности расстояний до 2 данных точек, называемых фокусами, есть величина постоянная и равна 2 a. у М(х,у) r2 r1
F2(-c,0) F1(c,0) х
Исследование формы гиперболы Т.к. х и у входят в уравнение в четных степенях, то график симметричен относительно координатных осей.
A1, A2 – вершины гиперболы 2 а – действительная ось гиперболы а – действительная полуось
2 b – мнимая ось гиперболы b – мнимая полуось
Асимптоты гиперболы Опр.: Прямая l называется асимптотой кривой с, если расстояние от точек кривой до прямой стремится к 0 при неограниченном удалении точек по кривой.
Покажем, что прямые
Эксцентриситет гиперболы, фокальные радиусы гиперболы Опр.: Эксцентриситет гиперболы – отношение фокусного расстояния к действительной оси.
Парабола Опр. Парабола – геометрическое место точек на плоскости, равноудаленных от данной точки - фокуса и от данной прямой - директрисы.
y N M(x,y)
B(
Пусть p - расстояние от фокуса до директрисы, т.е. BF=p, тогда, если ось ординат проходит через середину BF,то т. F имеет координаты ( Обозначим FM=r, a NM=d
Т.к. y входит в уравнение в четной степени, то график функции симметричен относительно OX. Если х=0, у=0 Если p >0, ветви вправо p <0, ветви влево
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.184.214 (0.013 с.) |

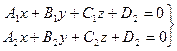
 - нормальный вектор плоскости Р1
- нормальный вектор плоскости Р1 - нормальный вектор плоскости Р 2
- нормальный вектор плоскости Р 2 , имеем:
, имеем:
 , выбирая знак «- «, получаем
, выбирая знак «- «, получаем 
 , следовательно, их координаты пропорциональны:
, следовательно, их координаты пропорциональны:
 , следовательно,
, следовательно, 





 y M(x,y)
y M(x,y)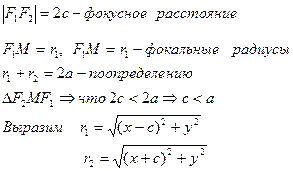




 - фокусное расстояние.
- фокусное расстояние. .
. =
= 


 , расстояние между директрисами
, расстояние между директрисами  ;
;




 -а а
-а а 
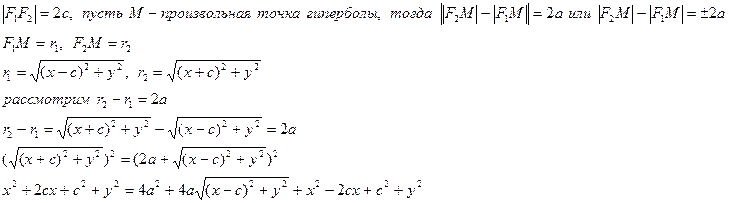
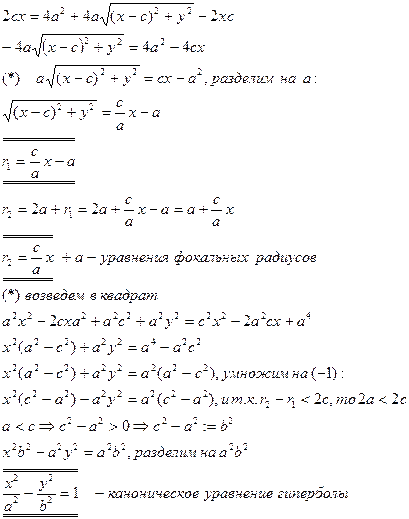



 являются асимптотами гиперболы.
являются асимптотами гиперболы.








 ) 0 x F(
) 0 x F(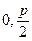 )
)



 - уравнение параболы
- уравнение параболы


