
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания по выполнению контрольных работСтр 1 из 7Следующая ⇒
Математический анализ
Методические указания Для студентов экономических специальностей
Красноярск 2004
УДК 512
Высшая математика: математический анализ (для студентов экономических специальностей заочной и вечерней форм обучения / Составитель О.В. Новоселов, Л.П. Скиба. Красноярск: СибГАУ, 2004. – 39 с.
© Сибирский государственный аэрокосмический университет, 2004 ОГЛАВЛЕНИЕ Указания по выполнению контрольных работ. 4 Программа курса «Высшая математика». 5 1. ВВЕДЕНИЕ В АНАЛИЗ.. 7 1.1. Функции. 7 1.2. Пределы.. 7 1.3. Непрерывность функции и точки разрыва. 11 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.. 13 2.1. Производные функции одной переменной. 13 2.2. Производные функции нескольких переменных. 16 2.3. Правило Лопиталя. 17 2.4. Исследование функции методами дифференциального исчисления. 19 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.. 23 3.1. Неопределенные интегралы.. 23 3.2. Определенные интегралы.. 28 3.3. Геометрические приложения определенных интегралов. 31 4. РЯДЫ... 33 4.1. Числовые ряды.. 33 4.2. Степенные ряды.. 36 ЛИТЕРАТУРА.. 39
Указания по выполнению контрольных работ Настоящие методические указания предназначены для студентов экономических специальностей, изучающих курс высшей математики по заочной форме обучения. Объём и содержание предлагаемого раздела «Математический анализ» определены программой курса, составленной в соответствии с ГОС Министерства образования РФ. Указанные указания не заменяют основную учебную литературу, а имеют своей целью помочь студенту-заочнику быстрее разобраться в материале, необходимом для выполнения контрольных работ и лучше усвоить наиболее сложные вопросы раздела. В указаниях приведены основные понятия и результаты, а также методика решения типовых задач изучаемого материала. Студент должен выполнять один тот же вариант всех контрольных работ. Чтобы определить свой вариант, нужно разделить на 25 число, полученное отсечением двух цифр от номер студенческого билета (шифра), обозначающих год поступления в университет. Остаток от деления и есть номер вашего варианта. Если остаток равен нулю, то номер вашего варианта равен 25. Например, если шифр студента равен 23602, тогда остаток от деления 236 на 25 будет равен 11 и, следовательно, решать нужно вариант №11; если шифр студента равен 57501, тогда остаток от деления 575 на 25 будет равен 0 и, следовательно, решать нужно вариант №25.
При выполнении контрольных работ необходимо соблюдать следующие правила: 1. В начале работы разборчиво написать свою фамилию, инициалы, шифр, номер и вариант контрольной работы и дату отсылки ее в университет. 2. Каждую контрольную работу выполнять в отдельной тетради (или на белой бумаге формата А4), авторучкой или распечатанной на принтере с полями не менее 3 см для замечаний рецензента. 3. Решения задач располагать в порядке номеров, указанных в контрольных работах. В начале каждого решения записывать условие задачи (без сокращений). 4. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов. Обязательно, если требуется, выполнять чертежи с пояснениями и нарисованными аккуратно. Контрольные работы, выполненные с нарушением изложенных правил или не своего варианта, не засчитываются и возвращаются без проверки. Получив прорецензированную работу, студент обязан исправить в ней отмеченные ошибки и недочеты. Если работа не зачтена, ее необходимо в короткий срок либо выполнить заново (целиком), либо переделать задачи, указанные рецензентом. Исправленную работу следует посылать в университет вместе с незачтенной. Зачтенные контрольные работы предъявляются преподавателю при защите перед зачетом или экзаменом.
Программа курса «Высшая математика» Для экономических специальностей, раздел «Математический анализ» Дифференциальное исчисление 1. Производная функции одной переменной. Физический и геометрический смысл производной. Эластичность и ее свойства. 2. Производные основных элементарных функций. Основные правила дифференцирования. Производная сложной и обратной функции. Логарифмическое дифференцирование. 3. Производная функции многих переменных. Частные производные. 4. Производные высших порядков функций одной и нескольких переменных. 5. Производные сложных функций многих переменных.
6. Производные функций, заданных неявно параметрически. 7. Теоремы о среднем: Ролля, Лагранжа, Коши. 8. Дифференциал функции одной переменной. Геометрический смысл дифференциала. Дифференциал функции нескольких переменных. Свойства дифференциалов. Применение дифференциала для приближенных вычислений и оценки погрешности вычислений. Дифференцируемость функций. Дифференциалы высших порядков. 9. Правило Лопиталя. 10. Необходимое условие экстремума функции. Необходимые и достаточные условия монотонности функции. Достаточные условия экстремума функции. 11. Наибольшее и наименьшее значение функции на заданном отрезке. 12. Выпуклость и вогнутость функции. Точки перегиба. Необходимое и достаточное условия существования точек перегиба. Асимптоты функции. Вертикальные и наклонные асимптоты и способы их нахождения. Общая схема исследования функции и построения её графика. Интегральное исчисление 1. Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов 2. Метод замены переменной и метод подведения под знак дифференциала вычисления неопределенных интегралов. 3. Метод интегрирования по частям вычисления неопределенных интегралов. 4. Алгебра многочленов. Основная теорема алгебры. Теорема Безу. Разложение многочлена на линейные и квадратные множители. 5. Разложение рациональных дробей на сумму простейших дробей. Метод неопределенных коэффициентов. 6. Интегрирование дробно-рациональных функций. Интегрирование простейших дробей 1-го, 2-го и 3-го типа. Интегрирование простейших выражений, содержащих квадратный трехчлен. 7. Интегрирование в тригонометрических выражений вида R(sin x,cos x). Универсальная подстановка. Интегрирование тригонометрических выражений вида cos mx sin nx. 8. Интегральные суммы. Определение определенного интеграла. Физический, геометрический и экономический смысл определенного интеграла. Свойства определенных интегралов. 9. Формула Ньютона-Лейбница и её применение для вычисления определённых интегралов. Метод замены переменной в определенном интеграле. Метод интегрирования по частям в определенном интеграле. 10. Применение определенного интеграла к вычислению площадей плоских фигур. 11. Несобственные интегралы 1-го и 2-го рода. Ряды 1. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости рядов. Свойства сходящихся рядов. 2. Ряды с положительными членами. Признаки сходимости знакоположительных рядов: признаки сравнения, признаки Даламбера и Коши, интегральный признак. 3. Знакопеременные ряды. Абсолютная и условная сходимости. Теорема Лейбница для знакочередующихся числовых рядов. 4. Функциональные ряды. Область сходимости, методы её определения. Равномерная сходимость. Свойства равномерно сходящихся рядов. 5. Степенные ряды. Терема Абеля. Радиус сходимости степенного ряда. 6. Разложение функций в степенные ряды. Формула Тейлора. 7. Формула Маклорена. Разложение основных элементарных функций в ряд Маклорена. 8. Применение степенных рядов в приближённых вычислениях.
ВВЕДЕНИЕ В АНАЛИЗ Функции Функция является основным объектом исследования в математическом анализе. Поэтому рекомендуем более глубоко ознакомиться с этим понятием, например, обратиться к литературе, приведенной в конце методических указаний.
При построении графика воспользуемся следующими правилами. Пусть известен график функции y = f (x), тогда график функции:
Отметим, что вместо смещения графиков вдоль координатных осей можно смещать сами оси координат, но только в противоположную сторону. Пример 1.1. Используя элементарные преобразования графиков, построить график функции y = 1–2cos3 x. Решение. График исходной функции можно построить в четыре этапа: 1) строим график синусоиды y 1=cos x; 2) сжимаем график в 3 раза вдоль оси Ox: y 2=cos3 x; 3) увеличиваем амплитуду синусоиды в 2 раза и переворачиваем график вокруг оси Ox на 1800: y 3=–2cos3 x; 4) смещаем график y 3 на 1 ед. вверх или опускаем ось Ox на 1 ед. вниз, в результате получим с графиком исходной функции y.
Пределы Понятие предела является одним из фундаментальных понятий математики. Для более глубокого ознакомления с этим понятием мы рекомендуем обратиться к литературе, приведенной в конце методических указаний. Пусть функция y=f (x) определена в некоторой окрестности точки a. Число A называется пределом функции f (x) при x ® a, если для любого сколь угодно малого e>0 существует такое d>0, что для всех x, удовлетворяющих неравенству | x–a |<d, имеет место неравенство | f (x)– A |<e. Обозначается
Аналогичные определения можно дать, когда a или A равны нулю или бесконечности. Функция a(x) называется бесконечно малой в окрестности точки a, если
Функция A (x) называется бесконечно большой в окрестности точки a, если
Свойства пределов 1. 2. 3. 4. 5. 6. При вычислении пределов
2) Функция f (x) не определена в предельной точке a. В этом случае мы будем иметь дело с т.н. неопределенностями: Раскрытие неопределенностей вида
Пример 1.2. Вычислить пределы: а) Решение. а) Здесь мы имеем с неопределенностью вида
б) Здесь мы имеем с неопределенностью вида ¥–¥. Умножим и разделим данное выражение на точно такое же, но со знаком плюс между слагаемыми (на сопряженное выражение):
В результате получилась неопределенность типа
Раскрытие неопределенностей вида
Пример 1.3. Вычислить пределы: а) Решение. а) Здесь мы имеем с неопределенностью вида
б) Здесь мы имеем с неопределенностью вида
Первый замечательный предел:
Из этого предела также вытекает
Второй замечательный предел:
Второй замечательный предел имеет место при неопределенности вида 1¥. Его также записывают в виде
Из второго замечательно предела вытекает
При вычислении пределов вида
В этом случае пишут a(x)~b(x). Тогда в вычислениях пределов вместо одной бесконечно-малой величины можно брать другую эквивалентную бесконечно-малую величину. Таблица эквивалентностей Пусть a(x) – бесконечно-малая величина в окрестности точки x 0. Тогда
Пример 1.4. Вычислить пределы:
Решение. Используя метод эквивалентных бесконечно-малых величин, получаем
При использовании второго замечательного предела воспользуемся следующим равенством:
где f (x)®0, g (x)®¥ при x ® x 0. Пример 1.5. Вычислить пределы: а) Решение. а) Здесь мы имеем с неопределенностью вида
Далее, используя равенство (1.1), получим
б) Здесь мы также имеем с неопределенностью вида
Учитывая (1.1), где
Решение. а)
б)
в) При вычислении производной по x, выражение в скобках будет константой. Поэтому при вычислении производной по x следует воспользоваться формулой
При вычислении производной по y, выражение в показателе будет константой. Поэтому при вычислении производной по y следует воспользоваться формулой
Правило Лопиталя Правило Лопиталя применяется для раскрытия неопределённостей типа
Пример 2.6. Вычислить пределы, используя правило Лопиталя:
Решение. а) Здесь имеется неопределенность вида
Поскольку неопределенность
б) Здесь имеется неопределенность вида
Поскольку неопределенность
Для раскрытия неопределенностей
В результате исходный предел будет равен
Пример 2.7. Вычислить пределы, используя правило Лопиталя:
Решение. а) Здесь имеется неопределенность вида
Рассмотрим последний предел
Ёще раз применим правило Лопиталя
Таким образом,
б) Здесь имеется неопределенность вида
Применим правило Лопиталя:
Ещё раз применяем правило Лопиталя:
Таким образом,
2.4. Исследование функции методами Если функция f (x) дифференцируема на (a, b) и Максимум и минимум функции называются экстремумом функции. Необходимое условие экстремума функции. Если дифференцируемая функция f (x) имеет в точке x 0 экстремум, то её производная в этой точке равна нулю или не существует. Точка x 0, в которой производная функции равна нулю или не существует, называется критической. Не всякая критическая точка является точкой экстремума. Достаточное условие экстремума функции. Если при переходе через критическую точку слева направо Пусть функция f (x) непрерывна на отрезке [ a, b ]. Такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке x 0 отрезка [ a, b ], либо на границе отрезка, т.е. при x = a или x = b. Если x 0Î(a, b), то точку x 0 следует искать среди критических точек данной функции. Правило нахождения наибольшего и наименьшего значений функции на [ a, b ]: 1) Найти критические точки функции на интервале (a, b). 2) Вычислить значения функции f (x) в найденных критических точках. 3) Вычислить значения функции f (x) на концах отрезка, т.е. в точках x=a и x=b. 4) Среди всех вычисленных значений функции f (x) выбрать наибольшее и наименьшее. Пример 2.8. Найти наибольшее и наименьшее значения функции
на отрезке [0;3]. Решение. Найдем производную:
Отсюда находим критические точки: x 1=2, x 2=4. Однако в заданный интервал попадает только одна точка: x 1=2Î[0;3]. Далее находим значение функции в найденной критической точке и на границах отрезка:
Итак, наибольшее значение рассматриваемая функция принимает на левом конце заданного отрезка: yнаиб = y (0) = 4, а наименьшее значение – в точке минимума: yнаим = y (2) = 0. Говорят, что кривая вогнутая на интервале (a, b), если она лежит выше касательной, проведенной в любой её точке. Говорят, что кривая выпуклая на интервале (a, b), если она лежит ниже касательной, проведенной в любой её точке. Достаточное условие выпуклости (вогнутости) графика функции. Если Точка кривой, отделяющая её выпуклую часть от вогнутой, называется точкой перегиба. При переходе через точку перегиба вторая производная меняет знак. Асимптотой кривой y=f (x) называется прямая, к которой приближается график функции при неограниченном удалении от начала координат. Различают асимптоты вертикальные, наклонные и горизонтальные. Прямая x=a называется вертикальной асимптотой кривой y=f (x), если при x ® a (слева или справа) значение функции стремится к бесконечности, т.е. выполнено одно из следующих условий:
Прямая y=kx+b является наклонной асимптотой кривой y=f (x), если существуют пределы:
Прямая y=b является горизонтальной асимптотой кривой y=f (x), если существует предел:
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Неопределенные интегралы Понятие интеграла, наряду с производной, является одним из основных в математическом анализе. Он играет большую роль в приложениях. Поэтому стоит более глубоко ознакомится с этим понятием по приведенной литературе. Функция F (x) называется первообразной функции f (x) на (a, b), если Совокупность всех первообразных
В этом равенстве f (x) называется подынтегральной функцией, а f (x) dx – подынтегральным выражением. Свойства неопределенных интегралов
Таблица простейших интегралов
Пример 3.1. Вычислить неопределенные интегралы:
Решение. а) Используя свойства 3 и 4, получим
Далее, используя из таблицы интегралов формулы 2 и 4, находим
Тогда
б) Используя свойство 5 и формулу 5, получим
в) Здесь используем формулу 3 с учётом свойства 5:
г) Запишем подынтегральную функцию следующим образом:
Тогда, с чётом формулы 12 и свойства 5, получаем
Метод замены переменной. Положим x =j(t), где j(t) – дифференцируемая функция. Учтём, что дифференциал вычисляется по формуле
Тогда справедлива следующая формула
Пример 3.2. Вычислить неопределенные интегралы, используя метод замены переменной: а) Решение. а) При вычислении первого интеграла сделаем подстановку t =5–9ln x, в результате получим
б) При вычислении второго интеграла сделаем подстановку t =5+4 x 10, в результате получим
Метод интегрирования по частям. Если u (x) и v (x) – дифференцируемые функции, то справедлива формула
Данную формулу интегрирования применяют обычно в тех случаях, когда функция u (x) упрощается при дифференцировании, а первообразная для функции v (x) легко находится. Пример 3.3. Вычислить неопределенные интегралы, используя метод замены переменной: а) Решение. а) При вычислении первого интеграла воспользуемся формулой интегрирования по частям:
б) При вычислении второго интеграла также воспользуемся формулой интегрирования по частям. В результате получим
Дробно-рациональной функцией (или рациональной дробью) называется выражение
Если n ³ m, дробь называется неправильной. Если n < m, дробь называется правильной. Любую неправильную рациональную дробь можно представить в виде суммы целой части (т.е. многочлена) и правильной дроби. Пример 3.4. Вычислить интеграл:
Решение. Выделим целую и дробную части рациональной дроби, для этого разделим столбиком два многочлена (числитель на знаменатель):
В результате получаем
Любую правильную рациональную дробь можно представить в виде суммы простейших дробей вида:
Чтобы правильную рациональную дробь представить в виде суммы простейших дробей, нужно сначала знаменатель разложить линейные и квадратичные множители вида (x+a) и Пример 3.5. Вычислить интеграл:
Решение. Разложим подынтегральную функцию, т.е. правильную рациональную дробь, на сумму простейших дробей:
Приведем правую часть равенства к общему знаменателю и приравняем числители левой и правой частей:
Чтобы найти неопределенные коэффициенты A, B, C, придадим переменной x три каких-либо значения (обычно выбирают такие значения, чтобы получались нулевые значения в правой части):
Таким образом,
Далее вычисляем исходный интеграл как сумму интегралов от простейших дробей:
При вычислении интегралов вида
следует преобразовать подынтегральную функцию, используя различные тригонометрические формулы. Если хотя бы одно из чисел m или n – нечётное положительное, то применяют подстановку cos x = t, если n – нечётное и sin x=t, если m – нечётное. При этом используется основное тригонометрическое тождество:
Пример 3.6. Вычислить интеграл:
Решение. Применяем подстановку sin x=t, cos xdx=dt:
Если m или n – чётные положительные числа, то применяются тригонометрические формулы понижения степени:
Пример 3.7. Вычислить интеграл:
Решение. Преобразуем подынтегральное выражение следующим образом
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.253.161 (0.271 с.) |

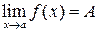 .
.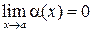 .
. .
. ,
,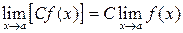 ,
,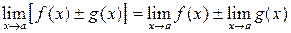 ,
,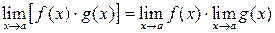 ,
,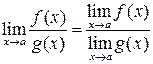 , если
, если 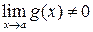 ,
,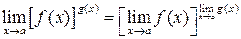 .
.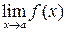 встречаются два случая.1) Функция f (x) определена в предельной точке a, тогда
встречаются два случая.1) Функция f (x) определена в предельной точке a, тогда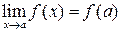 .
.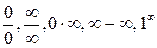 и т.п. Раскрытие (устранение) неопределенностей составляется основное содержание предлагаемых задач.
и т.п. Раскрытие (устранение) неопределенностей составляется основное содержание предлагаемых задач.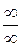 . Рассмотрим пределы вида
. Рассмотрим пределы вида  , где P (x) и Q (x) – многочлены. В этом случае можно воспользоваться следующей теоремой: сумма конечного числа бесконечно больших функций различных порядков эквивалентна слагаемому высшего порядка.
, где P (x) и Q (x) – многочлены. В этом случае можно воспользоваться следующей теоремой: сумма конечного числа бесконечно больших функций различных порядков эквивалентна слагаемому высшего порядка.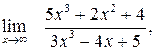 б)
б) 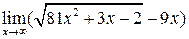 .
. . Тогда используя последнюю теорему, получим
. Тогда используя последнюю теорему, получим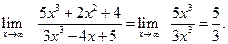
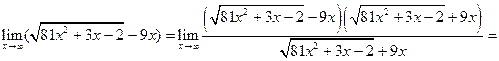
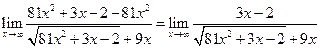 .
. .
. . Рассмотрим пределы вида
. Рассмотрим пределы вида 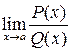 , где P (x) и Q (x) – многочлены. В этом случае числитель и знаменатель можно разложить на множители
, где P (x) и Q (x) – многочлены. В этом случае числитель и знаменатель можно разложить на множители .
. б)
б)  .
. . Разложим данное выражение на множители, а затем сократим дробь на x –1¹0 (x ®1, но x ¹1):
. Разложим данное выражение на множители, а затем сократим дробь на x –1¹0 (x ®1, но x ¹1):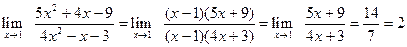 .
.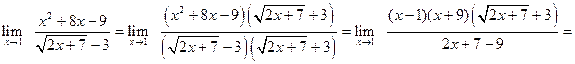
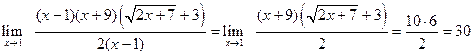 .
.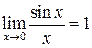 . (1.1)
. (1.1) ,
, 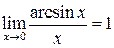 ,
, 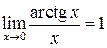 . (1.2)
. (1.2)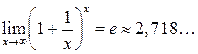 . (1.3)
. (1.3)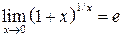 . (1.4)
. (1.4)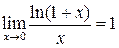 ,
, 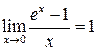 . (1.5)
. (1.5)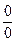 можно использовать метод эквивалентных бесконечно малых величин. Две бесконечно малые величины a(x) и b(x) называются эквивалентными в окрестности точки x 0, если
можно использовать метод эквивалентных бесконечно малых величин. Две бесконечно малые величины a(x) и b(x) называются эквивалентными в окрестности точки x 0, если .
.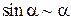 ,
,
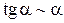 ,
,
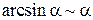 ,
,
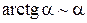 ,
,
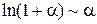 ,
,
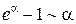 .
.
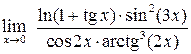 .
.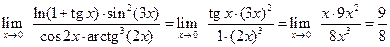 .
.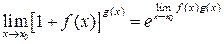 , (1.6)
, (1.6) б)
б) 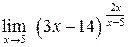 .
.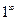 . Преобразуем выражение в скобках
. Преобразуем выражение в скобках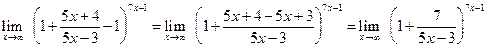 .
.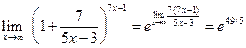 .
.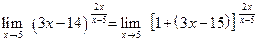 .
.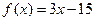 и
и 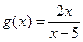 , получим
, получим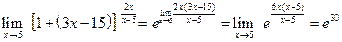 .
.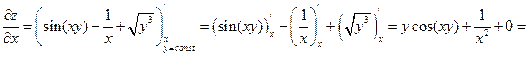
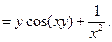

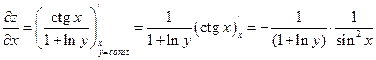 .
.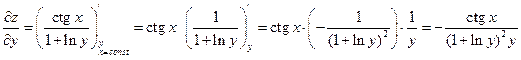 .
.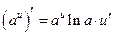 :
: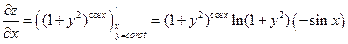 .
.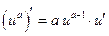 :
: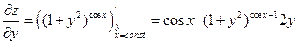 .
.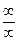 . Пусть при x ® a функции f (x) и g (x) обе бесконечно малые или бесконечно большие. Тогда предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует (в указанном смысле):
. Пусть при x ® a функции f (x) и g (x) обе бесконечно малые или бесконечно большие. Тогда предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует (в указанном смысле):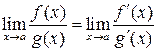 . (2.5)
. (2.5)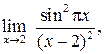
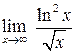 .
.
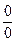 , поэтому можно применить правило Лопиталя:
, поэтому можно применить правило Лопиталя: .
.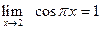 :
: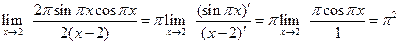 .
.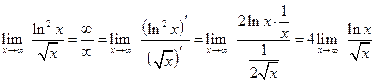 .
.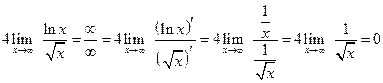 .
. , т.е. для вычисления пределов вида
, т.е. для вычисления пределов вида 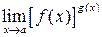 , нужно выражение, стоящее под знаком предела, сначала прологарифмировать, а затем уже вычислить предел полученного выражения:
, нужно выражение, стоящее под знаком предела, сначала прологарифмировать, а затем уже вычислить предел полученного выражения: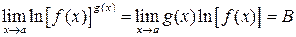 .
.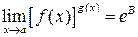 .
.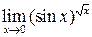 ,
,
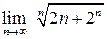 .
.
 . Пусть
. Пусть 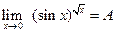 . Тогда
. Тогда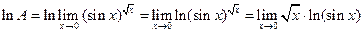 .
.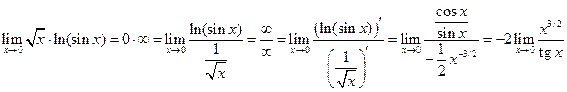 .
. .
.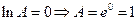 , т.е.
, т.е.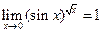 .
.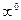 . Пусть
. Пусть  . Тогда
. Тогда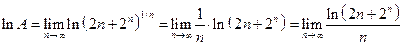 .
.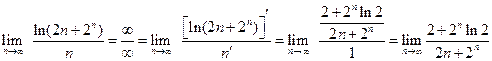 .
.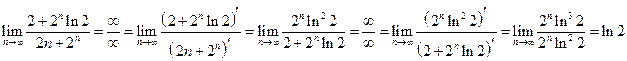 .
.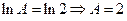 , т.е.
, т.е.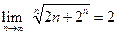 .
.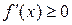 (или
(или  ), то функция f (x) не убывает (не возрастает) на (a, b).
), то функция f (x) не убывает (не возрастает) на (a, b).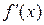 меняет знак с «+» на «–», то эта точка есть точка максимума функции, а если
меняет знак с «+» на «–», то эта точка есть точка максимума функции, а если 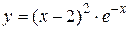
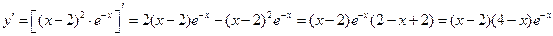 .
.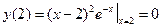 ,
, 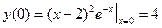 ,
, 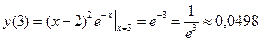 .
.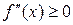 на (a, b), то график функции является вогнутым на этом интервале; если
на (a, b), то график функции является вогнутым на этом интервале; если  на (a, b), то график функции является выпуклым на этом интервале
на (a, b), то график функции является выпуклым на этом интервале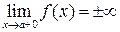 ,
, 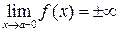 .
. ,
, 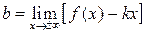 . (2.6)
. (2.6)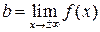 .
.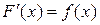 для любого
для любого 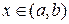 . Если F 1(x) и F 2(x) две первообразные функции f (x), то
. Если F 1(x) и F 2(x) две первообразные функции f (x), то 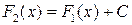 , т.е. любые две первообразные одной и той же функции отличаются друг от друга на постоянную величину.
, т.е. любые две первообразные одной и той же функции отличаются друг от друга на постоянную величину.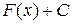 функции f (x) называется неопределенным интегралом от функции f (x) и обозначается символом
функции f (x) называется неопределенным интегралом от функции f (x) и обозначается символом  , т.е.
, т.е. . (3.1)
. (3.1)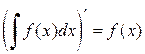 ,
,
 ,
,
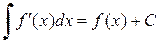 ,
,
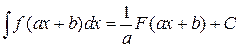 .
.
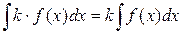 ,
,
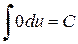 ,
,
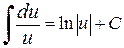 ,
,
 , a ¹1,
, a ¹1,
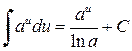 ,
,
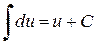 ,
,
 ,
,
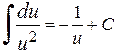 ,
,
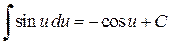 ,
,
 ,
,
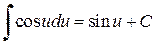 ,
,
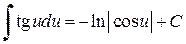 ,
,
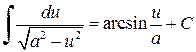 ,
,
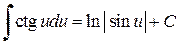 ,
,
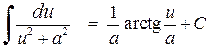 ,
,
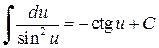 ,
,
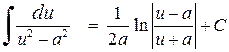 ,
,
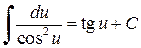 ,
,
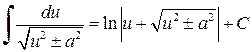 .
.
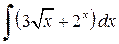 ,
,
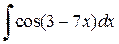 ,
,
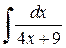 ,
,
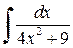 .
.
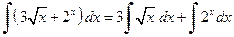 .
.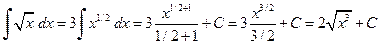 ,
, 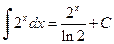 .
.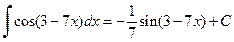 .
.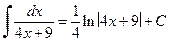 .
.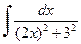 .
.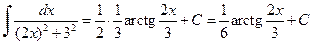 .
.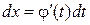 .
.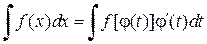 . (3.2)
. (3.2)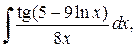 б)
б)  .
.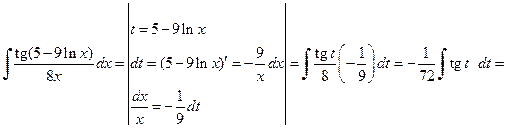
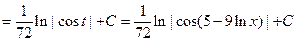 .
.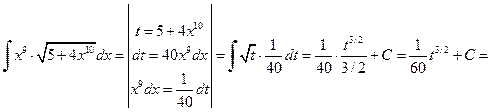
 .
.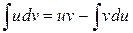 . (3.3)
. (3.3) б)
б) 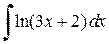 .
.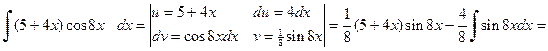
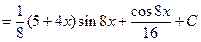 .
.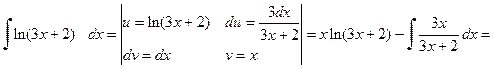
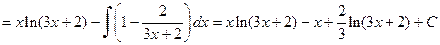 .
.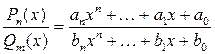 .
.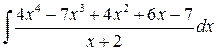 .
.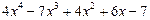
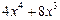
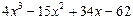


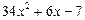
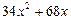
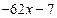
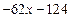
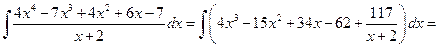
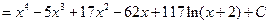 .
. ,
,
 ,
,
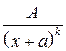 ,
,
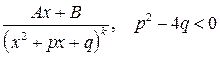 .
.
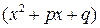 . В зависимости от полученных множителей получается соответствующее разложение на сумму простейших дробей. Рассмотрим этот метод на конкретном примере.
. В зависимости от полученных множителей получается соответствующее разложение на сумму простейших дробей. Рассмотрим этот метод на конкретном примере.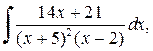 .
. .
.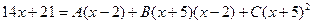 .
.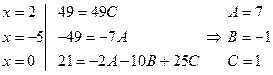
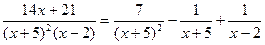 .
.
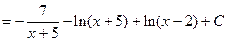 .
.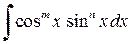 ,
, . (3.4)
. (3.4)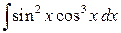 .
.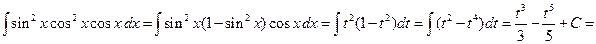
 .
.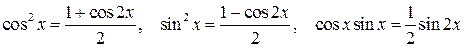 . (3.5)
. (3.5)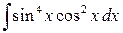 .
.


