
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы замены проективных координат на плоскости.
Рассмотрим на плоскости два проективных репера R = { A 1, A 2, A 3, E } и R ¢= { A ¢1 , A ¢2, A ¢3 , E ¢}. Пусть M Î – произвольная точка, и M (x 1, x 2, x 3) R, M (x ¢1, x ¢2, x ¢3) R¢. Будем писать коротко: M (xi) R, M (x ¢ i) R¢. Согласно определению 2.3.4., xi – это координаты некоторого вектора на прямой OM в некотором базисе B = {, , }, а x ¢ i – это координаты некоторого вектора на той же прямой OM в другом базисе B ¢ ={, , }. Поскольку векторы и должны быть коллинеарны, то = l и (l xi) B. Разложим векторы базиса B ¢ по базису B: = cki. Тогда матрица C = [ cik ], i, k = 1, 2, 3 называется матрицей перехода от базиса B к базису B ¢. Как известно, det C ¹ 0 и координаты l xi и x ¢ i вектора в различных базисах связаны формулами: l xi = cikx ¢ k. (2.6.1) эти же формулы показывают связь проективных координат xi и x ¢ i одной и той же точки в разных реперах на плоскости. В частности, поскольку в репере R ¢ A ¢1(1, 0, 0), A ¢2(0,1, 0), A ¢3(0, 0, 1), E ¢(1, 1, 1), то в репере R : A ¢1(c 11, c 21, c 31), A ¢2(c 12, c 22, c 32), A ¢3(c 13, c 23, c 33), E ¢(c 11+ c 12+ c 13, c 21+ c 22+ c 23, c 31+ c 32+ c 33). Замечание 1. Формулы (2.6.1) имеют место и для преобразования координат точек на прямой, при условии, что индексы i, k принимают значения 1, 2. Замечание 2. Если обозначить X и X ¢ – столбцы составленные из координат векторов и, то формулы (2.6.1) можно переписать в виде одного матричного равенства: l X = CX ¢ (2.6.1¢).
Уравнение прямой на плоскости. Пусть на проективной плоскости даны две точки A и B, имеющие в проективном репере R координаты A (a 1, a 2, a 3), B (b 1, b 2, b 3). Требуется составить уравнение прямой AB.
компланарны. И обратно, если компланарен и, то M Î l. Поэтому M Î AB Û
a 1 a 2 a 3= 0, (2.7.1) b 1 b 2 b 3 Это и есть уравнение прямой AB. После раскрытия определителя получим уравнение вида u 1 x 1 + u 2 x 2 + u 3 x 3 = 0. (2.7.2) Числа u 1, u 2, u 3 называются координатами прямой. Кроме того, условие коллинеарности векторов,, можно записать так: = l + l
x 2 = l a 2 + m b 2, (2.7.3) x 3 = l a 3 + m b 3, где l, m Î R – произвольные параметры (l2 + m2 ¹ 0). Эти уравнения называются параметрическими уравнениями прямой.
Следствие. Три точки A (a 1, a 2, a 3), B (b 1, b 2, b 3), C (c 1, c 2, c 3) лежат на одной прямой тогда и только тогда, когда существуют l, m Î R такие, что
c 2 = l a 2 + m b 2, (2.7.3) c 3 = l a 3 + m b 3.
Теорема Дезарга. Опр. 2.8.1. Трехвершинником на плоскости наз. фигура, которая состоит из трех точек, которые не лежат на одной прямой, и трех прямых, которые проходят через эти точки. Точки наз. вершинами, а прямые – сторонами трехвершинника. Пусть ABC и A ¢ B ¢ C ¢ – два трехвершинника. Будем наз. соответственными вершины A и A ¢, B и B ¢, C и C ¢, а также стороны a = BC и a ¢ = B ¢ C ¢, b = AC и b ¢ = A ¢ C ¢, c = AB и c ¢ = A ¢ B ¢. Теорема Дезарга. Если соответственные стороны трехвершинников ABC и A ¢ B ¢ C ¢ пересекаются в точках M, N, P, лежащих на одной прямой, то прямые, соединяющие соответственные вершины, сходятся в одной точке.
точке, то соответственные стороны этих трехвершинников пересекаются в точках, лежащих на одной прямой.
si = l ai +l¢ a ¢ i, si = m bi + m¢ b ¢ i, si = n ci + n¢ c ¢ i, i =1, 2, 3. Þ
Þ m bi – n ci = n¢ c ¢ i – m¢ a ¢ i = mi, n ci – l ai = l¢ a ¢ i – n¢ c ¢ i = ni, i =1, 2, 3,
32 Определение проективного преобразования. Опр. 3.1.1. Пусть и – две проективные плоскости, R – проективный репер в, R ¢ – в. Проективным отображениемна назы-вается отображение, действующее по правилу: точка M Î c координатами (x 1, x 2, x 3) в репере R переходит в точку M ¢Î с теми же координатами в репере R ¢.
Отсюда, в частности, вытекает, что A 1 переходит в A ¢1 , A 2– в A ¢2, A 3– в A ¢3, E – в E ¢, т.е R переходит в R ¢. Можно показать, что проективным отображением будет перспективное отображение на, которое возникает при центральном проецировании на, а также любая композиция перспективных отображений плоскости на плоскость. Опр. 3.1.2. Проективным преобразованием плоскости называется проективное отображение на себя. Оно задается двумя реперами R и R ¢ в плоскости. Движение, подобие и аффинное преобразование плоскости являются частными случаями проективных преобразований. 3.2. Формулы проективного преобразования. Пусть f : ® – проективное преобразование, которое задается двумя реперами R и R ¢, а С – матрица перехода от первого репера ко второму. Пусть M ¢ = f (M). Найдем связь между координатами M и M ¢ в одном репере, например, в R. Пусть M (x 1, x 2, x 3) R, тогда M ¢ имеет такие же координаты, только относительно R ¢. Пусть M ¢(x ¢1, x ¢2, x ¢3) R. Мы видим, что задача сводится к нахождению связи между координатами одной и той же точки M ¢ в разных реперах R и R ¢, а эта связь задается формулами (2.6.1). Значит, l x ¢ i = cikxk, i = 1, 2, 3. (3.2.1) Еще раз подчеркнем, что здесь xk – это координаты точки до преобразования, а x ¢ i – координаты образа этой точки. Замечание. Проективное преобразование точек прямой определяется аналогично, т.е. с помощью двух реперов R = { A 1, A 2, E }, R ¢= { A ¢1, A ¢2, E ¢} на этой прямой и состоит в том, что точка M (x 1: x 2) R переходит в M ¢(x 1: x 2) R ¢. Формулы преобразования имеют вид (3.2.1), где i, k = 1, 2. Формулы проективных преобразований записываются в матричном виде: l X ¢= CX. И каждому проективному преобразованию соответствует своя невырожденная матрица C.
33 Основное свойство проективных преобразований. Теор 3.3.1. При проективном преобразовании плоск-и прям переходит в прямую. Пусть преобразование задано реперами R и R ¢, а прямая имеет уравнение относительно R: u 1 x 1+ u 2 x 2 + u 3 x 3 = 0. Образ этой прямой будет удовлетворять такому же уравнению относительно R ¢, а значит, это тоже будет прямая. Опр. 3.4.1. Гомологией называется нетождественное проективное преобразование плоскости, имеющее точечно неподвижную (инвариант-ную) прямую, называемую осью гомологии. Свойства гомологии. 1. Прямая, проходящая через две несовпадающие соответственные точки, преобразуется в себя (является неподвижной). 2. Прямые, проходящие через несовпадающие соответственные точки (не принадлежащие одной прямой), проходят через одну неподвижную (инвариантную) точку, называемую центром гомологии. 3. Прямая, не проходящая через центр гомологии, и ее образ Перес-ся на оси гомологии. Опр. 3.4.1. Гомология, центр которой не принадлежит оси, наз. гиперболической. Гомология, центр которой принадлежит оси, наз. параболической. Гомология задается осью s, центром S и парой соответственных точек, лежащих на прям, проходящей через центр. Обозн.такую гомологиюG(S, s; A, A ¢). Соответственные при гомологии фигуры называются гомологичными. Примерами таких фигур являются трехвершинники из теоремы Дезарга. Фактически, теоремой Дезарга доказывается существование гомологии. Pисунок, 2.1, сопровождающий эту теорему, демонстрирует пример построения соответственных точек при гомологии G(S, s; A, A ¢), когда S –собственная точка.
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.110 (0.022 с.) |
 Пусть M – произвольная точка прямой AB. Ее координаты совпадают с координатами вектора на прямой OM. Координаты точек A и B также совпадают с координатами некоторых векторов и на прямых OA и OB. Значит, векторы, и
Пусть M – произвольная точка прямой AB. Ее координаты совпадают с координатами вектора на прямой OM. Координаты точек A и B также совпадают с координатами некоторых векторов и на прямых OA и OB. Значит, векторы, и x 1 x 2 x 3
x 1 x 2 x 3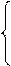 x 1 = l a 1 + m b 1,
x 1 = l a 1 + m b 1, c 1 = l a 1 + m b 1,
c 1 = l a 1 + m b 1, Обратная теорема Дезарга. Если прямые, соединяющие соответственные вершины трехвершинников ABC и A ¢ B ¢ C ¢, сходятся в одной
Обратная теорема Дезарга. Если прямые, соединяющие соответственные вершины трехвершинников ABC и A ¢ B ¢ C ¢, сходятся в одной Эти теоремы двойственные друг другу. Согласно принципу двойственности достаточно доказать одну из них, и тогда другая тоже будет верна. Мы докажем вторую теорему.
Эти теоремы двойственные друг другу. Согласно принципу двойственности достаточно доказать одну из них, и тогда другая тоже будет верна. Мы докажем вторую теорему. Пусть прямые AA ¢, BB ¢, CC ¢ имеют общую точку S. Пусть M = a I a ¢, N = b I b ¢, P = c I c ¢. Необходимо доказать, что M, N, P лежат на одной прямой. Для этого выберем на плоскости проективную систему координат, и запишем координаты точек A (ai), B (bi), C (ci), A ¢(a ¢ i), B ¢(b ¢ i), C ¢(c ¢ i), S (si), i =1, 2, 3. Поскольку S лежит на AA ¢, BB ¢, CC ¢, то
Пусть прямые AA ¢, BB ¢, CC ¢ имеют общую точку S. Пусть M = a I a ¢, N = b I b ¢, P = c I c ¢. Необходимо доказать, что M, N, P лежат на одной прямой. Для этого выберем на плоскости проективную систему координат, и запишем координаты точек A (ai), B (bi), C (ci), A ¢(a ¢ i), B ¢(b ¢ i), C ¢(c ¢ i), S (si), i =1, 2, 3. Поскольку S лежит на AA ¢, BB ¢, CC ¢, то l ai – m bi = m¢ b ¢ i – l¢ a ¢ i = pi,
l ai – m bi = m¢ b ¢ i – l¢ a ¢ i = pi, где pi, mi, ni – координаты точек P, M, N. Сложив эти равенства, получим pi + mi + ni = 0. Это значит, что P, M, N лежат на одной прямой s.
где pi, mi, ni – координаты точек P, M, N. Сложив эти равенства, получим pi + mi + ni = 0. Это значит, что P, M, N лежат на одной прямой s.


