
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стохастические оптимальные системы
В стохастических системах управления невозможно предсказать ход протекания процесса по известным управлению и начальному состоянию, так как он зависит еще и от случайных воздействий. Поэтому возможности управления такими системами существенно зависят от информации, получаемой путем измерения и обработки выходной переменной. Задача синтеза стохастической оптимальной системы в общем случае ставиться следующим образом. Задаются дифференциальные уравнения объекта, ограничения, краевые условия, уравнения наблюдения, критерий оптимальности и характеристически случайных воздействий и параметров. Требуется найти управление как функцию от измеренных значений выходной переменной y(t) на интервале t0£ t £ t. Для решения стохастических задач оптимального управления разработаны методы синтеза, основанные на сведении стохастических задач оптимального управления к задачам оптимальной оценки состояния и синтеза детерминированной оптимальной системы управления. 1.5.1.Метод динамического программирования Пусть объект описывается уравнением
где V0 (t) - белый шум с характеристиками
При условии, что
принимает минимальное значение. Итак, случайное воздействие является белым шумом и входит в уравнение объекта аддитивно; ограничение на правый конец траектории отсутствует, фазовый вектор измеряется полностью и без помех. В этой задаче Кроме того, предполагается, что уравнение
при каждом фиксированном Пусть в момент времени t фазовый вектор X(t) принимает определенное значение. Обозначим
Минимальное значение этого функционала
по определению есть функция Беллмана. Представим функцию Беллмана в виде
или
Используем свойство условного математического ожидания
Учитывая это свойство, можно записать
Подставив это выражение в (1.299) и используя принцип оптимальности, получим
Преобразуем последнее слагаемое
Следовательно,
Представим (1.296) в виде разностного уравнения
Если
Моменты более высокого порядка являются малыми величинами более высокого порядка, чем
Разлагая
Подставим это выражение в (1.300) и предельным переходом при
Если множество U(t) открыто и минимум левой части уравнения (1.302) достигается в стационарной точке, то уравнение Беллмана можно представить в виде следующей системы уравнений:
Достаточное условие оптимальности. Пусть существует скалярная функция Обычно уравнение Беллмана записывают, используя след матрицы
Поскольку
то уравнение (1.302) можно представить в виде
1.5.2.Синтез оптимальной системы при полной информации о состоянии Рассмотрим стохастическую задачу оптимального управления линейным объектом при квадратичном критерии и полной информации о состоянии системы:
и где V0 - белый шум с характеристиками
x0 - случайная величина с характеристиками
F, Q - неотрицательно-определенные симметричные матрицы; R - положительно-определенная симметричная матрица. Задача заключается в определении оптимального закона управления. Критерий оптимальности (11) имеет такой же смысл, что и критерий оптимального управления в детерминированной задаче. Здесь только производится усреднение по всем случайным факторам.
Для получения оптимального управления воспользуемся методом динамического программирования. Уравнения (1.303) в данном случае имеют следующий вид
После дифференцирования по управлению, получим:
Тогда, оптимальный закон управления имеет вид:
Подставим это выражение в первое уравнение
Решение этого уравнения будем искать в виде квадратичной формы
где К(t) - симметричная матрица; К0(t) - скалярная функция.
Подставим полученные выражения в последнее уравнение
после преобразований получим
Так как K – симметричная матрица, то
Выражение (15) называют матричным уравнением Риккати.
Тогда:
Граничное условие
принимает вид
поэтому
Подставив выражение для S в (1.309), получим оптимальный закон управления
Из определения функции Беллмана следует, что
Вычислим математическое ожидание от квадратичной формы:
Учитывая, что
где a, b - произвольные векторы одного размера, то получим
Для второго слагаемого правой части уравнения (1.313) из уравнения (1.310) с учетом граничного условия (1.311) (K0(tf) = 0) имеем
поэтому из (18) получаем
1.5.3.Синтез оптимальных систем управления при неполной информации Измерение (наблюдение) всегда сопровождается помехами, и состояние системы никогда точно неизвестно. Задача синтеза при этом намного сложнее, и для ее решения используют эвристический прием-метод разделения, при котором стохастическая задача синтеза при неполной информации разделяется на две задачи: задачу оптимальной оценки состояния; детерминированную задачу синтеза при неполной информации. В общем случае синтезированная таким способом система не обязательно является оптимальной. Однако, например, при линейных уравнениях объекта и наблюдение и среднеквадратичном критерии, метод позволяет синтезировать оптимальную систему. Таким образом, с задачей оптимального управления тесно связана задача оптимальной оценки. Наблюдатель Калмана-Бьюси Рассмотрим следующую задачу оптимального оценивания (наблюдения). Пусть объект и наблюдение описываются уравнениями
где V0 , VH - гауссовские белые шумы с характеристиками
x0 - гауссовская случайная величина с характеристиками
Q0, P0 - неотрицательно-определенные симметричные матрицы. R0 - положительно-определенная симметричная матрица. Случайные процессы Требуется, используя измеренные значения выходной переменной y(t) на интервале
Условие R0>0 означает, что ни одна компонента выходной координаты y(t) не измеряется точно. В этом случае задача оценивания называется несингулярной. Несмещенная оптимальная оценка x(t) определяется из уравнения
где матрица коэффициентов усиления
P - дисперсионная матрица ошибки
Если шумы объекта и наблюдения не коррелированы (
Несингулярная задача оценивания при некоррелированных шумах впервые была решена Р. Каллманом и Бьюси. Ее решение представляет собой оптимальный наблюдатель и называется наблюдателем (оценивателем) или чаще фильтром Каллмана - Бьюси.
Сравнивая уравнение объекта (1.316) и оптимального наблюдателя (1.319), замечаем, что их правые части отличаются только последними слагаемыми: в уравнении наблюдателя вместо шума объекта появляется слагаемое, пропорциональное разности Структурная схема наблюдателя Калмана - Бьюси включает в себя как составную часть модель исходной системы. Ее отличие от заданной системы состоим в том, что она имеет дополнительную обрратную связь по невязке (рис.1.15) Наблюдатель Калмана - Бьюси имеет такую же структуру, что и наблюдатель полного порядка в детерменированном случае. Соотношения (1.319) - (1.321) определяют также решение задачи линейного оптимального оценивания, которая отличается от задачи оптимального оценивания (1.316) - (1.318) тем, что: - о законах распределения шумов и начального состояния никаких предположений не делается (не требуется, чтобы они были гауссовскими); - нужно найти оптимальный наблюдатель в классе линейных систем, т.е. если шумы V0, VH и начальное состояние не является гауссовскими, то наблюдатель Калмана-Бьюси является оптимальным только среди линейных наблюдателей (систем). Наблюдатель при цветном шуме объекта В случае, если шум объекта является цветным, уравнения (1.316), (1.317) представляют в виде
где VH - белый шум с характеристиками
x(1) - случайный вектор с характеристиками
x(2) - шум объекта. Предполагается, что шум объекта является цветным и удовлетворяет уравнению
где V0 - белый шум с характеристиками
x0(2) - случайный вектор с характеристиками
Введем обозначения
Тогда приведенные уравнения можно представить в виде
Шум объекта есть GV0 с интенсивностью GQ0GT, поэтому наблюдатель Калмана-Бьюси при цветном шуме объекта описывается теми же уравнениями (1.319) - (1.322), но при условии, что в дисперсионном уравнении вместо Q0 подставляется GQ0GT. При некоррелированных шумах V0 и VH имеем:
где матрица коэффициентов усиления
Наблюдатель Калмана-Бьюси при цветном шуме объекта помимо модели исходной системы включает еще модель формирователя (рис. 1.16).
При цветном шуме наблюдения задача линейного оптимального оценивания решается также преобразованием ее в задачу линейного оптимального оценивания с белыми шумами. Пусть объект и наблюдение описываются уравнениями
где V0 – белый шум с характеристиками
x0 - случайный вектор с характеристиками
z - шум наблюдение подчиняется уравнению
W- белый шум с интенсивностью R0 . Шумы V0 и W не коррелированны со случайным вектором x0, но могут быть коррелированны между собой:
Из (1.324), (1.325) получаем
Введем новый вектор наблюдения
После подстановки выражений для
где
В преобразованном уравнении наблюдения (1.327) шум VH является белым. Его называют обобщенным шумом наблюдения. Интенсивность R0(t) и взаимная интенсивность S0(t) определяются следующим образом:
Пример 1.22. Определить оптимальную оценку скалярной постоянной x, по измерениям До начала измерения известны следующие характеристики x:
Искомая величина и шум независимы. Уравнение
Наблюдатель Калмана-Бьюси описывается уравнением
где
Пример. 1.23. Найти оптимальную оценку по наблюдению
где VH - белый шум с интенсивностью r0. Уравнение и начальные условия
где x2 - стационарный случайный процесс с характеристиками
x10 - случайная величина с характеристиками.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.250 (0.118 с.) |
 , (1.296)
, (1.296)
 . (1.297)
. (1.297) и
и  , требуется найти допустимое управление
, требуется найти допустимое управление  , при котором критерий оптимальности
, при котором критерий оптимальности , (1.298)
, (1.298) является марковским процессом (так как случайное воздействие является белым шумом), и вся информация, используемая при определении характеристики будущего состояния объекта, содержится в
является марковским процессом (так как случайное воздействие является белым шумом), и вся информация, используемая при определении характеристики будущего состояния объекта, содержится в  является допустимым, если функция
является допустимым, если функция  кусочно-непрерывна и принимает значения из Ut.
кусочно-непрерывна и принимает значения из Ut. ,
, . Функции
. Функции  предполагаются непрерывными.
предполагаются непрерывными. значение функционала (1.298) при t0 = t, указанном значении X(t) и некотором фиксированном управлении
значение функционала (1.298) при t0 = t, указанном значении X(t) и некотором фиксированном управлении  :
: .
. ,
, , (1.299)
, (1.299)
 .
. .
.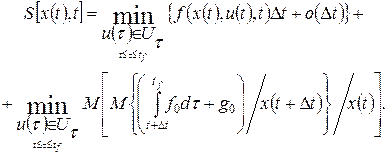
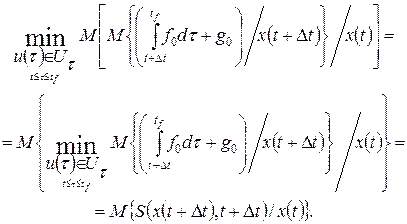
 . (1.300)
. (1.300) . (1.301)
. (1.301) - белый шум с характеристиками (1.297), то по определению белого шума
- белый шум с характеристиками (1.297), то по определению белого шума  является случайным процессом с характеристиками
является случайным процессом с характеристиками .
. , поэтому из (1.301) имеем
, поэтому из (1.301) имеем
 в ряд в точке
в ряд в точке  и используя последние соотношения, получим
и используя последние соотношения, получим
 получим
получим . (1.302)
. (1.302) , (1.303)
, (1.303) .
. , обладающая непрерывными частными производными S’t, S’x, S’’xx, и допустимое управление U*(x, t), удовлетворяющее уравнению Беллмана (1.302) или (1.303) и граничному условию
, обладающая непрерывными частными производными S’t, S’x, S’’xx, и допустимое управление U*(x, t), удовлетворяющее уравнению Беллмана (1.302) или (1.303) и граничному условию  . Тогда управление U*(x, t) является оптимальным.
. Тогда управление U*(x, t) является оптимальным.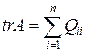 .
.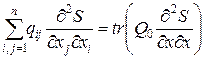 ,
, . (1.304)
. (1.304) , (1.305)
, (1.305) , (1.306)
, (1.306) , (1.307)
, (1.307) (1.308)
(1.308) .
. .
. . (1.309)
. (1.309) .
. ,
, ,
,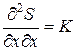 .
. .
. .
.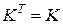 . Выражение
. Выражение 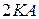 преобразуем к виду
преобразуем к виду  . Таким образом, получим:
. Таким образом, получим: . (1.310)
. (1.310) .
.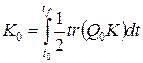 .
.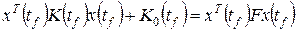 ,
, . (1.311)
. (1.311) . (1.312)
. (1.312) . (1.313)
. (1.313)
 ,
, .
. , (1.314)
, (1.314) . (1.315)
. (1.315) (1.316)
(1.316) , (1.317)
, (1.317) ,
, ,
, называются соответственно шумом объекта и шумом наблюдения или измерения. Они не коррелированы со случайной величиной x0.
называются соответственно шумом объекта и шумом наблюдения или измерения. Они не коррелированы со случайной величиной x0. , обеспечивающую минимум среднего квадрата ошибки:
, обеспечивающую минимум среднего квадрата ошибки: . (1.318)
. (1.318) , (1.319)
, (1.319) , (1.320)
, (1.320) и находится из дисперсионного уравнения
и находится из дисперсионного уравнения (1.321)
(1.321) ), то из (25), (26) следует
), то из (25), (26) следует ,
,
 . Эта разность между измеренным текущим значением выходной координаты и ее оценкой называется невязкой.
. Эта разность между измеренным текущим значением выходной координаты и ее оценкой называется невязкой.
 ,
,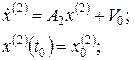
 .
.


 ,
,

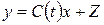 , (1.324)
, (1.324) , (1.325)
, (1.325)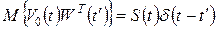 .
. .
. . (1.326)
. (1.326) и
и  получим
получим , (1.327)
, (1.327) (1.328)
(1.328) (1.329)
(1.329) , где V H(t) - белый шум с интенсивностью r0.
, где V H(t) - белый шум с интенсивностью r0. .
.

 ; p определяется из уравнения
; p определяется из уравнения

 ,
,




