
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные числовые характеристики дискретной случайной величины
Закон распределения случайной числовой величины характеризует ее полностью, но наиболее компактно можно выразить все существенные сведения о случайной величине, которыми мы располагаем, с помощью числовых параметров, получивших название числовых характеристик случайной величины, из которых рассмотрим математическое ожидание, дисперсию и среднеквадратическое отклонение. Определение. Математическим ожиданием называется сумма произведений всех возможных значений случайной величины на вероятности этих значений
Математическое ожидание соответствует тому значению случайной величины, около которого группируются все ее возможные значения. Математическое ожидание обладает следующими свойствами: 1. Математическое ожидание постоянной величины равно этой постоянной величине:
2. Постоянный множитель
3. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
5. Математическое ожидание отклонения случайной величины от ее математического ожидания всегда равно нулю:
Пример. Вычислить математическое ожидание дискретной случайной величины
Решение: Математическое ожидание дискретной случайной величины Х определяется как сумма произведений всех возможных значений случайной величины на их вероятности:
Определение. Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется дисперсией случайной величины
На практике широко применяется другая формула, значительно упрощающая процесс вычисления
Дисперсия случайной величины обладает следующими свойствами: 1. Дисперсия постоянной величины
2. Постоянный множитель
3. Если
Пример. Вычислить дисперсию дискретной случайной величины
Решение: Дисперсию удобно вычислять по формуле D(X) = M(X 2) – M 2 (X), где
Таким образом, дисперсия дискретной случайной величины
Дисперсия имеет размерность квадрата размерности случайной величины. Поэтому для оценки рассеяния возможных значений случайной величины вокруг ее математического ожидания ее использовать неудобно. В связи с этим вводят понятие среднего квадратического отклонения, размерность которого совпадает с размерностью случайной величины. Определение. Корень квадратный из дисперсии называется средним квадратическим отклонением:
Найти числовые характеристики и построить многоугольник распределения. Решение.
Найдем числовые характеристики: 1. математическое ожидание
2. дисперсия
Определение: Функцией распределения НСВ назовем функцию

Функция Определение: Плотностью распределения НСВ назовем функцию
Функция Можно выделить основные законы распределения НСВ: 1. нормальное распределение; 2. распределение 3. распределение Стьюдента. Непрерывные случайные величины обладают следующими характеристиками: 1. математическое ожидание: 2. дисперсия: 3. среднеквадратическое отклонение: Математическая статистика.
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Пусть требуется изучить совокупность однородных объектов относительно некоторого количественного или качественного признака, характеризующего эти объекты. Выборочной совокупностью или просто выборкой называется совокупность случайно отобранных объектов. Генеральной совокупностью называется совокупность объектов, из которых производиться выборка. Наблюдаемые значения
Число наблюдений называется частотами (обозначаются
Статистическим распределением выборки называется перечень вариант и соответственно их частот (относительных частот).
Статистическое распределение можно задать так же в виде последовательности интервалов и соответствующих им частот.
Пример 1. Составит статистическое распределение и вариационный ряд следующей выборки: 2,1,1,1,3,4,2.
1,1,1,1,1,3,4 – вариационный ряд. Для оценки плотности распределения используют полигон и гистограмму частот. Полигоном частот называют ломаную, отрезки которой соединяют точки Полигоном относительных частот называют ломаную, отрезки которой соединяют точки Если признак непрерывен, то используют гистограмму частот. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частичные интервалы длиной Статистическое распределение обладает следующими числовыми характеристиками: 1. выборочная средняя 2. выборочная дисперсия 3. исправленная дисперсия 4. среднеквадратическое отклонение Доверительным называется интервал, который с заданной надежностью Для оценки математического ожидания
где
Пример 2. У семи человек продолжительность инкубационного периода вирусным гепатитом составила: 17,1; 16,2; 18,3; 16,6; 15,3; 18,6; 16,4; 16,5; 17,5; 16,9 дней. Требуется: 1) определить выборочную среднюю
Решение. 1) Определим выборочную среднюю
Выборочная средняя Выборочная дисперсия Dв Исправленная дисперсия s2 2) Полагая, что распределение признака Y описывается нормальным законом распределения, найдём доверительный интервал для средней продолжительности инкубационного периода а у обследуемых людей на уровне заданной надежности g = 0,999. Доверительный интервал найдём по формуле:
Итак,
Ответ: Выборочная средняя С надёжностью 0,999 средняя продолжительность инкубационного периода у обследуемых людей а заключена в доверительном интервале 15,45 < а < 18,43.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.29.219 (0.034 с.) |
 .
. .
. можно выносить за знак математического ожидания:
можно выносить за знак математического ожидания: .
. .
.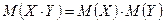 .
. .
.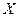 , определяемой как количество посетителей в наугад выбранной аптеке.
, определяемой как количество посетителей в наугад выбранной аптеке. = 5×0,1 +6×0,2 +7×0,3 + 8×0,3 + 9×0,1 = 7,1.
= 5×0,1 +6×0,2 +7×0,3 + 8×0,3 + 9×0,1 = 7,1.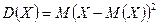 .
. .
. равна нулю:
равна нулю: .
. .
.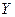 – независимые случайные величины, то
– независимые случайные величины, то .
. .
. .
. .
.

 – вероятность рождения девочки
– вероятность рождения девочки – вероятность рождения мальчика
– вероятность рождения мальчика

 3. среднеквадратическое отклонение
3. среднеквадратическое отклонение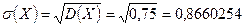



 называется интегральной.
называется интегральной.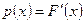
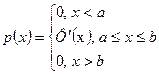


 называется дифференциальной.
называется дифференциальной. ;
;

 называются вариантами, а последовательность вариант, записанная в возрастающем порядке, называется вариационным рядом.
называются вариантами, а последовательность вариант, записанная в возрастающем порядке, называется вариационным рядом. ), а их отношение к объему выборки (обозначается
), а их отношение к объему выборки (обозначается  ) называется относительными частотами.
) называется относительными частотами.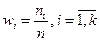







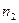



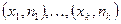 .
. .
. .
. ;
; ;
; ;
; .
. покрывает оцениваемый параметр.
покрывает оцениваемый параметр. служит доверительный интервал
служит доверительный интервал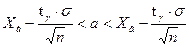
 - точность оценки,
- точность оценки,  - объем выборки,
- объем выборки,  - выборочное среднее,
- выборочное среднее,  - аргумент функции Лапласа (табличное значение).
- аргумент функции Лапласа (табличное значение). , выборочную Dв и исправленную S2 дисперсии; 2) полагая, что распределение признака Y описывается нормальным законом распределения, найдите доверительный интервал для средней продолжительности инкубационного периода а у обследуемых людей на уровне заданной надежности g = 0,999.
, выборочную Dв и исправленную S2 дисперсии; 2) полагая, что распределение признака Y описывается нормальным законом распределения, найдите доверительный интервал для средней продолжительности инкубационного периода а у обследуемых людей на уровне заданной надежности g = 0,999.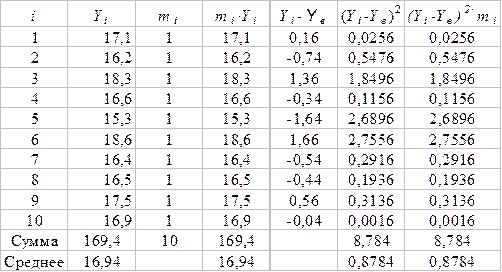
 .
. .
. .
. , где
, где 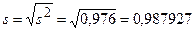 . по таблице (см. приложение 3 в [ 8 ]) по заданным n=10 g = 0,999 находим tg=4,78.
. по таблице (см. приложение 3 в [ 8 ]) по заданным n=10 g = 0,999 находим tg=4,78. и доверительный интервал
и доверительный интервал
 ; выборочная дисперсия Dв
; выборочная дисперсия Dв  ; исправленная дисперсия s2
; исправленная дисперсия s2 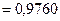 .
.


