
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки сходимости положительных рядов
Если все члены ряда имеют одинаковые знаки, то ряд называется знакопостоянным. К числу таких рядов относятся ряды, все члены которых только положительные (знакоположительные, или просто положительные ряды), и ряды, все члены которых только отрицательные (знакоотрицательные ряды). Знакоотрицательные ряды можно рассматривать как частный случай положительных, у которых все члены умножены на (–1). Положительный сходящийся ряд при перестановке членов остается сходящимся и сумма его не изменяется. Расходящийся положительный ряд при перестановке членов остается расходящимся. Сравнение положительных рядов. · 1-й признак сравнения. Пусть 1) если ряд 2) если ряд · 2-й признак сравнения (предельная форма признака сравнения). Пусть При использовании 1-го или 2-го признака сравнения, как правило, сравнивают исходный ряд с соответствующим рядом Дирихле. При этом часто используют эквивалентность следующих бесконечно малых последовательностей (при
Пример. Исследовать на сходимость ряд ◄ Применим 1-й признак сравнения. Так как
Пример. Исследовать на сходимость ряд ◄ Применим 2-й признак сравнения. Так как при
Пример. Исследовать на сходимость ряд ◄ Так как Признак Даламбера. Пусть
Пример. Исследовать на сходимость ряд
◄ Применяем признак Даламбера. Найдем предварительно отношение
Признак Коши. Пусть
Пример. Исследовать на сходимость ряд ◄ Применяем признак Коши. Найдем предварительно
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.005 с.) |
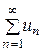 и
и 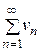 – ряды с положительными членами, причем
– ряды с положительными членами, причем  для всех номеров
для всех номеров  , начиная с некоторого. Тогда:
, начиная с некоторого. Тогда: . Тогда ряды
. Тогда ряды 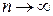 ):
):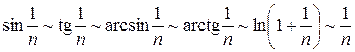 .
.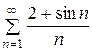 .
.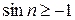 , то
, то  , откуда
, откуда 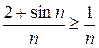 . Ряд
. Ряд  расходится, значит, расходится и больший ряд
расходится, значит, расходится и больший ряд 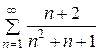 .
. (это следует из
(это следует из  ), а знаменатель
), а знаменатель 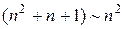 (т. к.
(т. к. 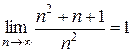 ) и, следовательно,
) и, следовательно, 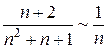 , сравним заданный ряд с гармоническим
, сравним заданный ряд с гармоническим 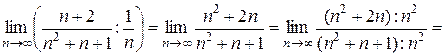 =
= 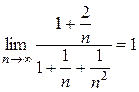 . Так как этот предел конечен и не равен нулю, а ряд
. Так как этот предел конечен и не равен нулю, а ряд 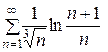 .
.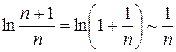 (при
(при 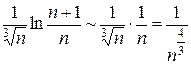 (при
(при 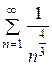 сходится (это ряд Дирихле
сходится (это ряд Дирихле 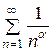 , в котором
, в котором 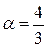 ), значит, сходится и исходный ряд. ►
), значит, сходится и исходный ряд. ► . Тогда, если
. Тогда, если 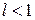 , то данный ряд сходится; если же
, то данный ряд сходится; если же 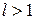 , – расходится. Если
, – расходится. Если 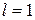 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
, то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.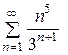 .
.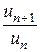 :
: 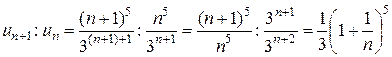 . Вычисляем предел:
. Вычисляем предел: 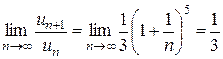 . Так как
. Так как  , исходный ряд сходится. ►
, исходный ряд сходится. ►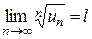 . Тогда, если
. Тогда, если 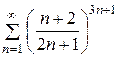 .
.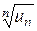 :
: 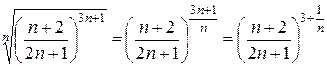 . Так как
. Так как 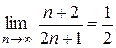 и
и 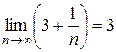 , получим
, получим 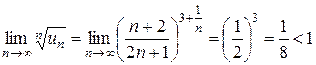 . Заданный ряд сходится по признаку Коши. ►
. Заданный ряд сходится по признаку Коши. ►


